Статья опубликована в рамках: IV Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 23 июля 2012 г.)
Наука: Информационные технологии
Секция: Системный анализ, управление и обработка информации
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АЛГОРИТМ ВОССТАНОВЛЕНИЯ ПРОПУЩЕННЫХ ДАННЫХ ПРИ ЛИДАРНЫХ ИЗМЕРЕНИЯХ ПРОФИЛЯ ВЕТРА
Баранов Николай Алексеевич
д-р. техн. наук, вед. науч. сотрудник, ВЦ РАН им. А.А. Дородницына, г. Москва
E-mail: baranov@ccas.ru
Лемищенко Екатерина Валерьевна
начальник отдела, ООО «Международные аэронавигационные системы», г. Москва
E-mail: lev@ians.aero
Сканирующий доплеровский лидар относится к средствам дистанционного измерения профиля скорости ветра ![]() , где
, где ![]() ‑ высоты сканирования,
‑ высоты сканирования, ![]() ‑ начальная высота сканирования,
‑ начальная высота сканирования, ![]() ‑ шаг сканирования по высотам,
‑ шаг сканирования по высотам, ![]() ‑ время измерения на j-й высоте,
‑ время измерения на j-й высоте, ![]() ‑ время сканирования на одной высоте,
‑ время сканирования на одной высоте, ![]() ‑ координаты точки измерений в горизонтальной плоскости. Получение полного профиля скорости ветра занимает время
‑ координаты точки измерений в горизонтальной плоскости. Получение полного профиля скорости ветра занимает время ![]() . В процессе работы возникают ситуации, когда в силу тех или иных причин на некоторых высотах в процессе одного цикла сканирования образуется пропуск данных, т.е. лидар не определяет значение скорости ветра. В этом случае возникает задача восполнения пропущенных данных измерений.
. В процессе работы возникают ситуации, когда в силу тех или иных причин на некоторых высотах в процессе одного цикла сканирования образуется пропуск данных, т.е. лидар не определяет значение скорости ветра. В этом случае возникает задача восполнения пропущенных данных измерений.
Излагаемый подход развивает подходы, изложенные в работах [1; 2; 3].
Будем представлять профиль ветра в виде суммы двух составляющих:
|
|
|
где ![]() ‑ осредненный профиль ветра, а
‑ осредненный профиль ветра, а ![]() ‑ флуктуационная составляющая скорости ветра, обусловленная турбулентными пульсациями.
‑ флуктуационная составляющая скорости ветра, обусловленная турбулентными пульсациями.
Предполагая (для упрощения изложения), что вертикальный перенос воздушных масс отсутствует, на основании гипотезы замороженной турбулентности примем допущение, что пульсационная составляющая скорости ветра ![]() на высоте h в момент времени
на высоте h в момент времени ![]() связано с ее значением в момент времени
связано с ее значением в момент времени ![]() соотношением вида
соотношением вида
|
|
|
Предположим, что на некотором цикле сканирования не были получены от лидара данные о скорости ветра ![]() на высоте
на высоте ![]() и рассмотрим задачу получения оценки
и рассмотрим задачу получения оценки ![]() этой скорости по результатам измерений скорости ветра на высотах
этой скорости по результатам измерений скорости ветра на высотах ![]() , включая измерения скорости ветра на высоте
, включая измерения скорости ветра на высоте ![]() , полученные в предыдущих циклах сканирования профиля ветра. В силу соотношения (1) задача оценивания состоит в получении оценки
, полученные в предыдущих циклах сканирования профиля ветра. В силу соотношения (1) задача оценивания состоит в получении оценки ![]() флуктуационной составляющей скорости ветра
флуктуационной составляющей скорости ветра ![]() на высоте
на высоте ![]() в момент времени
в момент времени ![]() :
:
|
|
|
Будем искать оценку ![]() в виде
в виде
|
|
|
где L – количество учитываемых циклов сканирования профиля ветра, ![]() ‑ результаты измерения на высоте
‑ результаты измерения на высоте ![]() в момент времени
в момент времени ![]() флуктуационной составляющей скорости ветра, а
флуктуационной составляющей скорости ветра, а ![]() ‑ коэффициенты интерполяции, подлежащие определению.
‑ коэффициенты интерполяции, подлежащие определению.
Будем предполагать, что ошибки измерений скорости ветра на различных высотах являются взаимно независимыми случайными величинами с нулевым математическим ожиданием и дисперсией ![]() .
.
Дисперсия ошибки аппроксимации вида (4) определяется следующим соотношением:
|
|
|
После преобразований соотношение (5) можно представить в виде
|
|
|
где значения коэффициента ![]() определяются соотношением
определяются соотношением
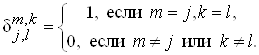
Используя необходимое условие минимума функционала (6), получаем систему уравнений для определения коэффициентов аппроксимации вида (4):
|
|
|
где
|
|
|
‑ пространственно-временная корреляционная функция пульсационных значений скорости ветра на высотах ![]() ,
, ![]() в моменты времени
в моменты времени ![]() и
и ![]() соответственно.
соответственно.
Используя принятую ранее гипотезу (2) можно перейти от пространственно-временной корреляционной функции вида (8) к пространственной корреляционной функции вида
|
|
|
приведенной к одному моменту времени ![]() .
.
В частном случае, когда используются только результаты измерений одного цикла сканирования профиля ветра, соотношение (9) принимает вид
|
|
|
В тех случаях, когда корреляционная функция ветра неизвестна в качестве приближения может быть использованы корреляционные функции компонент скорости ветра, рассчитанные на основе гипотезы однородной изотропной турбулентности.
Представим пульсационные составляющие скорости ветра в виде суммы двух составляющих: продольной и нормальной проекции скорости ветра на радиус-вектор, соединяющий две точки измерения на разных высотах (рис. 1):
![]() ,
,
где ![]() ‑ единичный вектор, соответствующий направлению от точки
‑ единичный вектор, соответствующий направлению от точки ![]() , а
, а ![]() ‑ единичный вектор нормали к нему.
‑ единичный вектор нормали к нему.
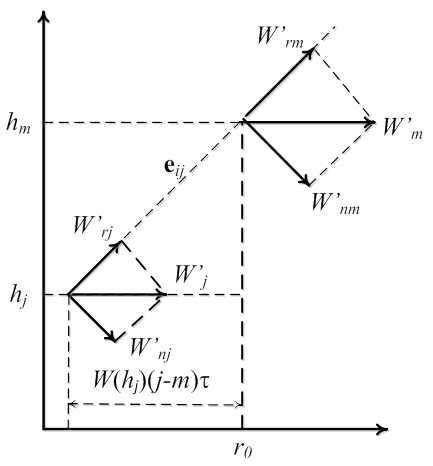
Рисунок 1. Разложение скорости ветра на продольную и нормальную составляющие
Тогда корреляционную функцию (9) можно представить в виде
|
|
|
Первое слагаемое в этом выражение представляет собой корреляционную функцию радиальных компонент вектора скорости (направленных вдоль радиус-вектора, соединяющего точки ![]() и
и ![]() ), а второе – корреляционную функцию компонент вектора скорости, нормальных к направлению
), а второе – корреляционную функцию компонент вектора скорости, нормальных к направлению ![]() (рис. 1).
(рис. 1).
В рамках предположения об однородной изотропной турбулентности эти корреляционные функции зависят только от расстояния между точками
![]()
и имеют вид
![]()
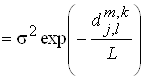 ,
,
![]()
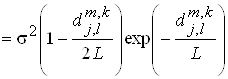 ,
,
где ![]() – среднеквадратическое отклонение скорости ветра, L – масштаб турбулентности. В частном случае, когда для восстановления данных используются результаты только одного цикла сканирования профиля ветра выражение для
– среднеквадратическое отклонение скорости ветра, L – масштаб турбулентности. В частном случае, когда для восстановления данных используются результаты только одного цикла сканирования профиля ветра выражение для ![]() принимает вид
принимает вид
![]() .
.
Таким образом, в рамках предположения об однородной изотропной турбулентности система уравнений (7) для определения коэффициентов аппроксимации пульсационной составляющей скорости ветра в пропущенных данных принимает вид
|
|
|
Работа выполняется при финансовой поддержке РФФИ (проекты № 10-07-00381, 12-07-00697) и программы фундаментальных исследований ОМН РАН № 3.
Список литературы:
1.Баранов Н.А., Васильев И.В. Восстановление возмущающего воздействия для многомерных динамических систем. // Информационно-измерительные и управляющие системы. 2008. Т. 6. № 7. С. 40 — 46.
2.Баранов Н.А., Васильев И.В., Шаповалов Н.Н. Алгоритмы восстановления возмущающего воздействия. // Информационно-измерительные и управляющие системы. 2007. Т. 5. № 8. С. 32 — 38.
3.Baranov N.A. Improving the scanning lidar wind speed measurement accuracy by using the optimal interpolation //European researcher = Европейский исследователь. 2012. Т. 1. № 5. С. 432 — 435.
дипломов

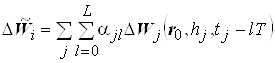 ,
,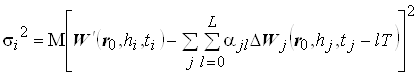 .
.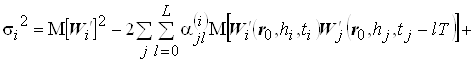
 ,
,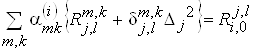 ,
,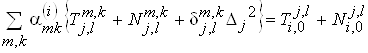 .
.
Оставить комментарий