Статья опубликована в рамках: III Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 11 июня 2012 г.)
Наука: Физика
Секция: Теоретическая физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
В каком ящике находятся операции симметрии пространства Минковского?
Обратная задача первого типа
Бадретдинов Явит Сафтдинович
доцент, канд. пед. наук, доцент кафедры общей физики, БирГСПА, г. Бирск
E-mail: jsbadr@rambler.ru
«Важны не вещи, а принципы симметрии»
Стивен Вайнберг
Введение
Принципы симметрии, куда непременно входят и операции симметрии в пространстве М, сыграли, как известно [2], решающую роль в построении теории электрослабого взаимодействия. Создание единой теории всех сил, в том числе и гравитации, как полагает ряд физиков [7, с. 201], также связано с операциями симметрии, но уже не четырехмерного, а одиннадцатимерного пространства. Таким образом, представления о симметрии пространства в комбинации с динамическими симметриями взаимодействующих частиц выступают на первый план в познании единой картины мира. В этой связи выявление всех свойств симметрии пространства, в том числе и пространства М, представляет собой актуальную физическую задачу. Поскольку свойства симметрии пространства М связаны с операциями симметрии, то возникает вопрос, существует ли теория, позволяющая вывести из одного закона, т.е. следуя М. Планку «из единственной формулы» [6, c. 23], известные операции симметрии, а также найти новые операции симметрии в пространстве М. В настоящее время в физике такой теории нет, ибо, как было отмечено В. Паули [5, c. 24] и Е. Вигнером [1, c. 10, 65], операции симметрии в пространстве М постулированы, т. е. они интуитивно угаданы. Сказанное верно как в отношении непрерывных операций симметрии в пространстве М (сдвиг и поворот), так и дискретных операций симметрии (зеркальное отражение или инверсия). Ввиду того, что дискретные операции симметрии в пространстве М связаны с дискретными преобразованиями Лоренца, то нет ответа и на вопрос, сколько дискретных преобразований координат допускается в пространстве М.
Ответы на поставленные выше, а также и другие вопросы применительно к пространству М можно получить путем постановки и решения обратных задач трех типов.
Обратная задача первого типа. Найти уравнения пространства М из требования инвариантности волнового уравнения электродинамики.
Уравнения пространства М мы будем рассматривать как физический закон, отражающий сущность пространства М в форме соответствующих дифференциальных уравнений, представляющих собой как бы «ящик», в который и «встроены» все операции симметрии пространства М.
Обратная задача второго типа. Найти один вариант непрерывных комплексно-сопряженных решений уравнений пространства М и вывести из них как следствия все непрерывные операции симметрии в действительном и комплексном пространствах М.
Обратная задача третьего типа. Найти все варианты дискретных комплексно-сопряженных решений уравнений пространства М и вывести из них как следствия все дискретные операции симметрии в действительном и комплексном пространствах М.
Таким образом, обратные задачи второго и третьего типа и методы их решения дают как бы ключ, с помощью которого «открываются» уравнения пространства М как «ящик», откуда и «вынимаются» все операции симметрии пространства М.
1.Обратная задача первого типа. Вывод уравнений пространства М из волнового уравнения электродинамики
Смысл вышеприведенных обратных задач становится более понятным, если мы знаем как формулируется прямая задача применительно к нашему случаю. Прямая задача была решена Лоренцом [8]. Он показал, что волновое уравнение электродинамики остается неизменным относительно найденных им преобразований, т. е. преобразований Лоренца. Обратная задача – найти преобразования Лоренца из условия инвариантности волнового уравнения электродинамики, по-видимому, не поставлена до настоящего времени. Эту задачу, как выше было показано, мы делим на три задачи: обратная задача первого, второго и третьего типа.
Обратная задача первого типа. Из требования инвариантности волнового уравнения электродинамики вывести в соответствии с принципом относительности уравнения пространства М. В качестве иллюстрации, подтверждающей функцию принципа инвариантности в установлении нового закона, можно привести закон сохранения импульса. Если бы закон сохранения импульса не был известен, то его можно было бы вывести из условия инвариантности закона сохранения энергии относительно преобразований Галилея. В случае же уравнений пространства М ситуация аналогична. Уравнения пространства М как бы «вложены» в волновое уравнение электродинамики и их можно оттуда «вытащить», используя в соответствии с принципом относительности процедуру инвариантности, а точнее, следуя А.А. Логунову форминвариантности [4, c. 11, 20], в отношении волнового уравнения. Вышесказанное представляет собой частный случай утверждения, которое, следуя Е. Вигнеру, можно сформулировать так: в ряде случаев «удается найти новые законы природы на основе постулата о том, что законы должны обладать определенной инвариантностью» [1, с. 36]. Переходим к выводу уравнений пространства М. С целью простоты рассуждений рассмотрим двумерный случай.
В инерциальных системах отчета ![]() и
и ![]() волновое уравнение в галилеевых координатах имеет вид:
волновое уравнение в галилеевых координатах имеет вид:
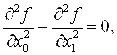 (1)
(1)
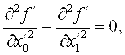 (2)
(2)
где ![]() и
и ![]() – скалярные функции в пространстве М, причем
– скалярные функции в пространстве М, причем ![]() ;
; ![]() ;
; ![]() – время и декартовые координаты точки в системах отсчета
– время и декартовые координаты точки в системах отсчета ![]() и
и ![]() ;
; ![]() – электродинамическая постоянная. Искомые преобразования представим в виде
– электродинамическая постоянная. Искомые преобразования представим в виде
![]() (3)
(3)
С учетом (3) находим первые и вторые производные от ![]() по
по ![]() :
:
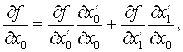
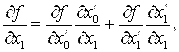
 (4)
(4)
После подстановки (4) в (1) получим
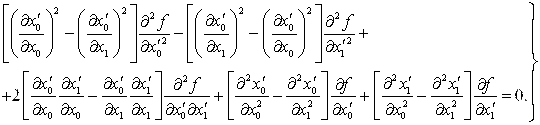 (5)
(5)
Уравнение (5) в соответствии с требованием форминвариантности перейдет в уравнение (2) при выполнении следующих условий:
 (6)
(6)
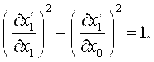 (7)
(7)
 (8)
(8)
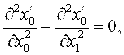 (9)
(9)
 (10)
(10)
Систему уравнений ((6)-(10)) применительно к четырехмерному случаю обобщенно можно представить так:
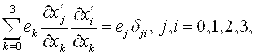 (11)
(11)
 (12)
(12)
где 
Уравнения (11) и (12) соответствуют преобразованиям координат при переходе от системы отсчета ![]() к
к ![]() . Столько же уравнений получим при обратном переходе, т.е. от
. Столько же уравнений получим при обратном переходе, т.е. от ![]() к
к ![]()
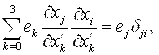 (13)
(13)
 (14)
(14)
Полученные уравнения (11) и (12), или (13) и (14) назовем уравнениями пространства М.
2.Анализ уравнений пространства М
Закон о пространстве в форме дифференциальных уравнений
Уравнения ((11)-(12)), как выше было сказано, представляют собой уравнения пространства. Это означает, что эти уравнения как физический закон выражают сущность пространства М в форме дифференциальных уравнений, подобно тому как уравнения Максвелла в качестве физического закона выражают сущность электродинамики. Утверждение о том, что уравнения пространства представляют собой физический закон, доказывается с применением процедуры инвариантности в отношении уравнений пространства М. Предварительный ответ таков: уравнения пространства М удовлетворяют требованию инвариантности, тогда эти уравнения приобретают статус физического закона. Докажем этот результат. Подвергнем процедуре инвариантности только два уравнения (6) и (8). В случае перехода от системы отчета ![]() к
к ![]() имеем
имеем
![]() (15)
(15)
Уравнения (6) и (8) для этого случая имеют вид:
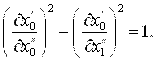 (16)
(16)
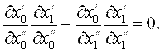 (17)
(17)
Здесь в соответствии с требованием инвариантности уравнения (6) и (8) в ходе преобразований (15) должны переходить в уравнения (16) и (17). Находим первые производные от ![]() и
и ![]() (см. (15)) по
(см. (15)) по ![]() :
:
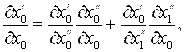 (18)
(18)
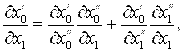 (19)
(19)
 (20)
(20)
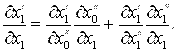 (21)
(21)
После подстановки (18) и (19) в (6) получим
 (22)
(22)
После подстановки (20) и (21) в (8) имеем
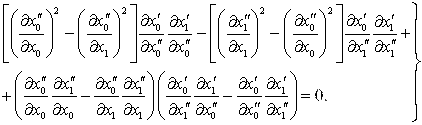 (23)
(23)
В соответствии с требованием инвариантности уравнение (22) переходит в уравнение (16), а уравнение (23) в уравнение (17) при выполнении следующих условий:
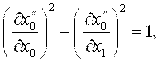 (24)
(24)
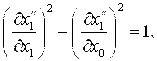 (25)
(25)
 (26)
(26)
Уравнения ((24)-(26)) представляют собой уравнения пространства М, соответствующие переходу от системы отчета ![]() к
к ![]() , т.е.
, т.е. ![]() ,
, ![]() . Таким образом, уравнения пространства ((6)—(10)) удовлетворяют требованию инвариантности, следовательно, эти уравнения ((6)—(10)) приобретают статус физического закона. Кроме того, отметим еще один важный результат: применение процедуры инвариантности к каждому уравнению пространства генерирует уравнения пространства ((24)—(26)). Другими словами, каждое уравнение пространства М потенциально содержит сущность пространства подобно тому, как любой осколок голограммы содержит всю информацию об объекте.
. Таким образом, уравнения пространства ((6)—(10)) удовлетворяют требованию инвариантности, следовательно, эти уравнения ((6)—(10)) приобретают статус физического закона. Кроме того, отметим еще один важный результат: применение процедуры инвариантности к каждому уравнению пространства генерирует уравнения пространства ((24)—(26)). Другими словами, каждое уравнение пространства М потенциально содержит сущность пространства подобно тому, как любой осколок голограммы содержит всю информацию об объекте.
3.Доказательство линейности преобразований координат ![]() в пространстве М
в пространстве М
В геометрической теории пространства линейность преобразований галилеевых координат не доказывается, а чаще всего постулируется, или для объяснения линейности ![]() используется вывод из другой физической теории, а именно из механики: равномерное и прямолинейное движение в системе отчета
используется вывод из другой физической теории, а именно из механики: равномерное и прямолинейное движение в системе отчета ![]() должно быть таким же и в
должно быть таким же и в ![]() [5, c. 24]. Мы же исходим из того, что теория пространства должна дать ответы на все вопросы, относящиеся к пространству, в том числе и на вопрос, какими должны быть преобразования
[5, c. 24]. Мы же исходим из того, что теория пространства должна дать ответы на все вопросы, относящиеся к пространству, в том числе и на вопрос, какими должны быть преобразования ![]() .
.
Выпишем для двумерного случая уравнения пространства М первого типа (см. (6)-(8))
 (27)
(27)
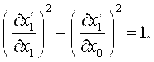 (28)
(28)
 (29)
(29)
Решения уравнений (27) и (28) будем искать в виде:
 (30)
(30)
Возьмем один вариант искомых решений (30) со знаком ![]() и подставим в (29), что дает
и подставим в (29), что дает
![]()
или
![]()
или
![]() (31)
(31)
Уравнения (30) (с учетом (31)) пока не сможем интегрировать, так как ![]() представляет собой неизвестную функцию. Явный вид
представляет собой неизвестную функцию. Явный вид ![]() найдем из условия интегрируемости функций
найдем из условия интегрируемости функций ![]() и
и ![]() :
:
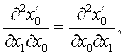 (32)
(32)
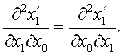 (33)
(33)
Подстановка (30) (со знаком ![]() в правой части и с учетом (31)) в (32) и (33) дает
в правой части и с учетом (31)) в (32) и (33) дает
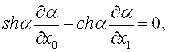 (34)
(34)
 (35)
(35)
Уравнения (34) и (35) представляют собой систему двух однородных линейных уравнений относительно ![]() и
и ![]() с определителем, отличным от нуля и равным единице, т.е.
с определителем, отличным от нуля и равным единице, т.е.
![]()
Это значит, что уравнения (75) и (76) имеют только тривиальные решения [3, c. 47]:


откуда
![]() (36)
(36)
Тогда решения уравнений (30) для одного варианта (в правой части берется знак ![]() ) имеет следующий вид:
) имеет следующий вид:
![]()
![]()
Следовательно, решения уравнений пространства М ((27)-(29)), взятых в декартовых координатах, представляют собой линейные преобразования, т. е. ![]() и
и ![]() линейно зависят от
линейно зависят от ![]() и
и ![]() . Верно и обратное утверждение. Кроме того, результат (36) позволяет сформулировать ещё один вывод: уравнения пространства М ((27)-(29)) относительно
. Верно и обратное утверждение. Кроме того, результат (36) позволяет сформулировать ещё один вывод: уравнения пространства М ((27)-(29)) относительно ![]() представляют собой систему алгебраических уравнений.
представляют собой систему алгебраических уравнений.
Список литературы:
1.Вигнер Е. Этюды о симметрии: Пер. с англ. / Под ред. Я.А. Смородинского. –М.: Мир, 1971. –318 с.
2.Глэшоу Ш., Салам А., Вайнберг С. Нобелевские лекции по физике // УФН, –1980. т. 132, вып. 2.
3.Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. –М.: Наука. Гл. ред. физ.-мат. лит., 1973. –831 с.
4.Логунов А.А. Лекции по теории относительности и гравитации: Современный анализ проблемы. –М.: Наука. Гл. ред. физ.-мат. лит., 1987. –272 с.
5.Паули В. Теория относительности: Пер. с нем. и англ. – 3-е изд. испр. / Под ред. В.Л. Гинзбурга и В.П. Фролова. –М.: Наука. Гл. ред. физ.-мат. лит., 1991. (Б-ка теор.физики). –328 с. – ISBN 5-02-014346-4.
6.Планк М. Единство физической картины мира. –М.: Наука, 1966. – 288 с.
7.Салам А. Унификация сил // Фундаментальная структура материи/ Пер. с англ.: под ред. и с предел. А.Д. Суханова. –М.: Мир, 1984. С. 173—203.
8.Lorentz H.A. Electromagnetic Phenomena in a System Moving with any Velocity Smaller than that of Light // Amst. Proc. – V. 6. – P. 809; 1904. V. 12. – P. 986.
дипломов

Оставить комментарий