УСЛОВИЯ ВОЗНИКНОВЕНИЯ ОТКЛИКОВ ДВУХУРОВНЕВОЙ СИСТЕМЫ НА ВОЗДЕЙСТВИЕ ОДНОГО РЕЗОНАНСНОГО ЛАЗЕРНОГО ИМПУЛЬСА И ДВУХ НЕРЕЗОНАНСНЫХ ЭЛЕКТРОМАГНИТНЫХ СТОЯЧИХ ВОЛН

Гузель Ильдаровна Гарнаева

канд. физ.-мат. наук, доцент, Казанский (Приволжский) Федеральный университет (кафедра образовательных технологий в физике), г. Казань

e-mail: guzka-1@yandex.ru

Леонид Анатольевич Нефедьев

д-р физ.-мат. наук, профессор, Казанский (Приволжский) Федеральный университет (кафедра образовательных технологий в физике), г. Казань

e-mail: nefediev@yandex.ru

Екатерина Николаевна Ахмедшина

аспирант, Казанский (Приволжский) Федеральный университет (кафедра образовательных технологий в физике), г. Казань

e-mail: vesnuschka-88@yandex.ru,

Эльза Ильдаровна Хакимзянова

аспирант, Казанский (Приволжский) Федеральный университет (кафедра образовательных технологий в физике), г. Казань

e-mail: Elzahakim@yandex.ru

В работе [1] была показана возможность управления временем появления штарковского эха путем варьирования величин приложенных градиентов внешних пространственно неоднородных электрических полей или их взаимной ориентации. Аналогичного эффекта можно добиться с помощью нерезонансных взаимодействий системы с лазерными полями. Нерезонансные явления связаны с виртуальными переходами атомного электрона. Различие между виртуальными и реальными переходами определяется временем жизни τ атома в промежуточном состоянии. В случае реальных переходов время жизни определяется вероятностью перехода атомного электрона из данного состояния. В случае виртуальных переходов понятие времени жизни возникает из соотношения неопределенности ΔEτ~ħ, где роль неопределенности в энергии играет расстройка от резонанса ΔE=ħ(ω_ns-ω), где ω – несущая частота лазерного излучения, а ω_ns – частота перехода между связанными состояниями n и s.

После включения взаимодействия с нерезонансным лазерным излучением волновая функция n-го состояния атома

,

где коэффициенты a_s малы, а ǀa_nǀ→1. Таким образом сдвиг энергии n-го состояния δE<<ħω_ns. Чтобы не учитывать изменение волновой функции атома после воздействия нерезонансного лазерного возмущения, необходимо, чтобы время жизни промежуточных виртуальных состояний τ было гораздо меньше рассматриваемых временных интервалов при формировании штарковского эха. В случае, если нерезонансные лазерные поля имеют пространственную неоднородность, то сдвиги энергии δЕ становятся функциями координат δЕ(r), что приводит к возникновению дополнительного неоднородного уширения резонансного перехода в образце.

Работа посвящена теоретическому исследованию особенностей формирования откликов двухуровневой квантовой системы при воздействии одного резонансного лазерного импульса и двух нерезонансных электромагнитных стоячих волн.

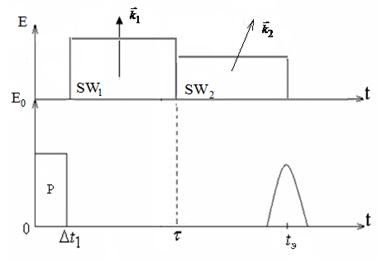
Рис. 1. Схема возбуждения градиентного (штарковского) эха. Р – возбуждающий лазерный импульс, SW₁, SW₂ – импульсы нерезонансных стоячих волн лазерного излучения, t_э – время появления отклика штарковского эха, Δt₁ – длительность возбуждения резонансного лазерного импульса.

Рассмотрим схему возбуждения двухуровневой системы последовательностью одного резонансного лазерного импульса и двух нерезонансных лазерных импульсов, образующих стоячие волны (рис. 1). Время воздействия первого нерезонансного лазерного импульса будем считать равным τ, а время второго - до момента появления отклика системы. Для уменьшения затухания из-за обратимой релаксации Т₂^* будем полагать область возбуждения неоднородно уширенной линии резонансными лазерными импульсами равной 2kσ, где k<<1, σ – ширина неоднородно уширенной линии. Уравнение для одночастичной матрицы плотности во вращающейся системе координат запишем в виде

,                                                                     (1)

где

,

,

,

A - матрица перехода во вращающуюся систему координат, U - оператор взаимодействия резонансной системы с возбуждающим лазерным импульсом, H_0m - гамильтониан атома во внешнем пространственно неоднородном нерезонансном лазерном излучении на τ_m-ом временном интервале, r - радиус-вектор местоположения атома. В случае двухуровневой системы A=P₂₂ω₁₂.

Решение уравнения (1) для двухуровневой системы было получено в работе [2]. Фазовая часть напряженности электрического поля отклика системы в этом случае имеет вид

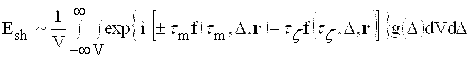,                    (2)

где f(τ_m,Δ,r)=Δ+ε(τ_m,Δ,r) - полные частотные сдвиги уровней резонансных атомов, V - объем возбуждаемой части образца, Δ – сдвиг отдельной монохроматы, g(Δ) - Гауссова функция распределения частот, соответствующая ширине лазерного возбуждения неоднородно уширенной линии резонансного перехода 2kσ, С_D – постоянная динамического эффекта Штарка, E_0m - амплитуда напряженности электрического поля m-го нерезонансного лазерного импульса.

Рис. 2. Временная форма отклика при τ=10нс, α=0, γ=0, β=75⁰

При сравнении частотных сдвигов оптических центров на разных временных интервалах  за счет взаимодействия с различно пространственно ориентированными стоячими волнами, удобно задать вектор  в системе координат , связанной с направлением распространения лазерного излучения:

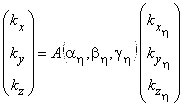
                                                      (3)

где  - орты системы координат . Тогда в лабораторной системе координат

                                                    (4)

где A - матрица вращений. Из (4) следует, что

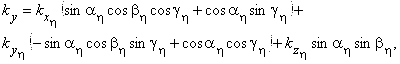
Здесь ,  и  - углы Эйлера, определяющие взаимную ориентацию систем координат  и .

На рисунке 2 приведена форма отклика системы, которая возникает при определенных углах ориентации стоячих волн и значении k=0,01. Таким образом, наблюдается новый тип фотонного эха, формирование которого связано с пространственной структурой нерезонансных лазерных импульсов в качестве которых берутся стоячие волны. Такой тип откликов наблюдается только при определенных углах взаимной ориентации этих полей, что отличает его как от обычных сигналов фотонного эха, так и сигналов Штарковского эха.

Список литературы:

1.Нефедьев Л.А., Гарнаева Г.И., Хакимзянова Э.И.. Особенности формирования штарковского эха при различных величинах градиентов внешних неоднородных электрических полей // Оптический журнал. 2011. Т. 78. № 6. С. 355—357

2.Нефедьев Л.А., Гарнаева (Хакимзянова) Г.И. Эффект «запирания» сигналов фотонного эха при многоканальной записи информации // Оптика и спектроскопия. 2008. Т. 105. № 6. С. 1007—1012