Статья опубликована в рамках: III Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 11 июня 2012 г.)
Наука: Физика
Секция: Механика жидкости, газа и плазмы
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Горение ПРОПАНО-воздушной смеси между двумя зданиями
Хамидуллин Ильдар Раифович
канд. физ.-мат. наук, ст. преп., НФ БашГУ, г. Нефтекамск
E-mail:
1. Введение. Природный газ при нормальных условиях имеет большой удельный объем, поэтому хранение и транспорт осуществляется при высоких давлениях. Это значительно повышает вероятность аварийных ситуаций. Численное моделирование процессов выбросов углеводородов с последующим возгоранием является наиболее рациональным и распространенным методом, которое позволяет проводить прогнозирование последствий, оценку ущерба и разработку мер защиты.
2. Основные уравнения. Рассмотрим облако как смесь газов, которое принимается за гомогенную среду с плотностью ρ, температурой T, давлением p. Пусть ![]() скорость этой среды, определяемая как среднемассовая скорость составляющих
скорость этой среды, определяемая как среднемассовая скорость составляющих
![]() . (1)
. (1)
Введем среднемассовые концентрации каждой компоненты смеси ![]() . Здесь и в дальнейшем индексы i = 1, … , 6 будут соответствовать углеводороду, кислороду, углекислому газу, водяному пару, окиси углерода и азоту. Эти значения концентраций удовлетворяют условию
. Здесь и в дальнейшем индексы i = 1, … , 6 будут соответствовать углеводороду, кислороду, углекислому газу, водяному пару, окиси углерода и азоту. Эти значения концентраций удовлетворяют условию
![]() . (2)
. (2)
Для смеси газов выполняется закон Дальтона, и для определения давления смеси используем уравнение Менделеева-Клапейрона
![]() ,
, ![]() . (3)
. (3)
На основе принятых предположений можем записать систему, описывающую динамику облака газов, в которую входят уравнения неразрывности, диффузии, импульсов для всей смеси и уравнение теплового баланса:
![]() , (4)
, (4)
 , (5)
, (5)
![]() , (6)
, (6)
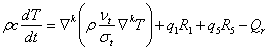 . (7)
. (7)
Удельная теплоемкость смеси определяется через удельные теплоемкости компонент
![]() . (8)
. (8)
Для более детального описания процессов тепломассопереноса к данной системе уравнений (3)—(7) добавляются дополнительные уравнения ![]() модели
модели
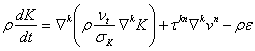 , (9)
, (9)
 , (10)
, (10)
![]() . (11)
. (11)
Скорость реакции определяется температурой смеси через соотношения Аррениуса. Согласно данной схеме учитываются следующие процессы:
![]() ,
, ![]() , 14)
, 14)
![]() ,
, ![]() . 15)
. 15)
Концентрации окисей водорода и азота для рассматриваемых смесей ~1 %. Поэтому, уравнение масс для них имеет вид
![]() . (16)
. (16)
Образование и исчезновение OH и NO сопровождается тепловыми эффектами
![]() .
.
Скорость реакции горения углеводорода определяется согласно закону Аррениуса как [2, с. 53]
![]() . (17)
. (17)
Реакция горения окиси углерода обратима, поэтому скорости прямой и обратной реакции выражаются соотношениями
![]() ,
, ![]() . (18)
. (18)
Скорости изменения концентраций ![]() ,
, ![]() и
и ![]() определяются как
определяются как
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Константы реакций диссоциации и рекомбинации (15) имеют вид
|
|
|
|
|
3. Начальные и граничные условия. Расчетная область ограничена 6 плоскими границами. Верхняя и боковые границы являются открытыми, и на них для параметров задаются фоновые значения. Нижняя граница является закрытой, и на ней скорость равна нулю. Для удобства задания начальных условий на прямоугольной сетке примем исходную форму облака в виде куба.
В начальный момент времени температуры окружающего воздуха и пропана однородны во всей расчетной области, давление определяется распределением Больцмана. Скорость движения в начальный момент времени равна нулю во всей расчетной области.
4. Численная схема. Численная схема решения системы уравнений (3)—(11), (16) основана на методе крупных частиц [1, с. 52—84]. К преимуществам данного метода относится устойчивость в широком диапазоне скорости движения среды.
5. Результаты расчетов. Рассмотрим случай залпового выброса пропана в простейшей конфигурации строений – в городском каньоне, образованном двумя зданиями, расположенными симметрично относительно центра выброса (рис. 1). Для анализа последствий горения образовавшейся смеси рассмотрим момент зажигания ![]() =30 с.
=30 с.
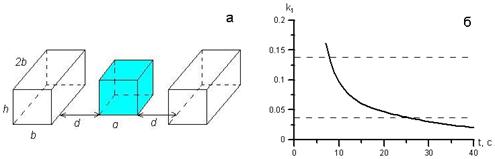
Рисунок 1 – Перемешивание залпового выброса пропана с окружающим воздухом: а – конфигурация строений и начального положения облака, б – эволюция значения среднемассовой концентрации пропана в центре облака на высоте 0,5 м.
На рис. 2, а представлены конфигурации зон теплового и разрушительного воздействия около земли, границы которых определены как огибающая площади, в которой в течение всего процесса горения температура и давление превысили критические значения (![]() =1000 К,
=1000 К, ![]() =1,1 атм).
=1,1 атм).
На рис. 2, б и 2, в представлены расчетные осциллограммы для ряда характерных точек, указанных на рис. 2, а. Значения температуры в каньоне между зданиями (точки 1,2,3) достигают величин порядка 1800 К и превышают ![]() в течение 1.5—3 с. Значение температуры за зданием (точка 4) повышается незначительно (
в течение 1.5—3 с. Значение температуры за зданием (точка 4) повышается незначительно (![]() =20 К) и, по-видимому, только за счет конвективного переноса тепла из очага горения. Пиковые значения давления в каньоне (точки 1,2,3) достигают значения 1,06
=20 К) и, по-видимому, только за счет конвективного переноса тепла из очага горения. Пиковые значения давления в каньоне (точки 1,2,3) достигают значения 1,06![]() . Колеблющийся характер давления объясняется отражением от стен строений. Также сравнивая величины давления в точках 1 и 2 можно утверждать об усиливающей роли стен зданий. Величина давления в точке 4 не превышает критических значений, при которых может произойти разрушение.
. Колеблющийся характер давления объясняется отражением от стен строений. Также сравнивая величины давления в точках 1 и 2 можно утверждать об усиливающей роли стен зданий. Величина давления в точке 4 не превышает критических значений, при которых может произойти разрушение.
Таким образом, результаты расчетов позволяют определить детальную картину полей температур и давлений в очаге горения в городском каньоне и получить количественную оценку разрушительного действия пожаров.

Рисунок 2 – Горение пропано-воздушного выброса между двумя зданиями при ![]() = 30 с: а – зоны теплового (штриховая) и силового (сплошная) воздействия; б, в – эволюция температуры (б) и давления (в) в характерных точках расчетной области (1 – сплошная, 2 – штриховая, 3– штрих-пунктирная, 4 – штрих-трехпунктирная).
= 30 с: а – зоны теплового (штриховая) и силового (сплошная) воздействия; б, в – эволюция температуры (б) и давления (в) в характерных точках расчетной области (1 – сплошная, 2 – штриховая, 3– штрих-пунктирная, 4 – штрих-трехпунктирная).
Список литературы:
1.Белоцерковский, О.М., Давыдов, Ю.М. Метод крупных частиц в газовой динамике. – М.: Наука, 1982. – 392 с.
2.Smirnov, N.N., Nikitin, V.F., Legros, J.C. Ignition and combustion of turbulent dust-air mixtures. // Combustion and Flame. 2000. V. 123. P. 46—67.
дипломов

Оставить комментарий