АНАЛИЗ МОДЕЛЕЙ ОБЪЕКТОВ РАЗЛИЧНЫХ ПРЕДМЕТНЫХ ОБЛАСТЕЙ, СВОДИМЫХ К ПОЛИНОМИАЛЬНОЙ МОДЕЛИ СО СТЕПЕНЯМИ ПЕРЕМЕННЫХ ПО МОДУЛЮ НЕ ПРЕВЫШАЮЩИМИ ЕДИНИЦУ

Петров Андрей Юрьевич

аспирант, Северо-Кавказский горно-металлургический институт (государственный технологический университет), г. Владикавказ

E-mail: Andrey.Y.Petrov@gmail.com

Существует множество систем управления и обработки информации, особенности функционирования которых формально могут быть представлены математической моделью следующего вида:

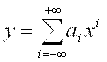                                                                               1

где    – i-й коэффициент модели;

 – переменная модели в степени i, представляет собой параметр, значение которого следует установить.

Фактическое количество слагаемых в (1) определяется семантикой задачи, исходя из специфики области приложения, требованиями к точности промежуточных и итоговых результатов, доступными в контексте данной задачи ресурсами, конкретными ограничениями, установленными на некоторые операции.

Среди объектов, описываемых с помощью (1) можно выделить достаточно широкий класс систем управления и обработки информации, для описания которых используются полиномиальные модели, степень переменных которых по модулю не превышают единицу. Конкретные формальные постановки задач оптимизации параметров систем подобного класса могут отличаться принятыми ограничениями, устанавливающими связь между переменными, условиями изменения переменных, векторами переменных [1]. Однако главным интегрирующим свойством систем, принадлежащим данному классу, является единство сущности целевых функций формальных постановок, которая заключается в наличии двух слагаемых компонент следующей семантики (в предположении, что формальная постановка содержит единственную переменную):

1)  первая компонента представляет собой составляющую выходной величины, значение которой возрастает при увеличении значения переменной;

2)  второй компонента соответствует составляющей выходной величины, значение которой убывает при увеличении значения переменной;

Каждая рассмотренная компонента полиномиальной модели описывает некоторый процесс системы, протекание которого вызывает определенное изменение выходной величины, что описывается функциональной зависимостью. Так как действие этих процессов оказывает противоположное влияние на изменение выходной величины, системы, описываемые полиномиальными моделями указанного вида, характеризуются еще одним общим свойством: в их функционировании присутствуют два взаимно обратных процесса, вызывающие взаимно обратное изменение выходной величины. Помимо приведенных двух компонент, формирующих выходную величину, можно выделить также одну необязательную компоненту, представляющую собой постоянную, которая в частном случае может быть принята равной нулю.

На практике достаточно часто встречаются системы, функционирование которых отражают два противоположных процесса при единственной переменной: один процесс выражается прямо пропорциональной зависимостью от переменной, другой – обратно пропорциональной. В качестве примеров ситуации, в которой протекают два рассмотренных процесса можно выделить следующие: задача выбора значения частоты запуска антивирусного сканера; определение оптимального количества процессоров при параллельной обработки информации; задача о замене оборудования.

Несмотря на многообразие различных технологий антивирусной защиты, на практике большинство из них основывают свою работу или так или иначе связывают ее с принципом сканирования объектов. При этом следует обратить особое внимание на необходимость оптимизации процесса управления антивирусными программными продуктами, реализующими технологию сканирования. Известно, что общие затраты времени на обеспечение информационной безопасности за фиксированный контрольный период работы ЭВМ зависят от периода между запусками антивирусного сканера [3, 4]. Задача оптимизации функционирования антивирусных сканеров характеризуется двумя противоположными процессами, действие которых оценивается за определенный интервал времени работы компьютера:

1)  снижение общих затрат времени на поиск вредоносных объектов в информационном массиве при увеличении периода между запусками антивирусного сканера;

2)  увеличение общих затрат времени на восстановление поврежденных данных с ростом периода между запусками антивирусного сканера.

В результате, системы управления и обработки данных, область приложения которых связана с организацией оптимальной работы антивирусного сканера могут быть описаны полиномиальными моделями.

Не меньшую актуальность имеет проблема определения количества процессоров многопроцессорного вычислительного устройства (МВУ), минимизирующих стоимость решения задачи или ряда задач, в заданных условиях [2]. Понятие МВУ включает в себя ЭВМ, содержащую многоядерные процессоры; многопроцессорный вычислительный комплекс; многопроцессорные видеоплаты; компоненты облачных технологий и т. п. Пусть МВУ используется для решения одной конкретной задачи. Очевидно, что с увеличением числа процессоров или процессорных элементов, задействованных для решения данной задачи, время ее решения падает. Однако при этом стоимость материальной базы (вычислительного устройства) возрастает пропорционально количеству используемых процессоров, в первом приближении линейно.

Таким образом, в системах оптимизации параллельной обработки данных, ориентированных на минимизацию стоимости решения задач, имеют место два противоположных процесса:

1)  прямой процесс связан с возрастанием оценочной стоимости решения задач при увеличении числа процессоров, что обусловлено финансовыми затратами на приобретение соответствующего аппаратного обеспечения;

2)  обратный процесс заключается в падении оценочной стоимости решения задач при увеличении числа процессоров за счет снижения общего времени решения задач с помощью МВК.

В процессе эксплуатации оборудования некоторого типа (тип определяется областью приложения) возникает его естественный износ, который требует текущего ремонта по истечении некоторого промежутка времени его работы. В случае продолжения эксплуатации оборудования затраты на текущий ремонт, обслуживание, а также на некоторые специфические компоненты, формирующие стоимость владения, возрастают с течением времени. Зависимость стоимости эксплуатации оборудования от времени его работы в первом приближении может выражаться линейной функцией. Обратный процесс заключается в том, что собственная стоимость оборудования постепенно снижается в процессе эксплуатации и в первом приближении стоимость эксплуатируемого оборудования находится в обратно пропорциональной зависимости от времени его работы. Скорость изменения собственной стоимости зависит от многих факторов, основными из которых являются динамика развития отрасли, потребность рынка в модернизации и совершенствовании существующих моделей оборудования, условия эксплуатации. Таким образом, по истечении определенного периода эксплуатации оборудования затраты на обслуживание начинают превышать собственную стоимость приобретенного оборудования на данный момент времени. Рассмотренные процессы формально задают компоненты приведенной полиномиальной модели.

В результате анализа прикладных задач, для которых характерно присутствие двух противоположных процессов можно заключить, что в полиномиальной модели искомый параметр встречается дважды, формируя две независимые компоненты: в первой степень при искомом параметре плюс единица, во второй в степени минус единица. Таким образом, описанные системы могут быть описаны следующей моделью:

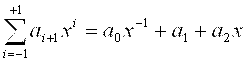                                               2

где    – переменная;

 – коэффициент, пропорциональный скорости изменения второго (обратного) процесса системы с изменением переменной;

 – свободный член модели;

 – коэффициент, пропорциональный скорости изменения первого (прямого) процесса системы с изменением переменной .

Графически прямой и обратный процессы проиллюстрированы на рисунке ниже, где функции  и  задают соответственно первую и вторую компоненты модели, а результат их сложения  описывает функционирование системы в целом (при некоторых фиксированных значениях коэффициентов).

Из графика видно, что основным свойством полиномиальных моделей, степени переменных которых по модулю не превышают единицу, является их унимодальность, т. е. единственность точки оптимума. В ходе исследования было доказано существование точки глобального экстремума и получено аналитическое решение модели (2) [4]. В частном случае, при :

.

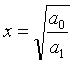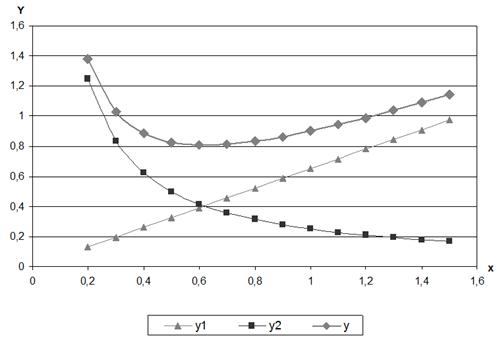
Рисунок 1 – Зависимость выходной величины y от неизвестной x для прямого и обратного процессов и их совместного действия

Таким образом, существуют все предпосылки для применения предложенной полиномиальной модели, степень переменных которой по модулю не превышает единицу при исследовании проблемных ситуаций, возникающих в качественно различных предметных областях.

Список литературы:

1.Гиг Дж. ван Прикладная общая теория систем: Пер. с англ. – М.: Мир, 1981. – 336 с., ил.

2.Гроппен В.О., Мирошников А.С. Модели управления системой оптимальной параллельной обработки информации в ЛВС СКГТУ // Труды Северо-Кавказского государственного технологического университета. Выпуск 7. – Владикавказ, 2000.

3.Петров А.Ю. Многофакторная оптимизация задачи антивирусной защиты. // Вестник Воронежского государственного технического университета. 2011. № 7. С. 137—144.

4.Петров А.Ю. Эффективные стратегии защиты ЭВМ от вирусных атак // Информатизация образования и науки. 2010. № 4(8). С. 66—76.