Статья опубликована в рамках: II Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 08 мая 2012 г.)
Наука: Информационные технологии
Секция: Математическое моделирование, численные методы и комплексы программ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ УСТАНОВИВШЕГОСЯ НЕЛИНЕЙНО ТЕРМО-НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ТЕПЛОИЗОЛИРОВАННОГО СТЕРЖНЯ ОГРАНИЧЕННОЙ ДЛИНЫ ПРИ ВОЗДЕЙСТВИИ ТЕПЛОВОГО ПОТОКА И ТЕПЛООБМЕНА
Жумадиллаева Айнур Канадиловна
канд. техн. наук, ЕНУ им. Л. Гумилева, г. Астана
Кудайкулов Анарбай Кудайкулович
д-р физ.-мат. наук, профессор ЕНУ им. Л. Гумилева, г. Астана
Ташенова Жулдыз Мусагуловна
ст.преподаватель ЕНУ им. Л. Гумилева, г. Астана
Нурлыбаева Эльмира
докторант, КазНТУ им. К. Сатпаева, г. Алматы
Е-mail:ay8222@mail.ru
В качестве несущего элемента конструкций рассмотрим горизонтальный стержень ограниченной длины ![]() площадь поперечного сечения
площадь поперечного сечения ![]() , которого постоянна по длине стержня. Оба конца стержня считаем защемленными. Боковая поверхность стержня по всей длине теплоизолирована. На площадь поперечного сечения левого конца стержня подведен тепловой поток, мощностью
, которого постоянна по длине стержня. Оба конца стержня считаем защемленными. Боковая поверхность стержня по всей длине теплоизолирована. На площадь поперечного сечения левого конца стержня подведен тепловой поток, мощностью ![]() . Через площадь поперечного сечения правого конца происходит теплообмен с окружающей его средой. При этом коэффициент теплообмена
. Через площадь поперечного сечения правого конца происходит теплообмен с окружающей его средой. При этом коэффициент теплообмена ![]() , а температура окружающей среды
, а температура окружающей среды ![]() . Требуется разработать математическую модель установившегося термо-напряженно-деформированного состояния исследуемого стержня. Расчетная схема задачи приводится на рисунке – 1.
. Требуется разработать математическую модель установившегося термо-напряженно-деформированного состояния исследуемого стержня. Расчетная схема задачи приводится на рисунке – 1.
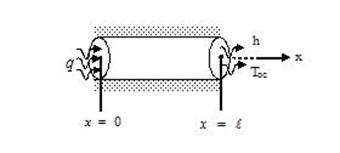
Рисунок 1. Расчетная схема рассматриваемой задачи
Коэффициент теплопроводности и теплового расширения материала стержня обозначим соответственно через ![]() и
и ![]() . Модуль упругости материала будет
. Модуль упругости материала будет ![]() . Здесь следует отметить, что
. Здесь следует отметить, что ![]() и
и ![]() . Также, при подведении теплового потока q на площадь поперечного сечения левого конца стержня, его значение берется с отрицательными законом. Сначала надо моделировать установившееся поле распределения температуры по длине исследуемого стержня. Для этого введем следующие обозначения
. Также, при подведении теплового потока q на площадь поперечного сечения левого конца стержня, его значение берется с отрицательными законом. Сначала надо моделировать установившееся поле распределения температуры по длине исследуемого стержня. Для этого введем следующие обозначения
![]()
![]()
![]() (1)
(1)
Далее с учетом физической сущности исследуемой задачи поле распределения температуры по длине исследуемого стержня аппроксимируем полным полиномом второго порядка
![]() (2)
(2)
где ![]()
![]()
![]() (3)
(3)
При этом 

 (4)
(4)
Тогда градиент температуры в пределах длины стержня имеет следующий вид
![]()
![]() (5)
(5)
Здесь следует отметить, что поле распределение температуры и его градиент температуры должны удовлетворять закону сохранения энергии. Функционал полной тепловой энергии для рассматриваемого стержня имеет следующий вид [2, с. 194]

![]() (6)
(6)
где ![]() - площадь поперечных сечений концов стержня.
- площадь поперечных сечений концов стержня.
Теперь каждый интеграл в выражении функционала рассмотрим отдельно
![]() ; (7)
; (7)
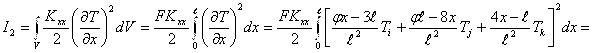
![]() ; (8)
; (8)
![]() ; (9)
; (9)
Далее подставляя (7—9) в (6) находим интегрированный вид функционала I.
![]() ; (10)
; (10)
Теперь минимизируя этот функционал получим основную разрешающую систему линейных алгебраических уравнений
 (11)
(11)
В этой системе сумма коэффициентов температур будет равна нулю
 (12)
(12)
Эти равенства являются признаками выполнения закона сохранения энергии.
Решая систему (11) определим значения температур в фиксированных сечениях
 (13)
(13)
Подставляя эти значения в (2) находим закон распределения температуры по длине исследуемого стержня
 (14)
(14)
где ![]()
Из (14) видно, что закон распределения в рассматриваемом стержне будет иметь линейный характер.
В целях исследования сходимости и точности полученного решения рассматриваемый стержень дискретизировали 2, 4, 6, … 100 квадратичными элементами. При этом число уравнений соответственно было 5,9,13, … 201, но во всех случаях дискретизации получили один и тот же закон распределения температуры по длине рассматриваемого стержня. Предположим, что левый конец рассматриваемого стержня жестко защемлен. Тогда этот стержень из-за теплового расширения будет удлиняться. Это удлинение можно определить по [1, с. 35—39]
 (15)
(15)
Кроме того, проведеные серии экспериментов [3] показал, что коэффициент теплового расширения материала стержня зависит от температуры. С учетом закона распределения температуры зависимость представим в виде следующего полного полинома второго порядка
![]()
![]() (16)
(16)
здесь ![]() известные постоянные. Тогда подставляя (14) и (16) в (15) имеем, что
известные постоянные. Тогда подставляя (14) и (16) в (15) имеем, что

![]() (17)
(17)
Если принять, что ![]() , то в этом случае будет
, то в этом случае будет
![]() (17/)
(17/)
Теперь предположим, что оба конца рассматриваемого стержня жестко защемлены. В этом случае этот стержень не может удлиняться. Но за счет процесса теплового расширения в стержне возникает сжимающее усилие, а также упругие, температурные и термоупругие составляющие деформаций и напряжений. Наряду с этим формируется поле перемещений. Для определения законов распределения этих параметров необходимо сформулировать потенциальную энергию упругих деформаций стержня с учетом поля температур [2, c. 124]
![]() (18)
(18)
где V - объем исследуемого стержня; ![]() поле распределения перемещений;
поле распределения перемещений; ![]() упругая составляющая деформаций;
упругая составляющая деформаций; ![]() упругая составляющая напряжения;
упругая составляющая напряжения;
Здесь наподобие поля температур, поле перемещения также представим в виде
![]()
![]() (19)
(19)
где ![]()
![]()
![]() (20)
(20)
Тогда градиент перемещение имеет следующий вид
![]()
![]() (21)
(21)
Кроме того, серии эксперимента показывают что модуль упругости материала стержня зависит от температуры [3, с.228]. В связи с этим, поле распределения значение модуля упругости по длине стержня аппроксимируем полным полиномом второго порядка
![]()
![]() (22)
(22)
здесь ![]() известные постоянные. Теперь пользуясь соотношениями (21-22) вычислим интеграл первого члена в выражении функционала потенциальной энергии
известные постоянные. Теперь пользуясь соотношениями (21-22) вычислим интеграл первого члена в выражении функционала потенциальной энергии

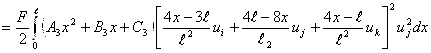
здесь необходимо учесть что, из-за защемления обеих концов стержня имеет место
![]()
тогда выражение ![]() имеет следующий вид
имеет следующий вид
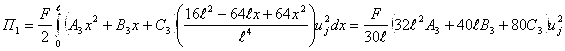 (23)
(23)
аналогично, пользуясь (14), (16) и (22) вычислим интеграл второго члена функционала потенциальной энергии
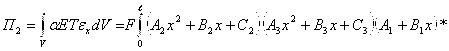
*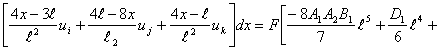
![]()
где  (25)
(25)
теперь подставляя (23-24) в (18) находим интегрированный вид функционала ![]()
![]() (26)
(26)
где 
далее минимизируя ![]() по
по ![]() находим разрешающие уравнение
находим разрешающие уравнение
![]() (28)
(28)
отсюда определим ![]()
![]() (29)
(29)
подставляя найденное значение ![]() в выражение (19), и учитывая, что в нашем случае
в выражение (19), и учитывая, что в нашем случае ![]() , определим поле перемещения
, определим поле перемещения

![]() (30)
(30)
Тогда поле упругой составляющей деформации из (30) определяется следующим образом
![]() (31)
(31)
Соответствующая составляющая напряжения определяется по закону Гука
![]() (32)
(32)
Температурные составляющие деформации определяются следующим образом
![]()
![]() (33)
(33)
![]()
![]() (34)
(34)
Тогда термо-упругие составляющие деформации и напряжения определяется по формуле
![]()
![]() (35)
(35)
Величина возникающего сжимающего усилия R определяется на основе обобщенного закона Гука, т. е.
![]() (36)
(36)
Таким образом выясним, что используя закон сохранения энергии в сочетании применения аппроксимационных сплайн функций, можно построить математическую модель установившегося термо-напряженно-деформированного состояния защемленного двумя концами стержня ограниченной длины находящегося под одновременным воздействием теплоизоляции, теплового потока и теплообмена. При этом построенная модель для рассмотренной задачи позволяет получить точное решение для рассмотренной задачи.
Список литературы:
1. Ноздрев В. Ф. Курс термодинамики: учеб. пособие. М.: Мир, 1967. – 247 с.
2. Седов Л. И. Механика сплошной среды. Т. 1:монография. М.: Москва, 1970. – 492 c.
3. Химушин Ф. Ф. Жаропрочные стали и сплавы: учеб. пособие. М.: Металлургия, 1969. – 749 с.
дипломов

Оставить комментарий