ИСТОРИЯ АЛГОРИТМИЧЕСКОЙ МУЗЫКАЛЬНОЙ КОМПОЗИЦИИ

Славщик Арсений Алексеевич

аспирант, Сибирский Федеральный Университет, Институт Космических и Информационных Технологий, НУЛ САПР

Е-mail: arssanderson@yandex.ru

1. Античность

Алгоритмической музыкой (алгоритмической музыкальной композицией) называют процесс создания музыкальных отрывков, последовательностей и композиций с помощью математических моделей, правил и алгоритмов.

Музыка и математика постоянно переплетались, начиная с незапамятных времен. В античности музыка считалась ответвлением математики. Аврелий Кассиодор описывал математику как союз четырех дисциплин: арифметики, музыки, геометрии, и астрономии.

Первый опыт по формализации музыкальных звуков с помощью математических методов принадлежит Пифагору. В области гармоники Пифагором были произведены важные акустические исследования, приведшие к открытию закона, согласно которому первые (то есть самые главные, самые значимые) консонансы определяются простейшими числовыми отношениями 2/1, 3/2, 4/3. Так, половина струны звучит в октаву, 2/3 — в квинту, 3/4 — в кварту с целой струной. «Самая совершенная гармония» задаётся четвёркой простых чисел 6, 8, 9, 12, где крайние числа образуют между собой октаву, числа, взятые через одно — две квинты, а края с соседями — две кварты. [5, c. 12—16].

2. Средние Века

Первый известный пример применения алгоритмического подхода к сочинению музыки принадлежит итальянскому теоретику музыки Гвидо д’Ареццо (1026), разработавшего соответствующий метод привязки текста к нотам. Каждая нота была назначена определенной гласной, таким образом, мелодия варьировалась, исходя из положения гласных в тексте. Стандартная 12-нотная октава была размечена следующим образом:

Г A B C D E F G a b c d e f g

Затем под этой строкой размещались три цикла гласных следующим образом:

Г A B C D E F G a b c d e f g

a e i o u a e i o u a e i o u

После этого композитору оставалось составить мелодию, пользуясь такой таблицей, исходя из извлеченных текстовых гласных [5, c. 17—20].

3. Классический период

Следующим примером попытки применения алгоритмических процедур в докомпьютерную эпоху являются музыкальные кости Моцарта. В данном случае использовались музыкальные фрагменты, которые должны были быть объединены исходя из бросков кости.

Рисунок 1 – Музыкальные кости Моцарта для 16-тактного менуэта

Номера сверху обозначают восьмые части вальса, а номера слева – возможные комбинации двух брошенных кубиков. Числа внутри матрицы соответствуют количеству тактов музыкальных фрагментов, которые затем объединяются для создания алгоритмического вальса [6, c. 2—3].

Еще одна математическая модель, использовавшаяся в искусстве на протяжении веков – золотое сечение. Под золотым сечением (обозначающимся греческой буквой ) подразумевается точка, делящая любой сегмент на такие две части, что соотношение размера более большой части по отношению к маленькой равно соотношению всего сегмента по отношению к большей части.

Золотое сечение неразрывно связано с последовательностью чисел Фибоначчи, открытую Леонардо Пизанским в 13 веке:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….,

где каждое последующее число является суммой двух предыдущих.

Данная последовательность всегда привлекала различных композиторов, использующих ее в качестве структурной схемы. По отношению ко всей длине произведения точка золотого сечения приходится примерно на 61,8 % хронометража. Обычно композиторы оставляют на данную точку кульминацию отрывка или драматический момент. Самым ранним примером использования такого подхода можно назвать мотет английского композитора Томаса Таллиса «Положиться на кого-то другого» - в золотой середине этого произведения идет такт полной тишины, за которым следует вступление хора из 40 голосов. Также использование золотого сечения можно встретить в произведениях таких композиторов как Шуберт, Бах, Дебюсси [5, c. 23—26].

4. XX век

Бурное развитие науки и, в частности, математики, начавшееся с середины XIX века, позволило композиторам и ученым воплощать в своих трудах такие идеи, которые ранее казались невозможными. В 20—30х годах двадцатого века, украинский композитор и музыкальный теоретик Иосиф Шиллингер (1985—1943), иммигрировавший в США, развил свою «систему музыкальный композиции Шиллингера» - объемное произведение размером в две тысячи страниц. Данная система покрывала все фундаментальные аспекты музыкальной композиции – контрапункты, ритмы, гармонии и т. д.

Основной принцип работы этой системы заключался в использовании результирующего вектора (система была по сути геометрической) взаимовлияющих периодических колебаний на квадратную область ритмических и структурных пропорций, с последующей проекцией на области нот и аккордов, контрапунктов, гармонических прогрессий, эмоциональных и семантических аспектов.

Данная работа была встречена резкой критикой за псевдонаучность, отсутствие внятных математических обоснований, и слишком сложный, непостоянный и сбивчивый стиль изложения. Однако именно эта работа определила направления многих будущих научных исследований в области алгоритмического сочинения музыки, и вернула интерес к сфере, забытой на несколько веков [4, c. 125—131].

Первым же человеком, использовавшим математический подход в музыке не в качестве инструмента, а в качестве принципа ее сочинения, был греческий архитектор и музыкант Яннис Ксенакис (1922—2001). По его словам, «с появлением электронных компьютеров композитор станет чем-то вроде пилота: ему останется нажимать кнопки, вводя координаты, и осуществлять контроль над путешествием корабля в пространстве музыки» [12].

В 50-х последним словом авангардистской мысли был так называемый «сериализм» - сложнейшим образом устроенная музыка, которая воспринималась как акустический пуантилизм - то есть состояла из отдельных звуков, висящих в пустоте. На слух никакой логической связи между этими разнородными звуками обнаружить было невозможно, всё вместе производило впечатление бессистемного, визгливого и довольно разреженного акустического пара. Ксенакис написал статью против сериалистического метода, считая, что параметры отдельных звуков не имеют значения, и, разумеется, восстановил против себя весь европейский авангард.

Ксенакис прменил к алгоритмическому сочинению музыки стохастические формулы. Более подробно это можно описать на примере его композиции «Брошенное эхо» для 21 инструмента. Данная композиция была написана путем создания сетки из 28 колонок и 7 строк. Каждая строка представляла собой группу инструментов, а каждая колонка – временной период. Ксенакис создавал определенное число музыкальных событий и случайным образом назначал их каждой ячейке. Внутри каждой ячейки он выбирал высоту звука и время смены одного события другим. В частности, он генерировал число событий с помощью распределения Пуассона, время смены отрезков с помощью экспоненциального распределения, высоту тона путем применения равномерного распределения. Скорость Глиссандо же определялась распределением Максвелла-Больцманна [13, c. 79—110].

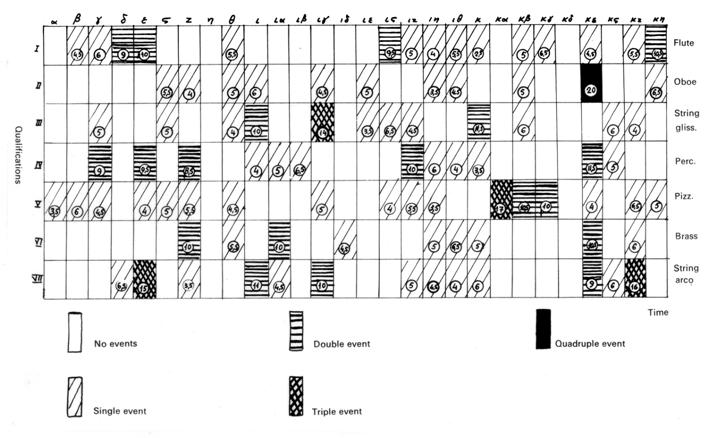
Рисунок 3 – сетка Ксенакиса, описанная в его книге «Формализованная музыка»

Лежарен Хиллер (1924—1994) – американский композитор и доктор химических наук, и, позднее, магистр музыки, первым применил компьютер для алгоритмического сочинения музыки. Его самое знаменитое детище «Сюита Иллиака для струнного квартета» (Илииак – название компьютера, на котором она была разработана) – первая композиция, «сочиненная» машиной (1955).

Данная сюита состояла из четырех частей. Первая часть была основана на серии нот, сгенерированных случайно, и, попарно объединенных в соответствии с правилами полифонии XVI века, описанными Джованни Палестриной (итальянский композитор-полифонист). Данные правила содержали три составляющие: мелодическую (ноты, включенные в октаву; ноты, повторение которых запрещено), гармонические (были разрешены только такие интервалы – унисон, октава, минорные или мажорные квинты, сексты, терции; увеличенные кварты считались диссонансными), и правила смешивания (запрет на параллелизацию квинт и октав и т. д.). Вторая часть основывалась практически на тех же принципах, только заданными в соответствии со строгими арифметическими операциями. В третьей части были добавлены правила, описывающие ритм и темп. В четвертой же части компьютеру было доверено выбирать подходящие ноты, руководствуясь вероятностными методами Марковских цепей. Случайный процесс был основан на убеждении, что в последовательности событий, выбор нового события (в данном случае, ноты), тесно связан с непосредственно предшествующем событием [8].

«Сюита Илииака» стала первым примером применения системы, основанной на знаниях в сфере алгоритмического сочинения музыки. Это был первый опыт композиции, удовлетворительно звучащей для человеческого восприятия (особенно ее вторая часть). Данное произведение пользовалось большой популярностью и неоднократно переиздавалось на аудионосителях.

Первым и единственным ученым, занимавшимся проблемой алгоритмического сочинения музыки в нашей стране был советский музыкант и математик Рудольф Зарипов. В 1960 году на ЭВМ УРАЛ он смоделировал одноголосые марши и вальсы [1, c. 17—19].

В программе этой ЭВМ каждая нота была обозначена пятизначным числом, в котором первые две цифры обозначали порядковый номер звука, третья цифра – длительность звука, четвертая и пятая – высоту звука. Машина должна была заканчивать мелодию всегда первой ступенью лада, и приближаться к концу наиболее короткими интервалами. Были запрещены последовательности из шести нот подряд в одном направлении и парные шаги, превышающие в сумме октаву. Моделирование мелодии производилось с помощью случайного процесса, ограниченного данными правилами.

Эксперимент дал удовлетворительный результат: некоторые мелодии были неприемлемы даже по меркам музыкального авангарда того времени.

5. Современные подходы

Самыми используемыми в последние несколько десятилетий подходами к решению задачи алгоритмической композиции можно назвать несколько техник – Л-системы (системы, основанные на знаниях), клеточные автоматы, генетические алгоритмы, нейронные сети (обучающиеся системы).

Теория хаоса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному, как хаос. К частным случаям теории хаоса можно отнести знаменитый Эффект бабочки, а к повлиявшим на развитие алгоритмического сочинения музыки - теорию Фракталов и Л-системы [2, c. 44].

Л-системы были созданы в 1968 году венгерским ботаником Аристидом Линденмайером для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов. Впервые для решения задач автоматической генерации музыки их применил в своей диссертации 1996 года американский программист и композитор Люк Дюбуа. Работа Л-системы начинается с определения трех наборов параметров – алфавита (список символов, которыми будет оперировать система, как на входе, так и на выходе, в нашем случае, например, ноты), набора правил (например, классических законов гармонии) и аксиомы (символ или строка символов для начального ввода) [11, c. 91—99].

Л-системы относятся к экспертным системам, основанным на знаниях и заданных наборов правил. К таким системам также можно отнести уже упоминавшиеся Марковские цепи, в которых вероятность перехода от одной ноты к другой вычисляется на основании матрицы вероятностных переходов, исходя из заранее определенных статистических правил [10, c. 17—19].

Другой современный подход – использование Клеточных автоматов, изобретенных американским математиком Джоном фон Нейманом в 1966 году. Клеточный автомат может мыслиться как стилизованный мир. Пространство представлено равномерной сеткой, каждая ячейка которой, или клетка, содержит несколько битов данных; время идет вперед дискретными шагами, а законы мира выражаются единственным набором правил, скажем, небольшой справочной таблицей, по которой любая клетка на каждом шаге вычисляет свое новое состояние по состояниям ее близких соседей. Таким образом, законы системы являются локальными и повсюду одинаковыми.

Первым клеточные автоматы в алгоритмической музыке применил бразильский композитор, получивший степень доктора математических наук в Великобритании, Эдуардо Рек Миранда, создав интерактивную систему CAMUS [7]. CAMUS генерировала мелодию на основе двух клеточных автоматов: игра в «жизнь» Джона Неймана, и Demon Cyclic Space Больцмана. Игра в «жизнь», изобретенная Джоном Конвеем и популяризованная Мартином Гарднером, использует следующие правила: если клетка имеет двух "живых" соседей, она остаётся в прежнем состоянии. Если клетка имеет трёх "живых" соседей, она переходит в "живое" состояние. В остальных случаях клетка "умирает". Несмотря на свою простоту, система проявляет огромное разнообразие поведения, колеблясь между очевидным хаосом и порядком.

Первый клеточный автомат отвечает за выбор нот. Каждая клетка соответствует триаде: первая нота дана заранее определенной из последовательности из 12 нот, а две другие - определены координатами клетки в музыкальном пространстве. Demon Cyclic Space же отвечает за оркестровку, он определяет, какой из инструментов будет подыгрывать основной мелодии.

Генети́ческий алгори́тм — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию.

Первопроходцем в применении генетических алгоритмов в алгоритмический музыке считается Джон Бильс – профессор Рочестерского института технологий (Нью-Йорк, США), применивший его для генерации джазовой соло-импровизации в своей программе GenJam [3].

Работа генетического алгоритма начинается с применения эквивалента биологического образования новых генов на пространство случайно распределенных решений для нахождения в итоге оптимального набора [9, c. 3—6]. Решения представлены хромосомами, а строки аллель – строками чисел, и задача рекомбинации генов сводится к созданию новых аллелей из аллель, взятых от родительских хромосом путем применения генетических операторов, в большинстве случаев, мутации и скрещивания. Перебирание хромосом продолжается до достижения определенного условия прерывания. Генетические алгоритмы в задаче автоматического музицирования разделяются по виду использованной фитнесс-функции – степень приспособленности хромомом может быть оценена исходя из заранее заданных четких условий, либо может быть определена непосредственно человеком при прослушивании и субъективной оценке.

Под обучающимися системами понимают системы, в которых не задано априорных правил, а система сама обучается чертам на примерах. Чаще всего, под такими системами подразумеваются искусственные нейронные сети, имитирующие работу нейронов мозга человека и способные обучаться на основе предоставленных примеров. Обычно такие системы используются в другой отрасли музыкальной математики: при распознавании музыкальных отрывков, например для решения задач реставрации потерянных музыкальных данных или для составления автоматических партитур. Поэтому данный метод не сильно развит в алгоритмической музыке. Существует несколько систем, использующих нейронные сети, например, HARMONET или CONCERT. HARMONET используется для оркестровки мелодий на основе обучении правилам гармонии И. Баха. Первым человеком, применившим нейронные сети к решению задач алгоритмической композиции, был Питер Тодд, профессор психологии и информатики из Калифорнии.

Также, одно из самых последних направлений в сфере алгоритмической композиции – моделирование эмоциональной нагрузки произведений для устранения проблемы сухого математического расчета и привнесения в машинную музыку элементов настроений и смысла, вкладываемых человеком в сочиняемые композиции.

Список литературы:

1.Пучков C. В. Музыкально-исторические предпосылки развития становления электронной (технической) музыки // С. В. Пучков, М. Г. Светлов. Музыкальные компьютерные технологии – СПб., 2005 – Гл.1. – С. 17—19.

2.Aschauer Daniel – Algoritmic Composition – Master Thesis, Austria, 2008 – 44 c.

3.Biles John – Autonomous GenJam / J. Biles // GECCO 2001

4.Degazio Bruno – The Schillinger System of Musical Composition and Contemporary Computer Music, Diffusion, 1988 – 125-131 c.

5.Dias-Geres Gustavo – Algorithmic composition: using mathematical models in music composition: Doctor of musical arts [Manhattan school of music] – 2000 – 12—20, 23—26 c.

6.Edwards Michael – Computational thinking in music / M. Edwards // University of Edinburgh, Computational Thinking Seminar, 2009 – 2—3 c.

7.Miranda Eduardo Reck – CAMUS Tutorial [электронный ресурс] – 2001 – Режим доступа: http://tamw.atari-users.net/camus/camustut.htm

8.Nunzio Alex – Illiac suite [электронный ресурс] – 2011 – Режим доступа: http://www.musicainformatica.it/english/topics/illiac_suite.php

9.Papadopoulos George – AI Methods for Algorithmic Composition : A survey, a Critical View and Future Prospects / P. George //AISB Symposium on Musical Creativity, 1999 – 3—6 c.

10.Peck Jacob M. - Explorations in Algorithmic Composition: Systems of Composition and Examination of Several Original Works – Bachelor’s of Science Degree in Computer Science – State University of New York, 2011 – 17—19 c.

11.Pestana Pedro – Lyndenmayerr systems and theory of fractals / P. Pestana // Chaotic Modeling and Simulation, 1, 2012 – 91—99 c.

12.Xenakis Yannis [Электронный ресурс]: А. Горохов – 2001. – Режим доступа: http://www.muzprosvet.ru/xenakis.html - Загл. с экрана.

13.Xenakis Yannis– formalized music – thought and mathematics in composition / Y. Xenakis – harmonologia series 6, Pentragon press – 1992 – 79—110 c.