Анализ корректности использования статистических методов при исследовании связей между признаками

Мазорчук Мария Сергеевна

канд. техн. наук, доцент, Национальный аэрокосмический университет «ХАИ», г. Харьков

Сухобрус Анатолий Андреевич

канд. техн. наук, профессор Национальный аэрокосмический университет «ХАИ», г. Харьков

Добряк Виктория Сергеевна

аспирант, Национальный аэрокосмический университет «ХАИ», г. Харьков

E-mail:

При исследовании связей между признаками в социальной сфере, экономике, образовании часто возникают проблемы с выбором адекватных статистических методов для построения качественных моделей, отображающих зависимость между явлениями и процессами. В технических науках использование методов математической статистики является достаточно понятным, поскольку большинство исследуемых параметров измеряются в метрических шкалах, что дает возможность исследователю использовать параметрические методы оценки [1]. В социологии, педагогике, психологии, экономике часто приходится иметь дело с качественными данными, которые могут измеряться в номинальных либо порядковых шкалах [4]. В этом случае прибегают к непараметрическим методам оценки. Однако, часто используют методы регрессионного и корреляционного анализа для порядковых и даже номинальных признаков, забывая об ограничениях и допущениях этих методов, что приводит к некачественному анализу и построению неадекватных моделей. Таким образом, актуальной является задача выбора методов, позволяющих построить качественные модели, отражающие зависимости между разнородными данными.

Целью данной работы является исследование возможных ошибок, которые могут возникнуть в ходе обработки и анализа данных и выбор адекватных методов для построения качественных статистических моделей.

Рассмотрим на примере обработки результатов тестов вступительных экзаменов возможные ошибки анализа данных. В настоящее время большое внимание в сфере образования уделяется оценки качеству тестов [3]. Например, одной из проблем является оценка качества тестов Единого Государственного Экзамена (ЕГЭ) в России и Внешнего Независимого Оценивания (ВНО) в Украине [2, 4]. Для проверки справедливости тестов строят регрессионные модели, отображающие зависимость успеваемости студентов от ряда параметров, таких как балл аттестата, средний балл по сертификатам, уровень интеллекта. В ходе оценки могут возникнуть ряд трудностей, которые не позволяют получить качественные модели, отражающие зависимость между данными признаками. Проанализируем возможные проблемы.

1.  Проблема шкал оценивания.

В средних школах Украины используется 12-ти бальная система оценивания. Результаты ВНО измеряются в шкале от 100 до 200 баллов. Оценивание в вузах осуществляется по-разному: в 4-х бальной шкале (оценки «2», «3», «4» и «5»); в 12-ти бальной; в 100-бальной. При таком разнообразии шкал расчет коэффициента корреляции Пирсона без преобразования данных просто является некорректным. Следует также учесть, что при оценивании результатов сессии и результатов ВНО используются в принципе разные шкалы оценки. Результаты сессии оцениваются «сырыми» баллами, которые вполне пригодны для оценивания учеб­ных достижений отдельных обучаемых в ходе учебных занятий. Однако они не подходят для массового тестирова­ния при проведении выпускных или вступительных экза­менов, поскольку не позволяют выявить истинных различий в уровне подготовленности экзаменуемых, сравнить их результаты между собой, правильно интерпретировать оценки. Этот факт является и причиной некорректного использования коэффициента корреляции для анализа связи между результатами теста ВНО и сессии.

Для корректного перевода оценок следует использовать методы шкалирования результатов. Наиболее известные методы преобразования первичных баллов – это метод процентильного ранга; эквипроцентильный метод; линейная Z-оценка; оценки, которые являются линейным преобразованием z-оценки (Т-шкала, оценки стандартного IQ и т. д.); шкалы станайнов и стенов [3].

2.  Проблема пропущенных и некорректных значений.

Поскольку базы данных социологических исследований, результатов тестирования являются достаточно большими (могут содержать сотни тысяч записей), то при вводе данных (даже автоматическом) и при первичной обработке могут иметь место пропущенные значения и некорректно введенные данные. Например, на рис. 1 представлены результаты ВНО и сдачи зимней сессии студентами. Как видно, из гистограммы частот, среди баллов ВНО имеют место баллы, меньшие 100, и даже отрицательные значения, и довольно много значений равных нулю отображается на гистограмме среднего балла сессии.

Такие значения часто приводят к искажению результатов. Поэтому следует предварительно исследовать данные на обнаружение ошибок, проверить закон распределения и только после этого переходить к выбору методов оценки. В данном случае, целесообразно выборку разбить на группы, и пропущенные и искаженные значения проанализировать отдельно от всей выборки.

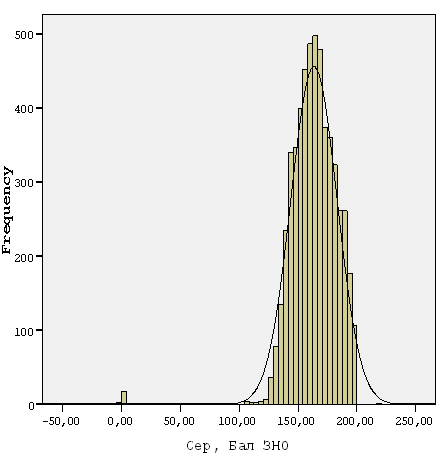
Рис. 1 Гистограммы распределения частот по результатам тестов ВНО и успеваемости в сессию

 Также возможна замена пропущенных значений на средние либо модальные значения с целью обеспечения однородности данных.

3.  Проблемы ограничений и допущений, накладываемых моделями.

Регрессионный анализ является одним из самых распространенных методов обработки результатов наблюдений. Однако этот метод базируется на ряде ограничений и допущений, нарушение которых приводит к некорректности его использования и ошибочной интерпретации результатов.

Проверка предпосылок и допущений данного метода предполагает решение комплекса задач, к которым относятся: оценка случайности зависимого признака; оценка стационарности и эргодичности исследуемых признаков; проверка гипотезы на нормальность распределения ошибок; обнаружение выбросов; оценка автокорреляции остатков; проверка постоянства математического ожидания и дисперсии ошибок; выявление мультиколлинеарности.

Оценить случайность зависимого признака можно несколькими методами, например, с использованием критерия серий либо методом последовательных разностей [6, с. 197]. Проверка стационарности (под стационарностью понимают неизменность статистических характеристик за время исследования процесса) и эргодичности (для эргодических процессов и математическое ожидание, и дисперсия, и автокорреляционная функция, вычисленные по одной реализации, будут такими же и для любой другой реализации) можно проводить с использованием критериев Стьюдента, Фишера или  Пирсона при известном выборочном распределении. При неопределенности относительно распределения исследуемого процесса используют критерии серии или тренда [6, с. 201].

Большинство выводов регрессионного анализа основаны на допущении о нормальном распределении ошибок. Это требует подтверждения с помощью критериев согласия Колмагорова-Смирнова, Пирсона или Шапиро-Уилкса, которые основаны на расчете статистик, являющихся мерами рассогласования эмпирического и теоретического распределения [1, 6].

Остальные задачи относятся к задачам проверки качества полученной регрессионной модели. Одним из важных критериев является коэффициент детерминации, который рассчитывается как отношение факторной дисперсии к общей. Коэффициент детерминации показывает, сколько процентов случаев изменения признака  приводит к изменению признака .

При анализе автокорреляции остатков регрессионной модели часто применяют критерий Дарбина-Уотсона ,

где  - остаток для -го наблюдения;  - правая последовательная разность. В общем случае автокорреляция остатков отсутствует, если 1.5<DW<2.5 [6].

Проверка постоянства математического ожидания и дисперсии регрессионных ошибок часто осуществляется на основе графического анализа ошибок. При постоянном математическом ожидании и дисперсии график регрессионных ошибок будет иметь вид, как на рис. 2 (а). На данном рисунке отображены результаты первой сессии студентов ряда вузов Украины.

Остатки должны быть нормально распределены, т.е. на графике они должны представлять приблизительно горизонтальную полосу одинаковой ширины на всем ее протяжении. Коэффициент корреляции между регрессионными остатками и переменными должен равняться нулю. График на рис. 2 (б) свидетельствуют о наличии зависимости среднего от ошибки фактора (результаты ВНО по Украине в 2011 году).

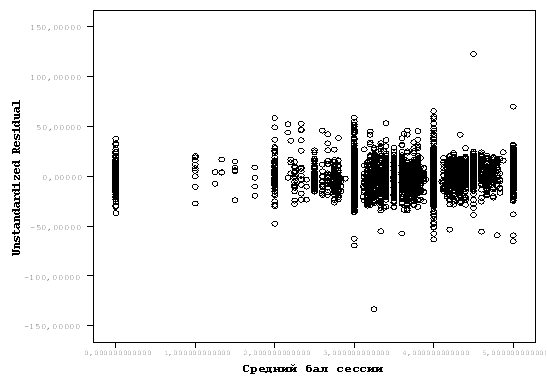 а)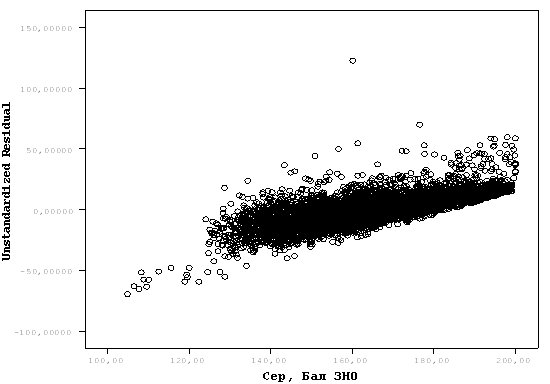

                                                                                                              б)

Рис. 2 Графический метод проверки гипотез постоянства

математического ожидания

Также, важной характеристикой, отражающей качество модели, является мультиколлинеарность факторных признаков. Высокая корреляции между входными переменными модели множественной линейной регрессии вызывает неустойчивость работы модели, когда коэффициенты регрессии сильно меняются даже при незначительном изменении исходных данных.

Таким образом, для решения задач оценки связи между признаками, которые измеряются не в метрических шкалах, а в порядковых или номинальных, целесообразно применять такие методы оценки, как бинарный, мультиноминальный и ранговый регрессионный анализы [6, с. 295]. Для выявления зависимостей хорошие результаты дают методы дисперсионного и дискриминантного анализа. Например, наряду с информацией о группирующих признаках по результатам дискриминантного анализа можно также составить уравнение дискриминантной функции, которое отображает зависимости признаков по оцениваемым группам [6, с. 374].

Список литературы:

1.Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2004. 479 с.

2.Молибоженко В. В. Математические оценки качества педагогических тестов // ПЕДСОВЕТ.ORG [Электронный ресурс] URL: http://pedsovet.org/component/option,com_mtree/task,viewlink/link_id,4409/Itemid,118/ (дата обращения: 27.04.2012).

3.Нейман Ю. М., Хлебников В. А. Введение в теорию моделирования и параметризации педагогических тестов. М.: Прометей, 2000. 168 с.

4.Пономаренко В. С. Чи можна оцінити здатність особистості до навчання? // Вісник ТІМО № 4/2011. С. 39—41.

5.Толстова Ю. Н. Логика математического анализа социологических данных, М.: Наука, 1991. 110 с.

6.Шамша Б. В., Гуржій А. М., Дудар З. В., Левикін В. М. Математичне забезпечення інформаційно-управляючих систем. Харків: Компанія «Сміт», 2005. 448 с.