Параметрические преобразования и Р-представления дескриптивных алгебр изображений

Исхаков Алмаз Раилевич

преподаватель ФГБОУ ВПО Башкирский государственный педагогический университет им. М. Акмуллы, г. Уфа

E-mail: intellab@mail.ru

Мигранов Наиль Галиханович

д-р физ.-мат. наук, проф. ФГБОУ ВПО Башкирский государственный педагогический университет им. М. Акмуллы, г. Уфа

E-mail: ufangm@yahoo.co.uk

Кузнецова Елизавета Михайловна

Мухаметова Ираида Валерьевна

Галанов Вячеслав Александрович

студенты ФГБОУ ВПО Башкирский государственный педагогический университет им. М. Акмуллы, г. Уфа

E-mail:

Введение.

Автоматизация обработки, анализа, оценивания и понимания информации, представленной в виде изображений, является одной из актуальной и узловой проблемой теоретической информатики, искусственного интеллекта и теории распознавания образов. Разнообразие применяемых методов не заменяет необходимости иметь некоторую регулярную основу для систематизации и выбора адекватных методов анализа изображений, единообразного представления обрабатываемых данных (изображений), отвечающих требованиям стандартных алгоритмов распознавания к исходной информации, построения математических моделей изображений, ориентированных на задачи распознавания, и в целом - наличия некоторого универсального языка для единообразного описания изображений и преобразований над ними. В рамках указанной проблемы ведущим направлением стала «алгебраизация» обработки, анализа и распознавания изображений [3, с. 100-109], заключающаяся в разработке и исследовании различных алгебр изображений (АИ). Основной целью алгебраического подхода является построение теоретического аппарата, обеспечивающего представление изображений и преобразований над ними в виде алгебраических структур, позволяющих использовать в анализе и распознавании изображений математические методы [9, с. 518-541].

В области распознавания образов и анализа изображений выделяют следующие основные стадии «алгебраизации»: математическая морфология (Г. Матерон (Matheron), Ж. Серра (Serra) [1970-е]); алгебра алгоритмов (Ю. И. Журавлев [1970-е]); теория образов (У. Гренандер (Grenander) [1970-е]); теория категорий в области распознавания образов (М. Павел (Pavel) [1970-е]); АИ (Ж. Серра, С. Стернберг (Sternberg) [1980- е]); стандартная алгебра изображений (САИ) (Г. Риттер (Ritter) [1990-е]); дескриптивная алгебра изображений (ДАИ) (И. Гуревич [1990- е]); ДАИ1К (И. Гуревич, В. Яшина [2002 и далее]).

Разработанный к настоящему моменту времени математический аппарат ДАИ [9, c. 518-541] и ДАИ1К [8, с. 298-328] обладает рядом недостатков: неудобная терминология формальных обозначений, отсутствие конструктивности в описаниях методов и операций, обобщенное определение операции структуризации, слабая связь семантической и контекстной информации изображений и т. п. В данной статье предлагается формализованный подход к описанию параметрических преобразований и Р-представлений ДАИ.

Реализации изображений в ДАИ.

Пусть объектом наблюдения является совокупность объектов или процессов действительности, которую будем называть сценой наблюдения или просто сценой. Изображение сцены может быть задано в разных форматах, которые называются его реализациями [9, c. 518–541]. Таким образом, изображение  может быть задано в виде совокупности его реализаций , соответствующих бинарным, полутоновым и цветным (полноцветное или палитровое) изображениям:

1.  , где ;

2.  , где ;

3.  , где .

По умолчанию цветные реализации представляются в полноцветной форме.

Параметрические преобразования в ДАИ.

Параметрические преобразования, в отличие от процедурных преобразований, позволяют для заданного изображения вычислить значение заранее выделенного параметра, характеризующего содержимое исходного изображения в виде числа, числовой последовательности (вектора), матрицы, функции или аналитической зависимости и т. п.

Введем обозначения для параметрических представлений, как в случае с процедурными преобразованиями (табл. 1).

Таблица 1.

Параметрические преобразования

Согласно [3, с. 20-32], в качестве принципа классификации выберем «модальность» признаков, что обуславливает разделение множества всех возможных признаков на: детерминированные, вероятностные, логические и структурные. Из этого числа исключаются логические признаки, что обусловлено их отнесением к системам принятия решений. Для простоты вычислений, в дальнейшем будут использованы бинарные или полутоновые реализации изображений.

Определение:Параметрическим преобразованием реализации изображения  с параметром  называется отображение

, где  и   (*)

Элементы множества  являются обозначениями признаков соответственно: детерминированных, вероятностных, и структурных. Эта классификация не является универсальной, поэтому приведем дополнительные классификации, позволяющие рассмотреть разнообразие методов их вычисления с разных ракурсов:

1.  по форме существования выделяются [3, с. 15-17]: количественные и качественные;

2.  по типу значений выделяются: целые, рациональные, действительные, комплексные, символьные и сложные символьные (строчные или последовательности символов);

3.  по виду области определения выделяются [4, с. 13-18]: дискретные и непрерывные;

4.  по сложности выделяются: скалярные, векторные, матричные и тензорные;

5.  по модальности выделяются [1, с. 201-230]; [7, с. 78-85]: физические, геометрические, функциональные и топологические;

В силу однотипности в структуре методов вычисления детерминированных признаков в статье их формализация не приводится, а в качестве символьных обозначений используется  или . Детерминированные признаки представляют собой частный случай вероятностных признаков [3, с. 32-34]. Так как некоторая величина считается вероятностной, если она может принимать не одно значение, а целое множество, то в таком аспекте детерминированный признак является вероятностной величиной, только с единственным значением, вероятность появления которого равна 1.

Под измерением вероятностного признака будем подразумевать процесс определения всех возможных значений с вероятностями их принятия. Кроме них в области компьютерного зрения [2, с. 143-184] используются также «статистические величины», к которым можно отнести: начальный и центральный моменты (математическое ожидание (среднее), среднеквадратичное отклонение, коэффициенты асимметрии и эксцесса), энтропия, значения минимального и максимального элементов анализируемого поля и размах (диапазон уровней). Рассмотрим реализации , где  изображения  и формализованные представления статистических характеристик с учетом принятой в ДАИ обозначений:

·     начальные моменты k-го порядка - ,

Согласно этой формулировке получаем ее частные случаи:

1.   - начальный момент 1-го порядка;

2.   - начальный момент 2-го порядка;

3.   - начальный момент 4-го порядка;

4.   - начальный момент 4-го порядка;

·     центральные моменты

1.   - центральный момент 2-го порядка. Откуда можно вычислить среднеквадратическое отклонение ;

2.   - центральный момент 3-го порядка;

3.   - центральный момент 4-го порядка;

·     коэффициент асимметрии ;

·     коэффициент эксцесса ;

·     энтропия , где ;

·     избыточность или относительная энтропия , где  и  - максимальный и минимальный уровни поля (для бинарной реализации , для полутоновой реализации );

К логическим признакам относятся, прежде всего, признаки, не имеющие количественного выражения. Они представляют собой суждения качественного характера на наличие или отсутствие некоторых свойств или некоторых элементов у распознаваемых объектов или явлений. Также логическим можно отнести признаки, у которых важна не величина признака, а лишь факт попадания или непопадания ее в заданный интервал. В пределах этих интервалов появление различных значений признаков у распознаваемых объектов предполагается равновероятным. На практике логические признаки подобного рода имеют место в таких ситуациях, когда ошибками измерений можно пренебречь, либо интервалы значений признаков выбраны, что ошибки измерений не оказывают влияния на достоверность принимаемых решений относительно попадания измеряемой величины в заданный интервал [3, с. 10-43]. Вероятностные признаки сводятся к логическим признакам аналогично детерминированным; если бы логические признаки существовали как отдельная разновидность, то для измерения логических признаков разных типов нужно было бы разрабатывать отдельные измерители. Определение значения логического признака представляет собой простейшую систему принятия решений.

Структурные и логические признаки схожи в аспекте их формализованного представления. По сути, структурные признаки являются геометрическими объектами. Проведя аналогию между простейшими геометрическими объектами и символьными обозначениями высказываний, а также, установив взаимно однозначное соответствие логическими операциями и отношениями между геометрическими объектами, приходим к возможности записи сложного структурного объекта в форме предложения на естественном языке. Таким образом, структурный метод распознавания связан с использованием аналогии между структурой объектов и синтаксисом естественного языка. Под измерением структурного признака нужно понимать идентификацию непроизводных элементов и связей между ними [3, с. 10-43].

Методы выделения непроизводных элементов можно разделить на две группы. В первой из них делается упор на границы, а во второй – на области изображения. В настоящее время основным методом, используемым в описании границ, является цепные коды Фримена [5, с. 56-178]; [2, с. 203-213]. Но наряду с цепными кодами Фримена существуют и другие, например: 1) кодирование по трем признакам: длине текущего элементарного вектора, направлению поворота при переходе к следующему элементарному вектору и углу между соседними элементарными векторами; 2) кодирование текущего элементарного вектора трехразрядным двоичным кодом (метод Фримена); 3) P-представление контура; 4) кодирование текущего элементарного вектора двумя его проекциями на оси координат (двухмерный код); 5) полигональное представление контура; 6) представление контура радиус-векторами, приведенными из центра тяжести фигуры; 7) представление контура в виде функции комплексного переменного; 8) представление элементарного вектора контура в плоскости квадратной сетки комплексными числами.

Ниже приведена текстовая формулировка алгоритма для бинарной реализации  изображения , использующего один из восьми способов кодирования: 1) наложить на изображение  равномерную сетку; 2) в качестве элементов границы выбрать те элементы реализации , более 50 % площади которых находится в пределах рассматриваемой фигуры; 3) выбрать из числа элементов реализации  те, которые не являются внутренними (внешние элементы фигуры); 4) применить один из 8 способов кодирования последовательности выбранных на 3 шаге элементов. Результатом применения этого алгоритма будет последовательность кодов, описывающих граничные точки фигуры, изображенной на реализации .

Пусть дана бинарная реализация  изображения , т. е. , где . Следующая формализованная запись представляет математическую модель процедуры вычисления структурных признаков  для бинарной реализации :

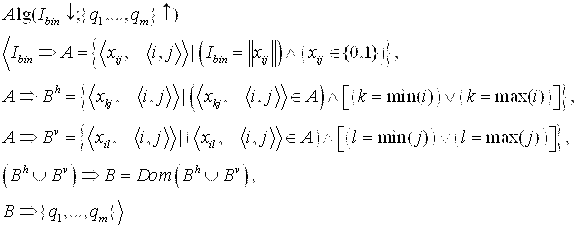
Алгоритм представляет собой параметрическое преобразование:

Другим не менее распространенным методом получения цепных кодов для границ является привлечение методов математической морфологии [2, с. 351-395] на первом шаге алгоритма. Согласно той же самой исследовательской работе граница  множества  может быть вычислена путем выполнения сначала операции эрозии  по , а затем получения разностного множества между  и результатом его эрозии:

,

где  - подходящий примитив, а роль множества  выполняет бинарная реализация . Ниже приведена математическая модель этой процедуры, которая уже является параметрической:

,

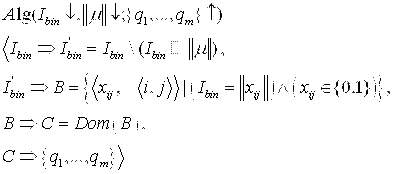где  - исходное изображение, а  - маска и параметр алгоритма.

В терминах параметрических преобразований для структурных признаков оно имеет вид:

Эту же задачу можно решать с привлечением операторов, выполняющих дискретное дифференцирование [2, с. 396-443] при использовании процедурного преобразования с операцией фильтрации, где значением параметра является вектор параметров маски фильтра :

,

где  - параметр алгоритма и параметры маски фильтра. В терминах параметрических преобразований для структурных признаков она имеет вид:

Если рассмотрим процедурные преобразования на базе операции фильтрации, то параметр  может принимать векторное значение , компоненты которого являются рангами матрицы-маски для линейных и нелинейных пространственных фильтров.

Более сложный случай описывает следующий алгоритм, когда он содержит в своей структуре два преобразования с параметрами  и . Тогда параметрическое преобразование со значением параметра  над полутоновой реализацией изображения может быть представлено следующим образом:

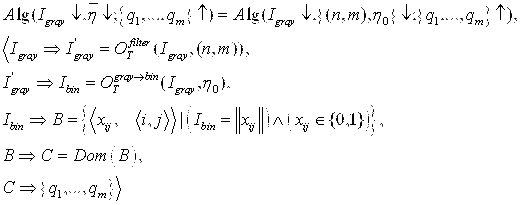
Ее общая форма будет иметь вид:

Отметим, что в данном параметрическом преобразовании использованы два процедурных преобразования: метод фильтрации полутоновой реализации  с параметрами маски , и метод пороговой конвертации полутоновой реализации  в бинарную реализацию  с параметром .

Р-представления в ДАИ.

Для формализации Р-представлений обратимся к узловой работе И. Гуревича и В. Яшиной «Описательный подход к анализу изображений: модели изображений» [9, с. 518-541].

Определение [9, с. 518-541]: Параметрическим преобразованием  над изображением  называется такая операция, применение которой к изображению  преобразовывает его в числовую характеристику , которой можно сопоставить свойства геометрических объектов, яркостных характеристик или конфигураций, образующихся за счет регулярных повторений геометрических объектов и яркостных характеристик исходного изображения.

В таком случае, придерживаясь определения Т-представления и параметрического преобразования можно сформулировать следующее определение Р-представления. Аналогичное определение приведено в работе [9, с. 518-541].

Определение [9, с. 518-541]: Р-представлением  изображения  называется формальная схема, предназначенная для получения его числовой характеристики и построенная на основании контекстной и семантической информации  с помощью параметрических преобразований  и структурирующих элементов . Множество всех корректных Р-представлений обозначается .

Определение: Реализацией Р-представления  изображения  называется применение представления  с выбранными значениями  параметров преобразований, входящих в представление к реализациям исходного изображения .

Любое корректное Р-представление из множества  можно записать следующим образом:

,

где  и .

Можно обойтись и без операции структуризации, вычислив значение искомого признака в исходном изображении. Приведем подробное математическую формулировку действий для следующей задачи: дана полутоновая реализация , нужно вычислить значение статистического момента 1-го порядка :

Приведем формализованное описание процедуры вычисления значения структурного признака в форме окружности в полутоновой реализации

Таким образом, можно записать любое отдельное действие, их комплекс или алгоритм решения поставленной задачи. Предлагаемая в данной диссертационной работе формализованная терминология является удобным инструментом для математической записи задач преобразования и анализа изображений. В следующей главе данной работы рассмотрим использование предлагаемой терминологии в ДАИ для решения поставленных задач.

Заключение

В данной статье приведены теоретические положения, полученные А. Р. Исхаковым в ходе исследований по диссертационной работе. В число основных результатов, описанных в статье, входят: виды классификаций признаков, формализация процедурных преобразований, использующих методы вычисления статистических и структурных признаков в бинарных реализациях, формализация Р-представлений для вычисления детерминированных, статистических и структурных признаков. Полученные результаты являются важными для развития алгебраического подхода к обработке, анализу и распознаванию изображений.

Список литературы:

1.Воротников С. А. Информационные устройства робототехнических систем: Учеб. пособие. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2005. – 384 с.

2.Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде Matlab. М.: Техносфера, 2006

3.Горелик А. Л. Методы распознавания: Учеб. пособие для вузов / А. Л. Горелик, В А. Скрипкин. – 4-е изд., испр. – М.: Высш. Шк., 2004. – 261 с.

4.Потапов А. С. Распознавание образов и машинное восприятие, 2007

5.Фу К. Структурные методы в распознавании образов, 1977

6.Фурман Я. А., Юрьев А. Н., Яншин В. В. Цифровые методы обработки и распознавания бинарных изображений, 1992

7.Хорн Б. К. П. Зрение роботов, 1989

8.I. B. Gurevich, V. V. Yashina. Operations of Descriptive Image Algebras with One Ring // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. Pleiades Publishing, Inc. 2006. – Vol.16,No.3.- P. 298-328.

9.I. B. Gurevich and V. V. Yashina. Descriptive Approach to Image Analysis: Image Models // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. – MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., 2008. - Vol.18, No.4. - P. 518-541.