Статья опубликована в рамках: IIIA Международной научно-практической конференции «Практические аспекты современного менеджмента» (Россия, г. Новосибирск, 05 ноября 2010 г.)
Наука: Экономика
Секция: Финансы и налоговая политика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Международной заочной научно-практической конференции «Теория и практика современного менеджмента»
Выходные данные сборника:
Выходные данные сборника: «Теория и практика современного менеджмента» (5 ноября 2010г.)
МОДЕЛИРОВАНИЕ ДИНАМИКИ ИЗМЕНЕНИЯ ДОХОДА И ИНВЕСТИЦИЙ В УСЛОВИЯХ КРИЗИСА ПО МОДЕЛИ ГУДВИНА-КАЛЕЦКОГО-НЕЙМАРКА С УЧЕТОМ ВЛИЯНИЯ ВНЕШНИХ ФАКТОРОВ
Бунин Александр Сергеевич
Главный специалист группы ипотечного кредитования
отдела розничного бизнеса,
ОАО «Нордеа Банк», г. Самара
E-mail: shilov_anton@mail.ru
Недавняя рецессия глобальной экономики, и риски возникновения второй волны этого катастрофического явления в высшей степени актуализировали проблему моделирования результатов долгосрочных инвестиций в реальный сектор экономики. Целью настоящей работы является качественный модельный анализ инвестиционной деятельности крупной компании в условиях рецессии.
Система уравнений (1), предложенная в работе [1, c. 208], предназначенная для анализа социально-экономических систем, является очень гибкой и обладает большими прогностическими и объясняющими возможностями. Величина I соответствует инвестициям из собственного дохода компании. То есть при помощи модели, описываемой системой (1) невозможно учесть влияние инвестиций, привлекаемым извне.
 , (1)
, (1)
где
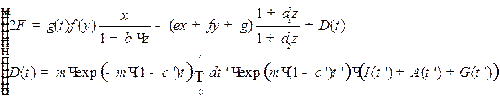 . (2)
. (2)
Чаще всего перед разработчиками крупных инвестиционных проектов стоит именно задача среднесрочного прогнозирования девелоперских проектов, таких, как инвестиции в масштабе торгового центра, длинной “галереи бутиков”, реконструкция улицы под торговую галерею и т.п. Для учета внешних инвестиций, модифицируем систему уравнений (1) следующим образом:
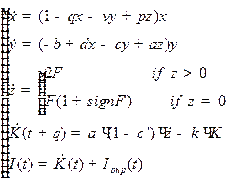 , (3)
, (3)
где внешние инвестиции 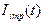 есть решение уравнения
есть решение уравнения
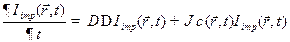 (4)
(4)
описывающего прирост объема инвестиций на отдельном центре размножения.
Рассмотрим подробнее (4). Функция 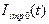 является медленно меняющейся величиной. Соответственно, удобно искать решение в виде:
является медленно меняющейся величиной. Соответственно, удобно искать решение в виде:
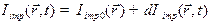 . (5)
. (5)
Выражение для 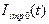 получим из условия равновесия
получим из условия равновесия
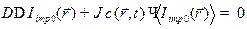 . (6)
. (6)
из которого вытекает уравнение на 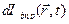 :
:
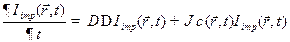 . (7)
. (7)
Рассмотрим несколько вариантов решения (7) в зависимости от размерности задачи и вида 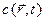 .
.
Рассмотрим одномерный случай, функция 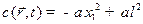 . Этот случай соответствует инвестициям в организацию уличной торговли по модели «галерея бутиков», характерной для большинства европейских и азиатских городов. Часто подобная галерея расположена в центре города в пешеходной зоне. Очевидно, что открытие нового или серьезная реконструкция уже работавшего ранее магазина оказывает серьезное влияние на «соседей». Обычно это сопровождается рекламой, что отражается на ситуации в торговом центре в целом.
. Этот случай соответствует инвестициям в организацию уличной торговли по модели «галерея бутиков», характерной для большинства европейских и азиатских городов. Часто подобная галерея расположена в центре города в пешеходной зоне. Очевидно, что открытие нового или серьезная реконструкция уже работавшего ранее магазина оказывает серьезное влияние на «соседей». Обычно это сопровождается рекламой, что отражается на ситуации в торговом центре в целом.
В двумерном случае
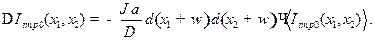 (8)
(8)
Функция Грина для двумерного оператора Лапласа имеет вид
 . (9)
. (9)
Соответственно, решение (7)
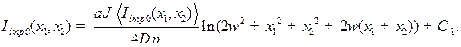 (10)
(10)
Среднее значение 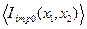 в данном случае считается численно. Решение имеет вид
в данном случае считается численно. Решение имеет вид
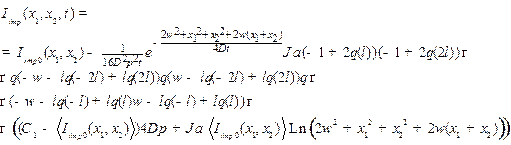 (11)
(11)
С учетом того, что величина 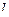 , имеющая смысл размера торгового центра, положительна и
, имеющая смысл размера торгового центра, положительна и 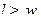 , получим
, получим
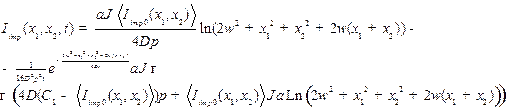 (12)
(12)
Таким образом, мы получаем направления устойчивого развития торгового центра.
В работе были проведены вычисления для двумерного случая с несколькими наборами параметров. Для оценки инвестиционного проекта было осуществлено прогнозирование поведения величин инвестиций 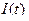 , капитала
, капитала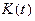 и дохода
и дохода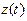 . Ниже показаны графики именно величин с несколькими наборами параметров и координат. Данные графики получены при параметрах
. Ниже показаны графики именно величин с несколькими наборами параметров и координат. Данные графики получены при параметрах  ,
,  ,
, 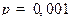 ,
, 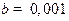 ,
,  ,
, 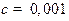 ,
,  ,
,  ,
, 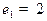 ,
,  ,
, 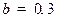 ,
, 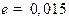 ,
, 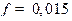 ,
,  ,
,  ,
, 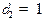 ,
, 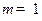 ,
, 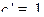 ,
, 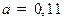 ,
, 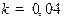 ,
,  ,
, 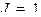 ,
, 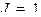 ,
,  . Также проиллюстрируем кризисные ситуации и рост в системе.
. Также проиллюстрируем кризисные ситуации и рост в системе.
Рисунки 1 и 2 соответствуют кризису. Эти графики получены при r равном 0,1, 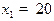 ,
, 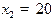 . Также приведем графики для растущей системы. Коэффициент
. Также приведем графики для растущей системы. Коэффициент 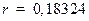 .
.
|
|
|
|
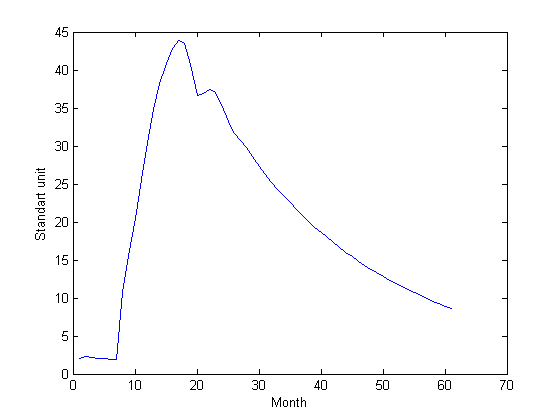
Рис. 1. Динамика дохода в кризисной ситуации в двумерном случае |
Рис. 2. Динамика капитала при кризисе в двумерном случае |
|
|
|
|
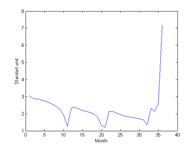
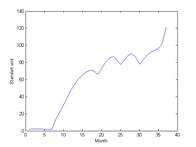
Рис. 3. Динамика инвестиций в ситуации роста в двумерном случае |
Рис. 4. Динамика капитала в ситуации роста в двумерном случае |
|
|
|
|
|
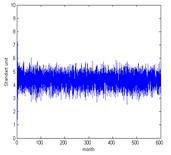
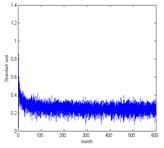
Рис. 5. Динамика дохода при динамическом хаосе |
Рис. 6. Динамика инвестиций при динамическом хаосе |
Рис. 7. Инвестиции как функция планового дохода |
Также представлены результаты численного моделирования со случайными параметрами системы. Данные графики получены при параметрах  ,
, 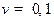 ,
,  ,
, 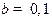 ,
, 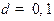 ,
,  ,
, 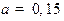 ,
, 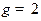 , e1=2, e2=2,
, e1=2, e2=2, 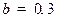 ,
,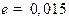 ,
, 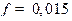 ,
,  ,
,  ,
, 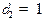 ,
, 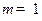 ,
, 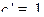 ,
, 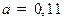 ,
, 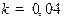 ,
,  ,
, 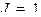 ,
, 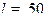 ,
, 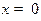 ,
,  , a - равномерно распределенная величина с математическим ожиданием 0, 055. Такой режим схож с динамическим хаосом. Он обладает свойствами перемежаемости и устойчивостью по Пуассону. Для демонстрации свойств данного режима, в данном случае осуществляем построение не на 36 месяцев, а на не вполне реалистичный период 500 месяцев.
, a - равномерно распределенная величина с математическим ожиданием 0, 055. Такой режим схож с динамическим хаосом. Он обладает свойствами перемежаемости и устойчивостью по Пуассону. Для демонстрации свойств данного режима, в данном случае осуществляем построение не на 36 месяцев, а на не вполне реалистичный период 500 месяцев.
Таким образом, в работе осуществлено моделирование достаточно крупных инвестиций в условиях рецессии. Показано, что даже в этом случае, и даже при наличии случайных внешних факторов, существуют сценарии устойчивого развития инвестиционных проектов.
дипломов


Оставить комментарий