ОСНОВНЫЕ  УРАВНЕНИЯ  ИЗГИБА  МНОГОСЛОЙНЫХ  ОРТОТРОПЫХ  ПЛАСТИН  НЕСИММЕТРИЧНОЙ  СТРУКТУРЫ

Мутовина  Наталья  Викторовна

канд.  техн.  наук,  ст.  преподаватель  кафедры  информационные  технологии  и  безопасность,  доцент  Карагандинского  государственного  технического  университета ,  Республика  Казахстан,  г.  Караганда

E-mail: 

Куанышев  Торехан  Тауфикович

студент   кафедры  информационные  технологии  и  безопасность,

Карагандинского  государственного  технического  университета,  Республика  Казахстан,  г.  Караганда

E-mail: 

MAIN  EQUATIONS  OF  THE  BEND  OF  MULTILAYERED  ORTOTROPY  PLATES  OF  ASYMMETRICAL  STRUCTURE

Mutovina  Natal ya

c andidate  of  Science,  senior  lecturer  of  Information  Technology  and  Security  department,  assistant  professor  of  Karaganda  state  technical  university,  Republic  of  Kazakhstan,  Karaganda

Kuanyshev  Torekhan

student  of  Information  Technology  and  Security  department,  Karaganda  state  technical  university ,  Republic  of  Kazakhstan,  Karaganda

АННОТАЦИЯ

Теории  многослойных  пластин,  уточняющие  техническую  теорию,  должны  учитывать  деформацию  в  поперечном  направлении  и  связанные  с  нею  факторы.  Полученные  уравнения  изгиба  многослойных  ортотропных  пластин  несимметричной  структуры  по  толщине  в  смешанной  форме  и  соответствующие  им  контурные  условия  представлены  в  конечно-разностной  форме  для  произвольного  узла  прямоугольной  сетки.

ABSTRACT

The  theories  of  multilayered  plates  specifying  the  technical  theory  have  to  consider  deformation  in  the  cross  direction  and  the  factors  connected  with  it.  The  received  equations  of  a  bend  multilayered  the  ortotropnykh  of  plates  of  asymmetrical  structure  on  thickness  in  the  mixed  form  and  the  planimetric  conditions  corresponding  to  them  are  presented  in  a  final  and  differential  form  for  any  knot  of  a  rectangular  grid.

Ключевые  слова:   ортотропные  слои;  несимметричная  структура;  многослойные  конструкции.

Keywords:   ortotropny  layers;  asymmetrical  structure;  multilayered  designs.

Рассмотрим  прямоугольную  в  плане  со  сторонами  а₁  и  а₂  (рисунок  1)  многослойную  пластину  с  ортотропными  слоями,  и  толщиной  H  =d₁+d₂,  состоящей  из  произвольного  количества  ортотропных  слоев._.  Пластину  отнесем  к  ортогональной  системе  координат  х₁,  х₂,  х₃  =  z.  Оси  х₁  и  х₂  лежат  на  координатной  плоскости  и  направления  их  совпадают  с  осями  ортотропии  слоев.  Координатную  плоскость  расположим  произвольно  по  высоте  сечения  пластины.  Расстояние  от  координатной  плоскости  до  нижней  и  верхней  поверхности  пластины  обозначим  соответственно  через.  d₁  и  d₂.  Нумерацию  слоев  производим  от  нижней  поверхности  пластины  (рисунок  2).  Общее  количество  слоев  обозначим  через  n,  тогда  принимает  k  =  1,  2,  3,  …,  n,  где  k  —  номер  произвольного  слоя.  Cлой,  в  котором  расположена  координатная  поверхность,  обозначим  через  m.  Все  слои  пластины  в  совокупности  по  толщине  образуют  пакет  слоев  [1].

В  общем  случае  предположим,  что  структуру  пакета  образуют  слои  различной  толщины  и  жесткости,  физико-механические  характеристики  которых  постоянны  по  их  толщине.  Количество  и  порядок  расположения  слоев  произвольны.

Считаем,  что  на  границе  при  переходе  от  слоя  к  слою,  выполняются  условия:

·     статические

    (1.1)

·     кинематические

  (1.2)

что  соответствуют  работе  их  слоев  без  проскальзывания  и  отрыва.

Пусть  на  верхней  площадке  пластины  действует  нормальная  нагрузка  q(х₁  х₂)  изменяющаяся  по  произвольному  закону,  положительное  направление  которой  совпадает  с  направлением  нормальной  оси  х₃  =  z.

На  поверхности  пластинки  граничные  условия  примут  вид:

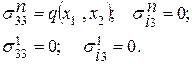  (1.3)

Рисунок  1.  Расчетная  схема  пластины

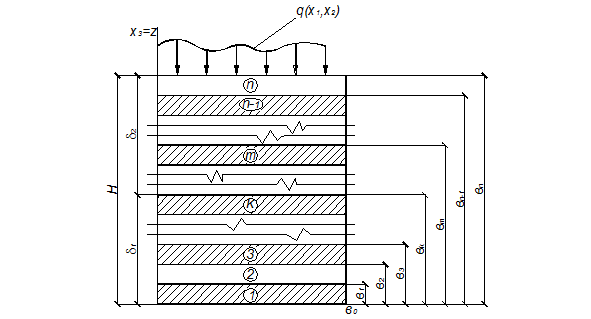
Рисунок  2.  Поперечный  разрез  многослойной  пластины

Условия  неразрывности  деформации  для  координатной  поверхности  имеют  вид  /100/:

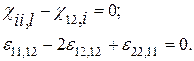    (1.4)

В  основу  уточненной  модели  напряженно-деформированного  состояния  многослойной  пластины  несимметричной  структуры  с  ортотропными  слоями,  положим  следующую  систему  гипотез: 

  (1.5)

Приведенные  гипотезы  получены  на  основе  гипотез,  предложенных  А.Ш.  Боженовым  /13/,  путем  пренебрежения  рядом  факторов,  несущественно  влияющих  на  напряженно-деформированное  состояние  пластин.

Здесь  W  и  c  —  искомые  функции  прогиба  и  сдвига  координатной  поверхности,  зависящие  от  координат  х  ₁  и  х  _2,    —  модуль  сдвига  материала  k-го  слоя  пластины,  остальные  компоненты  —  есть  функции  распределения,  зависящие  от  поперечной  координаты  z. 

Гипотезы  (1.5)  удовлетворяют  условиям  совместной  работы  слоев  без  отрыва  и  смещения,  условиям  на  поверхностях  пластины  и  определяют  нелинейный  закон  изменения  по  толщине  пластины  напряжений  поперечного  сдвига  и  нормальных  поперечных  напряжений.  Нормальные  перемещения  считаются  равными  прогибам  [2].

Для  функции  распределения  в  выражениях  (1.5)  имеем  следующие  формулы:

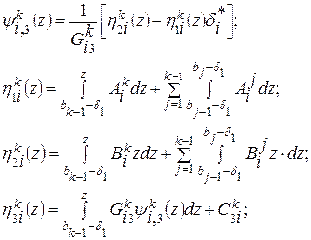    (2.6)

где  константы  имеет  вид:

    (2.7)

Для  компонент  формулах  (1.6)  и  (1.7)  имеем  следующие  выражения:

                  (2.8)

На  основе  принятых  гипотез  (1.5)  строим  линейную  геометрическую  модель  многослойной  пластины  и  устанавливаем  связь  между  напряжениями  и  деформациями  [3].

Для  этого  воспользуемся  некоторыми  известными  соотношениями  трехмерной  теории  упругости:

Соотношения  закона  Гука:

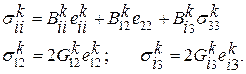           (2.9)

Обратные  выражения  закона  Гука:

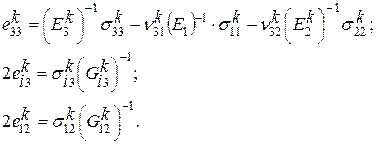    (1.10)

Соотношения  Коши:

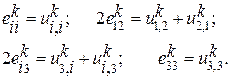  (1.11)

Деформацию  поперечного  сдвига  (x₁,  x₂,  z)  определим  из  закона  Гука  (1.9),  подставив  выражения  гипотезы  для  поперечных  касательных  напряжений  (1.5):

  (1.12) 

Нормальные  поперечные  деформации    найдем  из  последнего  соотношения  Коши  с  учетом  (2.5):

  (1.13)

Из  третьего  соотношения  Коши  (1.11),  выполнив  интегрирование  по  z  с  учетом  формул  (1.5)  и  (1.12)  получим  выражение  для  тангенциальных  перемещений:

  (1.14)

где  u_i(x₁  x₂)  —  функции  интегрирования,  являются  тангенциальными  перемещениями  координатной  поверхности  [4].

Функции  распределения    определяются  из  условий  удовлетворения  контакта  слоев  (1.2)  и  условий  на  координатной  поверхности 

  (1.15)

Тангенциальные  деформации  находим  из  первых  соотношений  Коши  (1.11)  подставляя  туда  (1.14):

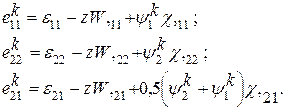    (1.16)

Компоненты  напряжений  обобщенного  закона  Гука  (1.9)  с  учетом  формул  (2.5)  и  (2.16)  выражаются  зависимостями:

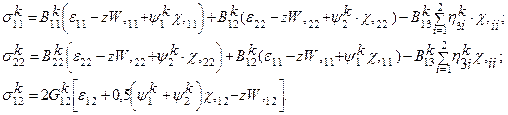    (1.17)

Выражения  перемещений  (1.5),  (1.14)  и  деформаций  (1.12),  (1.13),  (1.16)  позволяют  построить  геометрическую  модель  многослойных  ортотропных  пластин  и  определить  компоненты  напряженно-деформированного  состояния  НДС  в  произвольной  точке  k-го  слоя  [5].  В  рамках  принятых  гипотез  приближенно  удовлетворяются  все  15  уравнений  теории  упругости.

Таким  образом,  построенная  модель  описывает  трехмерный  закон  изменения  НДС  многослойных  пластин  несимметричной  структуры  по  толщине.  Модель  является  двумерной,  так  как  все  искомые  функции  являются  функциями  координатной  поверхности.

C писок  литературы:

1.Касимов  А.Т.  Алгоритм  расчета  многослойных  ортотропных  пластин  в  уточненной  постановке  //  IV  Междунар.  конф.  Наука  и  образование  —  ведущий  фактор  стратегии  «Казахстан-2030»,  посвящ.  10-летию  Независимости  Казахстана.  Тез.  докл.:  Караганда:  КарГТУ,  2001.  —  с.  22—24.

2.Касимов  А.Т.  Расчет  многослойных  ортотропных  прямоугольных  пластин  несимметричной  структуры  с  произвольным  закреплением  на  контуре  //  Пластины  и  оболочки:  Тр.  КарПТИ.  Караганда,  1992.

3.Рассказов  А.О.  Расчет  многослойной  ортотропной  пологой  оболочки  методом  конечных  элементов  //  Прикл.  механика,  —  1978.  —  т.  14.  —  №  8.  —  с.  51—56.

4.Рассказов  А.О.,  Соколовская  И.И.  Экспериментальное  исследование  статики  и  динамики  многослойных  пластин  //Прикл.механика.  —  1981.  —  т.  17.  —  №  12.  —  с.  65—70.

5.Юнусов  А.Ш.  Изгиб  слоистых  пластин  с  заполнителем  //Изв.ВУЗов  Строительство  и  архитектура.  1976.  №  4.