Статья опубликована в рамках: XXXVI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 27 августа 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
АЛГОРИТМ ОПТИМИЗАЦИИ ХАРАКТЕРИСТИК ФУНКЦИОНИРОВАНИЯ КОМПЬЮТЕРНЫХ СЕТЕЙ C НЕЧЕТКО ЗАДАННЫМИ ПАРАМЕТРАМИ
Шапорина Елена Леонидовна
Ассистент, кафедры компьютерных интеллектуальных систем и сетей Одесского национального политехнического университета, Украина, г. Одесса
Тишин Петр Метталинович
канд. техн. наук, доцент кафедры компьютерных интеллектуальных систем и сетей Одесского национального политехнического университета, Украина, г. Одесса
Милейко Игорь Генрикович
канд. техн. наук, доцент кафедры компьютерных интеллектуальных систем и сетей Одесского национального политехнического университета, Украина, г. Одесса
Шапорин Руслан Олегович
канд. техн. наук, доцент кафедры компьютерных интеллектуальных систем и сетей Одесского национального политехнического университета, Украина, г. Одесса
E-mail:
ALGORITHM OF OPTIMIZATION CHARACTERISTICS OF FUNCTIONING COMPUTER NETWORKS WITH FUZZY SETS PARAMETERS
Shaporina Olena
assistant department of computer intelligent systems and networks Odessa national polytechnic university, Ukraine, Odessa
Tishin Petro
PhD, associate professor department of computer intelligent systems and networks Odessa national polytechnic university, Ukraine, Odessa
Mileyko Igor
associate professor department of computer intelligent systems and networks Odessa national polytechnic university, Ukraine, Odessa
Shaporin Ruslan
PhD, associate professor department of computer intelligent systems and networks Odessa national polytechnic university, Ukraine, Odessa
АННОТАЦИЯ
В работе приведена однокритериальная задача оптимального распределения информационных потоков по каналам коммуникационных устройств с нечетко заданными данными. Приведено описание алгоритма решения задачи оптимизации в данной постановке.
ABSTRACT
In the paper, we present a one-criterion problem of optimal distribution of information flow through the channels of communication devices with clearly specified data. The description of the algorithm for solving the optimization problem in this setting.
Ключевые слова: сети массового обслуживания; среднее время задержки сообщения; нечеткие множества.
Keywords: queuing network; the average message delay time; fuzzy sets.
Современные компьютерные сети (КС) активно развиваются, используя новые информационные и телекоммуникационные технологии. И поэтому требуется разработка новых моделей их функционирования. Существующие модели функционирования КС основываются на использовании, как правило, точных значений сетевых параметров. На практике получение точных значений параметров для таких сложных систем, какими являются современные КС, представляется весьма трудоемкой задачей, что существенно усложняет использование данного класса моделей, поэтому в работе рассматривается построение моделей основных характеристик функционирования КС с использованием аппарата нечетких множеств. Использование данного подхода устраняет проблему получения четких значений сетевых параметров.
В работе коммуникационная система КС представляется в виде множества узлов коммутации (УК) [2, 3]. В качестве узлов коммутации рассматриваются коммутаторы и маршрутизаторы, на базе которых строятся коммуникационные системы современных КС. Для узлов коммутации (УК) сформированы показатели эффективности, которые используются в задачах анализа и синтеза рациональных структур КС. Один из основных показателей, который рассмотрен в данной работе, является среднее время задержки сообщений.
Моделью УК является узел, имеющий один входной канал по которой поступает входной поток заявок с интенсивностью l и n каналов связи выходящих из УК. При этом под одним входным потоком понимается суперпозиция всех входных потоков УК. Входной поток распределяется по n каналам связи и порождает в каждом канале трафик с интенсивностью lj, j=1,n.
Каждый канал связи рассматривается как система массового обслуживания с некоторой интенсивностью обслуживания mj, что позволяет множество каналов связи рассматривать как сеть систем массового обслуживания. Предполагается, что в сети действует стохастический алгоритм, управляющий распределением пакетов по каналам связи так, что из общего трафика l, поступающего на узел в j-й канал связи, выделяется некоторая доля pjl (1) и выполняется условие (2):
![]() (1)
(1)
 (2)
(2)
При решении данной задачи оптимизации важным показателем эффективности работы сети является среднее время задержки сообщения через узел которая определяется следующими соотношениями:
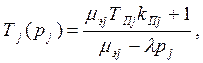 (3)
(3)
Параметры в выражении (3) определяются следующим образом:

 (4)
(4)
где: ![]() — средняя эквивалентная интенсивность обслуживания в j-м канале связи;
— средняя эквивалентная интенсивность обслуживания в j-м канале связи;
![]() — средняя интенсивность обслуживания в j-м канале связи;
— средняя интенсивность обслуживания в j-м канале связи;
![]() — средняя эквивалентная интенсивность старения информации в j-м канале связи;
— средняя эквивалентная интенсивность старения информации в j-м канале связи;
![]() — средняя интенсивность старения информации в j-м канале связи;
— средняя интенсивность старения информации в j-м канале связи;
![]() — коэффициент простоя j-го канала связи;
— коэффициент простоя j-го канала связи;
![]() — коэффициент готовности j-го канала связи;
— коэффициент готовности j-го канала связи;
![]() — коэффициент ненадежности j-го канала связи;
— коэффициент ненадежности j-го канала связи;
![]() — среднее время простоя;
— среднее время простоя;
![]() — среднее время исправной работы;
— среднее время исправной работы;
![]() — среднее время старения информации.
— среднее время старения информации.
Оптимизация состоит в выборе таких значений pj, при которых достигается минимальное значение показателя эффективности. Показатель, который позволяет оценить эффективность функционирования данной подсистемы, можно представить в виде:
 ;
;
С учетом выражения, приведённого выше, среднее время задержки сообщения через узел можно рассчитывать по следующему соотношению:
 , (5)
, (5)
где μэj = bj ,
![]()
Данные выражения дают возможность рассчитать оптимальное распределение трафика через выходные каналы КУ в случае, когда все исходные данные заданы точно. Однако такие параметры, как время простоя ![]() , время исправной работы
, время исправной работы ![]() и время старения информации
и время старения информации ![]() в j-м канале связи часто не могут быть определены точно. Некоторые вопросы по решению однокритериальных оптимизационных задач, в случае, когда характеристики функционирования компьютерных или телекоммуникационных систем являются нечеткими, рассматривались в работах [4, 8, 9]. В общем случае решение этой задачи рассмотрено ниже.
в j-м канале связи часто не могут быть определены точно. Некоторые вопросы по решению однокритериальных оптимизационных задач, в случае, когда характеристики функционирования компьютерных или телекоммуникационных систем являются нечеткими, рассматривались в работах [4, 8, 9]. В общем случае решение этой задачи рассмотрено ниже.
Для учёта нечеткости исходных данных представим их в виде нечетких величин, которые определены каждая на своем полном ортогональным семантическим пространстве (ПОСП) [6], с функциями принадлежности трапецеидального типа, удовлетворяющими соотношениям [9]:
![]() ,
, ![]() ,
, ![]() , (6)
, (6)
Здесь через ![]() ,
, ![]() ,
, ![]() , обозначаются ПОСП для параметров
, обозначаются ПОСП для параметров ![]() ,
, ![]() ,
, ![]() . Вследствие нечеткого описания величин, функции принадлежностей которых описаны соотношением (6), величины, описанные соотношением (4), являются нечеткими переменными, функции принадлежностей которых можно вычислить с помощью математических операций приведенных [4, 8, 9].
. Вследствие нечеткого описания величин, функции принадлежностей которых описаны соотношением (6), величины, описанные соотношением (4), являются нечеткими переменными, функции принадлежностей которых можно вычислить с помощью математических операций приведенных [4, 8, 9].
Полученные нечеткие величины будут иметь также трапецеидальные функции принадлежности, которые можно описать соответствующими четверками значений:
 (7)
(7)
При этом из соотношений (4) получается справедливость следующих зависимостей:
|
|
(8) |
Можно показать, что параметры из выражения (3) будут представлять собой нечеткие величины с трапецеидальными функциями принадлежности.
С другой стороны для решения оптимизационной задачи с нечеткими величинами требуется ввести ПОСП ![]() и ПОСП
и ПОСП ![]() для параметров bj и βj , которые могут быть рассчитаны на основании формул (7) с помощью соотношений:
для параметров bj и βj , которые могут быть рассчитаны на основании формул (7) с помощью соотношений:
![]()
![]() (9)
(9)
Термы в ПОСП Пb в дальнейшем обозначаем через ![]() а термы в ПОСП Пβ через
а термы в ПОСП Пβ через ![]() , где Nb — число термов в ПОСП Пb, а Nβ — число термов в ПОСП Пβ .
, где Nb — число термов в ПОСП Пb, а Nβ — число термов в ПОСП Пβ .
Для оценки величины ![]() введем величину
введем величину ![]() :
:
 (10)
(10)
для которой, в свою очередь, вводится соответствующий ПОСП ![]() .
.
Определим метрику, которая позволяет значениям ![]() и
и ![]() ставить в соответствие термы в ПОСП Пb и ПОСП Пβ . Для этого, аналогично тому, как это делалось в работе [8] введём в рассмотрение функцию
ставить в соответствие термы в ПОСП Пb и ПОСП Пβ . Для этого, аналогично тому, как это делалось в работе [8] введём в рассмотрение функцию ![]() следующим соотношением:
следующим соотношением:
 (11)
(11)
где нечеткое число ![]() определяется четверкой
определяется четверкой ![]() , нечеткое число
, нечеткое число ![]() четверкой
четверкой ![]() , а функции
, а функции ![]() , когда
, когда ![]() , также как и в работе [3].
, также как и в работе [3].
В этом случае значения нечётких параметров bj и βj можно рассчитать с учетом соотношений (11).
![]()
![]()
Нечёткое значение среднего времени задержки сообщений будет определяться выражением:
![]() (12)
(12)
Причем согласно свойствам ПОСП на Пb, Пβ и ПT естественно вводится отношения частичного порядка , которое упорядочивает множества термов входящих в каждое из данных ПОСП.
Однокритериальную оптимизационную задачу, в рассматриваемом случае можно сформулировать следующим образом:
Определить четкие значения pj для которых величина принимает минимальное значение в смысле отношения частичного порядка .
Таким образом однокритериальная оптимизационная задача сводится к определению четких значений , при которых величина ![]() определяемая формулой (12) принимает минимальное значение в смысле отношения частичного порядка . Для определения данных величин введем в рассмотрение величины
определяемая формулой (12) принимает минимальное значение в смысле отношения частичного порядка . Для определения данных величин введем в рассмотрение величины ![]() и
и ![]() , которые получаются в результате операции дефаззификации величин и , а также обозначим через
, которые получаются в результате операции дефаззификации величин и , а также обозначим через ![]() множество каналов для которых
множество каналов для которых ![]() принадлежат , а через
принадлежат , а через ![]() каналов для которых
каналов для которых ![]() принадлежат . Обозначим через
принадлежат . Обозначим через ![]() , а через
, а через ![]() — их количество. Используя введенные обозначения для определения величин и величины
— их количество. Используя введенные обозначения для определения величин и величины ![]() определяемой формулой (12) предлагается следующий алгоритм решения однокритериальной задачи.
определяемой формулой (12) предлагается следующий алгоритм решения однокритериальной задачи.
1. Ввод исходных параметров ,,, μj.
2. Определить нечёткие значения параметров , , .
3. Задать количество термов и параметры трапецеидальных функций принадлежности каждого терма на ПОСП , ПОСП и ПОСП .
4. Построить , , .
5. Задать количество термов и параметры трапецеидальных функций принадлежности каждого терма на ПОСП и ПОСП .
6. Построить ПОСП , .
7. Выполнить операции дефаззификации для параметров ![]() и
и ![]() :
: ![]() и
и ![]() .
.
8. Определить величины ![]() и множества
и множества ![]() .
.
9. Задать r=1.
10. Для даного r вычисляем суммы:
![]()
![]()
![]() .
.
11. Если ![]() <1, то r=r+1 и перейти к п.10, иначе к п. 12
<1, то r=r+1 и перейти к п.10, иначе к п. 12
12. Полагаем ![]() .
.
13. Вычислить параметры ![]() , при этом для всех
, при этом для всех ![]() справедливо соотношение
справедливо соотношение

14. Расчет трапецеидального нечеткого числа
15. Конец.
В работе приведена нечеткая модель расчета среднего времени задержки сообщения через коммуникационные узлы в КС, при этом каждый канал УК моделируется в виде сети массового обслуживания. Сформулирована однокритериальная задача оптимального распределения информационных потоков по каналам КУ с нечетко заданными данными. Приведено описание алгоритма решения задачи оптимизации в данной постановке.
1.Дилигенский Н.В., Дымова Л.Г., Севастьянов П.В. Нечеткое моделирование и многокритериальная оптимизация производственных систем в условиях неопределенности: технология, экономика, экология // Москва: «Издательство Машиностроение — 1», 2004, — 397 с.
5.Метод расчета размеров буферов коммутаторов / Шапорин Р.О., Шапорин В.О., Милейко И.Г.// Труды Одесского политехнического университета, — № 2(28), — 2007 — С. 116—119.
6.Метод расчета параметров коммуникационного оборудования сети передачи данных / Шапорин Р.О., Плачинда О.Е. // Вісник національного технічного університету "ХПІ". Збірник наукових праць. Тематичний випуск: Нові рішення в сучасних технологіях, м. Харків, — № 23, — 2011 — С. 111—114.
дипломов





Оставить комментарий