Статья опубликована в рамках: XXXIX Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 26 ноября 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
НЕУСТОЙЧИВЫЕ РЕЖИМЫ ТРАНСЗВУКОВОГО ТЕЧЕНИЯ В КАНАЛЕ С ИЗГИБОМ
Матюхина Ирина Анатольевна
программист Крыловского государственного научного центра, РФ, г. Санкт-Петербург
E -mail: imatyuhina@inbox.ru
Кузьмин Александр Григорьевич
д-р физ.-мат. наук, С-Петербургский государственный университет, РФ, г. Санкт- Петербург
E-mail:
UNSTABLE REGIMES OF TRANSONIC FLOW IN A BENDED CHANNEL
Irina Matyukhina
programmer, Krylov State Research Center, Russia, St. Petersburg
Alexander Kuzmin
Dr.Sc., St.Petersburg State University, Russia, St. Petersburg
АННОТАЦИЯ
Проведено численное исследование двумерного турбулентного потока в канале при заданной сверхзвуковой скорости на входе. Вследствие изогнутости канала в его средней части формируется криволинейная ударная волна и зона дозвуковых скоростей. Далее скорость потока возрастает и становится снова сверхзвуковой. Решения нестационарных уравнений Навье-Стокса, осредненных по Рейнольдсу, получены с помощью вычислительной программы, основанной на методе конечных объемов. Показано наличие гистерезиса зависимости положения ударной волны от числа Маха Min >1, заданного на входе в канал.
ABSTRACT
2D turbulent flow in a channel with a given supersonic velocity at the inlet is studied numerically. Due to the bend of the channel, a curved shock wave and a subsonic zone form in the midpart of the channel. Downstream of the subsonic region, the flow velocity rises to supersonic values again. Solutions of the unsteady Reynolds-averaged Navier-Stokes equations are obtained with a finite-volume solver. The existence of a hysteresis in the dependence of the shock wave position on the inlet Mach number Min>1 is studied.
Ключевые слова: ударная волна; звуковая линия; местные сверхзвуковые зоны; неустойчивость.
Keywords: shock wave; sonic line; local supersonic regions; instability.
1. Введение. Торможение сверхзвукового потока в воздухозаборниках со смешанным сжатием осуществляется в системе ударных волн, расположенных перед минимальным поперечным сечением, где скорость потока становится дозвуковой [3]. В минимальном сечении происходит ускорение потока вновь до сверхзвуковых скоростей, в результате чего формируется вторая сверхзвуковая зона. Недавние исследования обтекания аэродинамических профилей [1] показали, что слияние или расщепление сверхзвуковых зон сопровождается резкими изменениями значений коэффициента подъемной силы. Это обусловлено тем, что картина обтекания, в которой две сверхзвуковые зоны касаются в одной точке, может быть только нестационарной. Следовательно, релаксация во времени должна приводить к более глубокому слиянию сверхзвуковых зон или к их расхождению на конечное расстояние друг от друга. Это явление было изучено в [2] в случае турбулентного трансзвукового течения в канале при разных профилях скорости во входном сечении. В данной работе продолжено изучение неустойчивого взаимодействия сверхзвуковых зон, при этом размеры канала уменьшены до значений, подходящих для проведения экспериментальных исследований в аэродинамической трубе.
2. Постановка задачи и численный метод. Рассматривается течение воздуха в канале длины 0,48 м с входным сечением x=0, 0<y<0,3 м. Нижняя стенка канала имеет излом в точке x=0,2 м, y=0, а верхняя – в точке x=0,16 м, y=0,31 м. Выходным сечением является отрезок с верхней и нижней кромками, координаты которых x=0,48 м, y=0,2514 м и x=0,26, y=−0,02 м.
На входе в канал заданы значения компонент скорости потока, статическое давление pin=100000 н/м2 , а также статическая температура Tin=250 K, которой соответствует скорость звука ain=317,02 м/с при показателе адиабаты 1,4. На выходе ставится условие сверхзвуковой скорости истечения, а на стенках канала — условия прилипания и отсутствия теплового потока. В качестве начальных данных для параметров потока в канале использовались параметры во входном сечении или поле течения, полученное для некоторого предыдущего значения Мin.
Численные решения системы уравнений Навье-Стокса находились с помощью вычислительной программы ANSYS CFX-15 второго порядка точности на неструктурированных сетках с числом ячеек свыше 4´105. Использовалась модель турбулентности k-ω SST, которая хорошо описывает турбулентные течения в условиях отрыва пограничного слоя от гладких поверхностей. Тестирование программы проводилось на задаче обтекания трансзвуковым потоком профиля RAE 2822 [4].
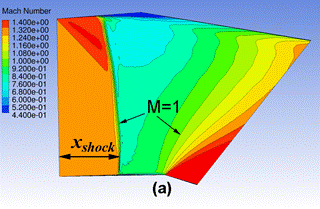
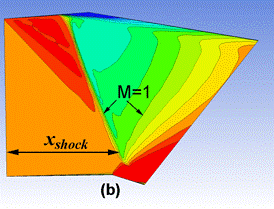
Рисунок 1. Изомахи в канале при задании постоянной скорости потока (1) во входном сечении: a ) Min=1,278, b) Min=1,280
3. Результаты расчетов. Было проведено исследование положения ударной волны в канале при разных значениях скорости потока на входе в канал. В первом варианте исходных данных задавалось постоянное значение горизонтальной и вертикальной компонент скорости:
U in=Minain, Vin=0. (1)
На рис. 1,а представлены полученные линии постоянного числа Маха в канале при Min=1,278. При этом сверхзвуковые зоны находятся на конечном расстоянии друг от друга. С увеличением Min до 1,28 происходит резкое слияние местных сверхзвуковых зон, см. рис. 1,б.

Рисунок 2. Зависимость координаты x s ударной волны в канале от Min при задании скорости потока во входном сечении по формулам:(1) — кривая 1; (2) — кривая 2
В качестве параметра, характеризующего положение ударной волны, использовалась координата xshock ударной волны на высоте y= 0,05 м. Расчеты показали, что постепенное уменьшение Min от 1,280 до 1,238 приводит к смещению ударной волны в направлении к входному сечению канала, так что значение xshock плавно уменьшается до 0,1849 м (см. верхнюю часть графика 1 на рис. 2). При этом качественная картина течения не изменяется. Однако с уменьшением Min до 1,235 происходит расщепление сверхзвуковой области на две части и релаксация к стационарному состоянию с двумя сверхзвуковыми зонами, расположенными на расстоянии 0,195 м друг от друга. При последующем постепенном увеличении Min от 1,235 до 1,278 ударная волна смещается вниз по течению, и реализуется снова картина течения, показанная на рис. 1а.
Во втором варианте граничных условий на входе в канал была задана переменная по высоте скорость потока
U in(y)=Min ain cos(y qwall /0,3) , Vin(y)= Min ain sin(y qwall /0,3) , (2)
где: qwall = atan(1/16) — угол наклона верхней стенки канала к оси x при 0<x<0,16 м. Согласно (2) направление вектора скорости во входном сечении совпадает с направлением стенок канала при y=0 и y= 0,3 м.
График 2 на рис. 2 показывает результаты расчетов координаты xshock ударной волны при изменениях параметра Min в условиях (2). Верхняя часть графика показывает постепенное уменьшение величины xshock с уменьшением Min от 1,26 до 1,20. Затем происходит расщепление сверхзвуковой зоны и быстрое перемещение ударной волны вверх по течению к входному сечению канала. Для предотвращения выброса ударной волны из канала, значение Min увеличивалось в ходе релаксации до 1,227, как показано левой пунктирной линией на рис. 2. Последующее постепенное увеличение Min до 1,256 приводило к смещению ударной волны вниз по течению до координаты xshock = 0,1244 м (см. нижнюю часть графика 2 на рис. 2).
Данная работа выполнена с использованием вычислительных ресурсов Ресурсного Центра “Вычислительный центр СПбГУ” (http://cc.spbu.ru).
Список литературы:
1.Кузьмин А.Г. Бифуркации течения при трансзвуковом обтекании простых профилей с эллиптической и клиновидной носовыми частями // Журнал Прикладной Механики и Технической Физики. — 2010. — Т. 51. — № 1, — с. 22—28.
2.Кузьмин А., Матюхина И. Бифуркации турбулентного течения в канале при взаимодействии сверхзвуковых зон // Технические науки — от теории к практике / Сб. ст. по материалам XXXVIII междунар. науч.-практ. конф. — 2014 — 9 (34). Новосибирск: Изд. «СибАК», — с. 79—84.
3.Krushnarao Kotteda V.M., Mittal S. Viscous flow in a mixed compression intake // Internat. J. for Numerical Methods in Fluids. — 2011. — Vol. 67, — pp. 1393—1417.
4.Kuzmin A. Transonic flow past a Whitcomb airfoil with a deflected aileron // Internat. J. of Aeronautical and Space Sciences. — 2013. — Vol. 14, — № 3, — pp. 210—214.
дипломов


Оставить комментарий