КЛАССИФИКАЦИЯ  ГАЗОДИНАМИЧЕСКИХ  РАЗРЫВОВ  И  ЗАДАЧ  ОБ  ИХ  ИНТЕРФЕРЕНЦИИ

Ильина  Тамара  Евгеньевна

аспирант,  Университет  ИТМО,  РФ,  г.  Санкт-Петербург

E -mail:  tamara-190@yandex.ru

Булат  Павел  Викторович

канд.  физ.-мат.  наук,  руководитель  лаборатории  «НМНКБС»,  Университет  ИТМО,  РФ,  г.  Санкт-Петербург

E-mail: 

CLASSIFICATION  OF  GAS-DYNAMIC  DISCONTINUITIES  AND  THEIR  INTERFERENCE  PROBLEMS

Tamara  Ilina

postgraduate  student,  ITMO  University,  Russia,  Saint  Petersburg

Pavel  Bulat

candidat  of  scince,  head  of  the  Laboratory  "NMNKBS",  ITMO  University,  Russia,  Saint  Petersburg

АННОТАЦИЯ

Рассмотрена  классификация  газодинамических  разрывов,  ударно-волновых  процессов,  ударно-волновых  структур,  задач  о  взаимодействии  разывов.  Рассмотрены  различные  классификационные  признаки:  термодинамические,  кинематические,  нестационарность,  направление  разрыва,  приходящие  и  исходящие  разрывы.  Исследования  выполнены  при  финансовой  поддержке  Министерства  образования  и  науки  РФ  (Соглашение  №  14.575.21.0057).

ABSTRACT

We  have  considered  the  classification  of  gas-dynamic  discontinuities,  shock-wave  processes,  shock-wave  structures,  discontinuity  interaction  problems.  We  have  considered  different  classification  criteria:  thermodynamic,  cinematic,  transiency,  discontinuity  direction,  arriving  and  outgoing  discontinuities.  The  researches  are  executed  with  the  financial  support  of  the  Ministry  of  Education  and  Science  of  the  Russian  Federation  (the  Agreement  №  14.575.21.0057). 

Ключевые  слова:   скачок;  ударная  волна;  простые  волны;  волны  Римана;  интерференция  газодинамических  разывов.

Keywords:   jump;  shock  wave;  simple  waves;  Riеmann  waves;  gas-dynamic  discontinuity  interference.

Введение

Традиционно,  под  ударно-волновым  процессом  (УВП)  будем  понимать  процессы  преобразования  газодинамических  переменных  в  волнах  и  разрывах.

Переменные    представляют  собой  множества  параметров  кинематических  (u  —  скорость,  w  —  ускорение),  термодинамических  (p  —  давление,  ρ  —  плотность,  t  —  температура),  f_o  —  параметров  торможения,  изменения  энтропии  ΔS  =  Cvlnϑ/ϑ  ,  где  ϑ  =  p/p^γ  –  инвариант  Лапласа-Пуассона,  и  h  и  h₀  —  энтальпии,  а  также  и  теплофизических  параметров  (теплоемкости  c_p  и  c_v,  γ  =  c_p/c_v  —  показатель  адиабаты,  вязкости  и  пр.),  которые  могут  изменяться  в  ходе  УВП.

Ставится  задача  выполнить  классификацию  возможных  типов  взаимодействия  всех  видов  волн  и  газодинамических  разрывов.  Напомним  краткие  сведения  о  газодинамических  разрывах  (ГДР).  Как  известно,  сверхзвуковые  течения  могут  содержать  области,  где  параметры  меняются  резко,  скачком.  В  рамках  модели  идеального  газа  в  таких  случаях  говорят  о  существовании  газодинамических  разрывов.

Газодинамические  разрывы   в  сверхзвуковых  течениях  бывают  нулевого  порядка  Ф₀:  центр  волны  разрежения/сжатия,  скачок  уплотнения  и  поверхность  скольжения,  на  которых  терпят  разрыв  газодинамические  параметры  течения  (давление  P,  полное  давление  Р₀,  скорость  u,  угол  наклона  вектора  скорости  ϑ)  и  первого  порядка,  называемые  также  слабыми  разрывами  (разрывные  характеристики,  слабые  тангенциальные  разрывы)  Ф₁,  на  которых  терпят  разрыв  первые  производные  газодинамических  переменных.  Можно  определить  особенности  (разрывы)  Ф_i  пространства  газодинамических  переменных  любого  порядка.

Условия  динамической  совместности  (УДС)   на  ГДР  Ф₀  [15],  связывающие  параметры  течения  до  разрыва  и  за  ним,  выводятся  из  законов  сохранения  потока  вещества,  потока  энергии,  компонент  потока  импульса,  записанных  перед  разрывом  и  за  ним.  В  качестве  параметра  в  этих  соотношениях  выступает  интенсивность  разрыва  J  (чаще  всего  она  определяется  как  отношение  давления  за  разрывом  к  давлению  перед  ним). 

Дифференциальные  условия  динамической  совместности  (ДУДС)   Ф₀  связывают  неравномерности  течения  перед  скачком  и  за  ним  [16] 

  (1)

Коэффициенты  А_ij,  с_i  опубликованы  в  работах  В.Н.  Ускова  [16,  9].  В  целях  общности  в  уравнения  добавлены  N₄=^тм/y  (^тм=0  в  плоском  течении)  и  N₅=K_i  (кривизна  скачка  уплотнения).  ДУДС  по  известному  полю  течения  перед  скачком,  интенсивности  и  кривизне  скачка  позволяют  найти  производные  от  газодинамических  переменных  за  скачком  [17].  Если  же  одна  из  неравномерностей  известна,  то  можно  найти  кривизну  скачка  в  заданной  точке.  Это  позволяет  в  ряде  случаев  производить  расчет  поля  течения,  явно  выделяя  газодинамические  разрывы,  вычисляя  их  геометрию  с  помощью  ДУДС.  Например,  на  границе  сверхзвуковой  струи,  истекающей  из  сопла  Лаваля  в  покоящуюся  атмосферу,  N₁=0,  это  позволяет  вычислить  кривизну  границы  струи  на  кромке  сопла  [2;  10].

УДС  и  ДУДС  позволяют  составить  полный  перечень  возможных  конфигураций  взаимодействующих  ГДР,  а  также  исследовать  область  их  существования.  Этому  посвящена  фундаментальная  монография  [9],  в  которой  впервые  в  современном  виде  сформулирована  законченная  теория  интерференции  стационарных  ГДР.

1.  Классификация  разывов

1.1.Классификация  по  термодинамическому  принципу

Важным  термодинамическим  отличием  простых  волн  и  разрывов  является  поведение  энтропии  в  потоках,  проходящих  через  них.  Основным  параметром  таких  волн  является  отношение  статических  давлений  (интенсивность  разыва)    за  волной  и  до  волны. 

Отношение  плотностей    связывается  с  интенсивностью  волны  через  изоэнтропу  (инвариант)  Лапласа-Пуассона  (ϑ  =  const),  то  есть

  (2)

или  через  ударную  адиабату  Ренкина-Гюгонио

  (3)

Первый  случай  определяет  изоэнтропические  акустически  (звуковые),  волны  типа  Римана    или  Прандтля-Майера  .  Второй  —  ударные  неизоэнтропические  волны  . 

Волны  разрежения  и  уплотнения  (сжатия).   Волны  делятся  на  волны  разрежения  (J  ≤  1)  и  уплотнения  (J  >  1).  К  последним  относятся  изоэнтропические  волны  сжатия  (  and  )  и  ударные    волны. 

Волны  сильные  и  слабые.   Если  значения  интенсивности  J  ≠  1,  то  волна  называется  сильной.  В  вырожденной  волне  (J  =  1)  сами  газодинамические  переменные  не  изменяются,  но  на  таком  слабом  разрыве  могут  изменятся  производные  этих  переменных.  Слабыми  разрывами  (разрывными  характеристиками)  являются  передние  и  задние  фронты  изоэнтропических  волн  и  вырождающиеся  в  них  сильные  разрывы  (J  →  1).  На  слабых  разрывах  могут  изменяться  не  только  первые  производные  (f′),  но  и  производные  более  высокого  порядка.  Все  возможные  типы  волн  и  разрывов  сведены  в  таблицу  1.

Таблица  1.

1.2. Классификация  по  кинематическому  принципу

По  кинематическому  принципу  волны  и  ГДР  делятся  на  стационарные  и  нестационарные.  К  первым  относятся  образующиеся  в  сверхзвуковых  потоках  волны  (рис.  1  а)  типа  Прандтля-Майера  ()  и  скачки  уплотнения  (σ)  (стоячие  ударные  волны,  рис.1б).  Фронты  (передний  и  задний  у  ()  волн)  и  поверхность  скачка  неподвижны  в  сверхзвуковых  потоках  газа,  которые  проходят  через  них.

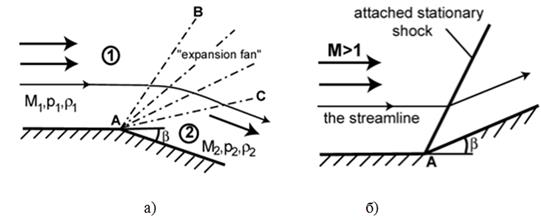
Рисунок  1.  Волна  Прандтля-Майера  (а)  и  стационарный  скачок  уплотнения

У  бегущих  волн  Римана  и  в  ударных  волнах  фронты  перемещаются  в  пространстве  и  во  времени.  В  стационарных  и  нестационарных  разрывах  по  разному  выглядит  связь  отношения  полных  давлений  J₀=p₀₂/p₀₁  и  полных  теплосодержаний  H₀=h₀₂/h₀₁  [7].  В  установившихся  потоках  H₀=1  соотношение  принимает  вид

.  (4)

Формула  (4)  описывает  коэффициент  потерь  полного  давления  в  сверхзвуковых  установившихся  волнах  (скачки  уплотнения    и  в  изоэнтропических  волнах  Прандтля-Майера,  где  JE^γ=1).

В  нестационарных  течениях  полная  энтальпия  изменяется  ,  поэтому  в  волнах  Римана  и  бегущих  ударных  волнах  изменения    и    связаны  между  собой  формулой

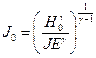  ,  (5)

причем  наиболее  просто  в    волнах

  .  (6)

1.3.Классификация  по  направлению  движения  фронта  волны

Направления  движения  одномерных  волн  по  исходному  потоку  газа  можно  характеризовать  показателем    направления  движения  фронта.

При    фронты  движутся  в  направлении  движения  исходного  потока,  и  волны  называются  спутными.  Скорости  фронтов  изоэнтропных  волн  относительно  частиц  потока  являются  звуковыми  и  имеют  скорость  распространения  u  +  a  (а  —  скорость  звука).  Фронт  прямой  ударной  волны  имеет  скорость  D  >  a  и  обгоняет  частицы  исходного  потока.

Значения    соответствуют  встречным  волнам,  фронты  которых  движутся  навстречу  исходному  потоку.  Поскольку  передние  фронты  простых  волн  относительно  частиц  газа  движутся  со  скоростью  звука,  то  в  сверхзвуковом  исходном  потоке  (u  >  a)  они  встречают  частицы  потока,  но  сносятся  вниз  по  нему.  Такие  волны  будем  называть  дрейфующими  (сносимыми).

Таким  образом,  по  направлению  движения  волны  относительно  потока  можно  разделить  на:  спутные,  сонаправленые  потоку,  и  встречные  волны.  Встречные  простые  волны,  распространяющиеся  по  сверхзвуковому  потоку,  являются  дрейфующими. 

Если  скорость  распространения  ударной  волны  меньше  скорости  набегающего  на  нее  сверхзвукового  потока,  то  такая  волна  будет  также  дрейфующей  (сносимой). 

Частным  случаем  дрейфующей  ударной  волны  является  прямой  скачок  уплотнения,  который  называется  также  стоячей  ударной  волной.

1.4. Классификация  ударно-волновых  структур  (УВС)

В  ударно-волновых  процессах  могут  участвовать  не  только  одиночные  волны  и  разрывы,  но  и  их  системы  и  ударно-волновые  структуры  (УВС).  Под  ударно-волновыми  системами  (структурами)  понимаются  совокупности  нескольких  волн  и  разрывов,  через  которые  последовательно  проходят  линии  тока  или  траектории  частиц  в  установившихся  или  нестационарных  течениях.  УВС  часто  используются  для  управления  газодинамическими  параметрами  потоков  газа,  с  помощью  которых  решаются  различные  прикладные  задачи  аэрогазодинамики.  Для  этого  в  исходных  потоках  специально  создаются  системы  волн  или  скачков  с  оптимальными  для  решаемой  задачи  свойствами.  Типичным  примером  являются  системы  скачков  уплотнения  (рис.  2)  в  сверхзвуковых  воздухозаборниках  самолетов  [8].

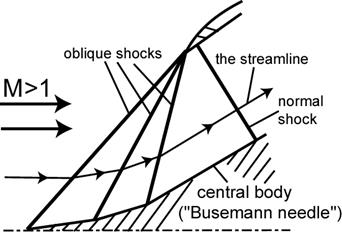
Рисунок  2.  Оптимальная  УВС  в  воздухозаборнике

Ударно-волновые  структуры  возникают  в  результате  взаимодействия  (пересечения,  интерференции)  волн  или  разрывов  между  собой,  с  тангенциальными,  контактными,  свободными  или  твердыми  поверхностями. 

Различают  догоняющие,  встречные  разрывы,  распады  или  ветвления  разрывов  [15]. 

По  отношению  к  точке,  в  которой  образуется  УВС,  разрывы  делятся  на  приходящие  и  исходящие,  что  особенно  важно  при  изучении  причин  распада  произвольного  разрыва.  Причиной  образования  структур  являются  приходящие  в  одну  точку  волны  и  разрывы.  Исходящие  волны  (разрывы)  представляют  собой  следствие  взаимодействия  приходящих  волн  (разрывов).  Из  взаимодействия  изоэнтропических  волн  исходящими  могут  быть  только  центрированные  волны  разрежения  (  или  ),  центры  которых  совпадают  с  точкой  пересечения  приходящих  волн.  Центры  волн  сжатия  образуются  пересечением  характеристик  одного  семейства  с  возникновением  в  этой  точке  ударно-волновой  структуры. 

В  образующихся  структурах  линии  тока  проходят  различные  системы  приходящих  и  исходящих  волн.  Типичным  примером  являются  тройные  конфигурации  (ТК),  состоящие  из  одного  приходящего  σ₁  и  двух  исходящих  σ₂,  σ_с  нормальных  разрывов  (рис.  3),  разделенных  тангенциальным  разрывом  . 

Рисунок  3.Тройная  конфигурация  ударных  волн

На  рисунке  3  σ₁  —  скачки  уплотнения,  из  которых  —  приходящий  скачок,  который  разветвляется  на  скачки  (2)  и  (c),  если  за  ними  течения  сверхзвуковые.  В  ударно-волновых  структурах  часть  линий  тока  последовательно  проходят  через  систему  волн  (1)  и  (2),  а  другая  часть  —  только  через  волну  (c).  Решение  задач  о  расчете  структур  обычно  строится  на  условиях  динамической  совместности  на  тангенциальном  (либо  контактном)  разрыве.

2.  Классификация  задач  о  взаимодействии  волн  и  разрывов

2.1. Классификация  по  газодинамическому  признаку

По  газодинамическим  признакам  волны  могут  быть  разделены  на  два  рода:  изоэнтропические  волны  и  разрывы.  Тогда  можно  выделить  три  типа  взаимодействия  волн  [11]:

1.  пересечение  газодинамических  разрывов,  к  которым  относятся  ударные  волны  и  контактные  разрывы,  между  собой;

2.  взаимодействие  изоэнтропных  волн  Римана  между  собой;

3.  взаимодействие  изоэнтропных  волн  с  газодинамическими  разрывами.

Кроме  того,  волны  и  разрывы  могут  взаимодействовать  с  твердымим  поверхностями.

Энтропийные  волны  (контактные  разрывы)  между  собой  пересекаться  не  могут,  поэтому  к  первому  типу  относятся  взаимодействия  ударных  волн  между  собой  или  с  контактными  разрывами.  Процесс  взаимодействия    или    —  волны  с  контактным  разрывом  называется  рефракцией,  и  его  причину  можно  обозначить  как  сумму  приходящих  волн:    или  .  Данный  процесс  сопровождается  преломлением  и  отражением  волн  на  контактном  разрыве.  Рефракция    относится  к  взаимодействию  газодинамических  разрывов,  а  рефракция    —  к  смешанному  типу.  Остальные  случаи  взаимодействия  волн  называются  интерференцией  ().

2.2.Размерность  задачи  и  обощенная  ударно-волновая  структура

С  точки  зрения  размерности,  время  t  является  такой  же  координатой,  как  и  пространственные  координаты.  В  этом  смысле  одномерная  нестационарная  центрированная  волна  Римана  полностью  эквивалентна  плоской  стационарной  волне  Прандтля-Майера  (рис.  1а).  Косой  скачок  уплотнения  эквивалентен  бегущей  одномерной  D-волне.  Криволинейный  скачок  уплотнения  эквивалентен  D-волне,  движущейся  с  ускорением.

Существуют  разные  подходы  к  построению  классификаций  ударно-волновых  структур  и  их  взаимодействий.  В.Н.  Усковым  в  1979  г.  была  предложена  классификация  на  основе  обобщенной  УВС  [12].  Обобщенная  УВС  составлена  из  всех  возможных  типов  разрывов  и  волн:  трех  приходящих,  одного  главного,  одного  тангенциального  и  одного  отраженного  разрывов  (рис.4).  Последний,  может  быть  как  скачком  уплотнения,  так  и  волной  разрежения.  Данная  классификация  является  неполной,  т.  к.  не  включает  простые  волны.  Пропущен  и  центр  центрированной  волны  сжатия,  который  также  является  разрывом. 

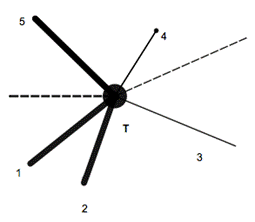
Рисунок  4.  Обобщенная  ударно-волновая  структура.  1—2  приходящие  скачки  уплотнения  одного  направления,  3  —  отраженный  разрыв  (скачок  или  волна),  4  —  главный  исходящий  разыв,  5  —  приходящий  встречный  скачок  уплотнения.  -  -  -  —  тангенциальные  разрывы

Тем  не  менее,  для  частного  случая  размерности  2  обобщенная  УВС  допускает  введение  исчерпывающей  классификации  задач  об  интерференции.  По  отношению  к  точке  интерференции  Т  (рис.  4)  газодинамические  разрывы  в  обобщенной  УВС  делятся  на  приходящие  (R_a)  и  исходящие  (R_p).  У  приходящих  разрывов  составляющая  вектора  скорости  на  направление  разрыва  направлена  к  точке  Т,  а  у  исходящих  —  от  нее. 

Учитывая  направление  движения  взаимодействующих  волн  (спутные    и  встречные    по  отношению  к  исходному  потоку),  получаем  два  класса  задач  об  их  взаимодействии:  приходящие  волны  одного  ((или  )  или  различных  ()направлений.  Как  при  интерференции,  так  и  при  рефракции  волн  встречаются  оба  класса  задач.  Очевидно,  что  волны  разных  направлений  пересекаются  всегда,  а  возможность  взаимодействия  волн  одного  направления  нуждается  в  дополнительном  анализе.

Формула  интерференции  в  общем  виде  может  быть  записана  как

.  (7)

Например,  взаимодействие  догоняющих  скачков  уплотнения  (разывов  одного  направления)  можно  представить  в  виде

.  (8)

Тангенциальный  разрыв  разделяет  два  потока,  прошедших  через  разрывы  1  и  2  (догоняющие  приходящие  скачки  уплотнения)  и  отраженный  3.  Для  встречных  скачков  уплотнения  имеем

.  (9)

Все  возможные  в  обобщенной  УВС  формулы  взаимодействия  приведены  на  рис.  5  (ТК-1,2,3  —  тройные  конфигурации  ударных  волн).

Таблица  2.

2.3.Допустимые  перестройки  ударных  волн  и  волновых  фронтов

В  статье  И.А.  Богаевского  [14]  дана  классификация  перестроек  разрывов  в  потенциальных  решениях  уравнения  Бюргерса  и  в  вязких  решениях  уравнения  Гамильтона-Якоби  с  выпуклым  гамильтонианом.  Оказывается,  что  все  эти  классификации  одни  и  те  же.

Асимптотика  потенциальных  решений  ()  уравнения  Бюргерса    при  стремлении  вязкости    к  нулю  выражается  через  функцию  вида  F(λ)  =  min  f_λ(y),  где  λ  =  (t,  х)  —  точка  пространства-времени,  f  —  семейство  гладких  функций.  Хотя  семейство  f  —гладкое,  функция  F  имеет  особенности.  В  каждый  момент  времени  t  эти  особенности  представляют  собой  систему  ударных  волн  в  пространстве.  При  изменении  времени  t  система  ударных  волн  перестраивается.  В  качестве  t  может  выступать  и  любая  пространственная  координата. 

Нас  интересуют  только  особенности  и  перестройки,  устойчивые  относительно  любых  достаточно  малых  возмущений  гладких  начальных  условий.  Другие  особенности  и  перестройки  являются  структурно  неустойчивыми  и  на  практике  не  реализуются.  Оказывается,  что  в  типичные  моменты  времени  ударная  волна  общего  положения  имеет  особенности  из  конечного  списка  [13]  и  подвергается  перестройке  в  отдельные  моменты  времени.  Для  их  описания  рассмотрим  так  называемую  мировую  ударную  волну,  лежащую  в  пространстве-времени.  Мгновенные  ударные  волны  —  это  сечения  мировых  ударных  волн  изохронами  t  =  const.  Особенности  функций  минимума  семейств  общего  положения,  зависящих  от  небольшого  числа  параметров,  исследованы  в  [3]  и  [4].  На  существование  не­реализуемых  ударными  волнами  перестроек  функций  минимума  впервые  обра­тили  внимание  С.Н.  Гурбатов  [5]  и  А.И.  Саичев  [6].  Ю.М.  Барышников  показал  [1],  что  при  любых  начальных  условиях  гомотопические  типы  дополнений  мгновенной  ударной  волны  в  момент  перестройки  и  сразу  после  нее  совпадают.  Или,  что  тоже  самое,  в  некоторой  окрестности  точки  перестройки  в  простран­стве-времени  мгновенные  ударные  волны  в  близкие  моменты  времени,  непосред­ственно  следующие  за  перестройкой,  гомотопны  точке.

Рассмотрим  одномерный  случай  (размерность  d  =  1).  Мгновенная  ударная  волна  состоит  из  изолированных  точек,  а  мировая  ударная  волна  —  кривая  на  плоскости,  имеющая  регулярные,  тройные  и  концевые  точки  (рис.  5). 

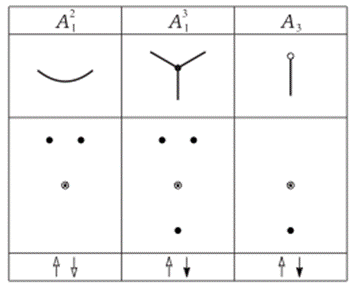
Рисунок  5.  Типичные  перестройки  ударных  волн  в  одномерном  ( d=1)  случае

В  первой  строке  введено  обозначение  особенности  мировой  ударной  волны.  Волна  может  зародиться  в  какой-то  момент  времени  (концевая  точка),  распространяться  в  пространстве  (регулярные  точки)  и  распадаться  с  образованием  трех  волн  (тройные  точки).  В  типичные  моменты  времени  мгновенная  ударная  волна  может  подвергаться  перестройкам,  изображенным  на  рис.  5  черными  стрелками.  А  именно,  любая  тройная  точка  мировой  ударной  волны  дает  пару  точек  мгновенной  ударной  волны  (изображены  во  второй  строчке),  а  концевая  точка  мировой  ударной  волны  порождает  новую  точку  мгновенной  ударной  волны.  Эти  две  перестройки  и  исчерпывают  все  типичные  перестройки  [14]. 

Рис.  6  иллюстрирует  плоский  случай  (d  =  2).  Мировая  ударная  волна  —  это  поверхность  с  особенностями;  все  эти  особенности  изображены  во  второй  строке.  Мгновенная  ударная  волна  —  это  кривая,  которая  может  иметь  тройные  и  концевые  точки  —  те  же  особенности,  которые  имеют  мировые  ударные  волны  в  случае  размерности  d  =  1.  Мгновенная  ударная  волна  может  подвергаться  перестройкам,  изображенным  на  рис.  6  черными  стрелками  [14].

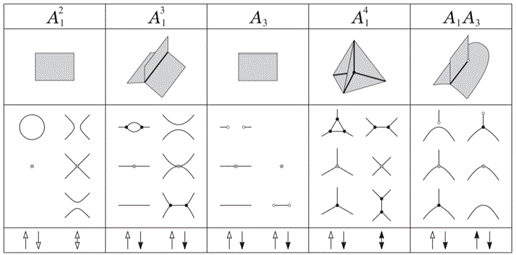
Рисунок  6.  Типичные  перестройки  ударных  волн  в  двумерном  ( d=2)  случае

Все  перестройки  волновых  фронтов  и  ударных  волн,  приведенные  на  рис.  5  и  6,  исчерпывают  возможные  виды  интерференции  одномерных  нестационарных  волн  и  двумерных  стационарных  и  нестационарных  волн  и  разрывов.  Аналогичным  образом  может  быть  введена  и  классификация  трехмерных  стационарных  и  нестационарных  волн.  В  этом  случае,  мировой  волной  будет  гиперповерхность  в  четырехмерном  пространстве-времени.  А  ее  сечениями  изохронами  t  будут  мгновенные  трехмерные  УВС.  Данный  случай  в  работе  не  рассматривается.

Заключение

Приведенная  здесь  классификация  является  наиболее  общей.  Она  содержит  в  себе  не  только  формулы,  следующие  из  обобщенной  УВС,  но  и  предсказывает  направление  возможных  взаимодействий  и  перестроек  волн.  Рассмотрены  различные  классификационные  признаки:  термодинамические,  кинематические,  нестационарность,  направление  разрыва,  приходящие  и  исходящие  разрывы,  обощенная  УВС,  конкретная  конфигурация  которой  определяется  параметрами  приходящих  разывов  и  УДС  на  исходящем  из  точки  интерференции  тангенциальном  разрыве.  С  другой  стороны,  выполнение  УДС  на  тангенциальном  разыве  за  УВС  является  необходимым,  но  не  достаточным  условием  существования  ударно-волновой  структуры.  Для  существования  УВС  должны  выполняться  условия  структурной  устойчивости,  изложенные  в  п.  2.2.  С  точки  зрения  размерности  время  является  всего  лишь  одной  из  координат,  т.  е.  кинематически  нестационарные  задачи  эквивалентны  стационарным  задачам  с  размерностью  на  единицу  больше.  Нужно  только  учитывать  тот  важный  факт,  что  четные  и  нечетные  размерности  описываются  разными  типами  геометрий  (симплектической  и  контактной),  соответственно,  и  классификации  задач  об  УВС  расслаиваются  на  два  множества:  четные  и  нечетные  пространство-время. 

Важно  —  кинематическая  эквивалентность  задач  не  означает  наличия  динамической  эквивалентности.  На  нестационарных  разрывах  происходит  изменение  полного  теплосодержания,  а  на  стационарных  скачках  уплотнения  (стоячих  волнах)  оно  остается  постоянным. 

Список  литературы:

1.Барышников  Ю.М.  Топология  перестроек  множеств  негладкости  функций  минимума  вариационных  задач//  Функц.  анал.  и  его  прил.  —  1990.  —  24,  №  3.  —  C.  62—63. 

2.Булат  П.В.,  Засухин  О.Н.,  Усков  В.Н.  (1993).  Формирование  струи  при  плавном  запуске  сопла  Лаваля.  ICH.:  течение  газа  в  каналах  и  струях.  Под  Ред.чл-  кор.  В.Г.  Дулова  СПБ.:  Издательство  СПбГУ,  —  С.  3—22.

3.Брызгалова  Л.Н.  Особенности  максимума  функции,  зависящей  от  параметров  //  Функцией,  анализ  и  его  прил.  —  1977.  —  Т.  11,  —  вып.  1.  —  С.  59—60.

4.Брызгалова  Л.Н.  Особенности  максимума  семейства  функций,  зависящих  от  параметров  //  Функцион.  анализ  и  его  прил.  —  1978.  —  Т.  12,  —  вып.  1.  —  С.  66—67.

5.Гурбатов  С.Н.,  Саичев  А.Н.  Вероятностные  распределения  и  спектры  потенциальной  гидродинамической  турбулентности  //  Изв.  вузов  //  Радиофизика.  —  1984.  —  Т.  27,  —  №  4.  —  С.  456—468.

6.Гурбатов  С.Н.,  Саичев  А.И.,  Шандарин  С.Ф.  Крупномасштабные  структуры  Вселенной  в  рамках  модельного  уравнения  нелинейной  диффузии.  Препринт  N"  152.  ИПМ  им.  Келдыша,  1984.

7.Кочин  Н.Е.,  Кибель  И.А.,  Розе  Н.В.  Теоретическая  гидромеханика,  ч.  II,  М.,  Физматгиз,  1963,  —  728  с.

8.Овсянников  Л.В.  Лекции  по  основам  газовой  динамики.  Москва-Ижевск:  Институт  компьютерных  исследований,  2003,  —  336  с.

9.Усков  В.Н.  и  др.  Интерференция  стационарных  газодинамических  разрывов.  Новосибирск:  ВО  «Наука»,  1995.  —  180  с.

10.Усков  В.Н.,  Чернышов  М.В.  (2006).  Дифференциальные  характеристики  поля  течения  плоской  перерасширенной  струи  в  окрестности  кромки  сопла.  Прикладная  Механика  И  Техническая  Физика,  Т.  47(№  3),  —  С.  72—83.

11.Усков  В.Н.  Бегущие  одномерные  волны.  СПб.:  БГТУ  «Военмех»,  2000.

12.Усков  В.Н.  (1979).  Интерференция  газодинамических  и  тангенциальных  разрывов.  Изв.  АН  СССР,  МЖГ.,  №  4,  —  С.  191.

13.Arnol’d  V.I.,  Baryshnikov  Yu.M.,  Bogaevsky  I.A.  Singularities  and  bifurcations  of  potential  flows//  Gurbatov  S.N.,  Malakhov  A.N.,  Saichev  A.I.  Nonlinear  random  waves  and  turbulence  in  nondispersive  media:  waves,  rays,  particles.  Manchester:  Manchester  Univ.  Press,  Manchester,  1991.  —  C.  290—300. 

14.Bogaevsky  I.A.  Perestroikas  of  shocks  and  singularities  of  minimum  functions//  Phys.  D.  2002.  —  173,  —  №  1—2.  —  С.  1—28. 

15.Uskov  V.N.,  Mostovykh  P.S.  Interference  of  Stationary  and  Non-Stationary  Shock  Waves  //  Shock  Waves.  —  2010.  —  Vol.  20  —  №  2,  —  P.  119—129.

16.Uskov  V.N.,  Mostovykh  P.S.  Differential  Characteristics  of  shock  wave  and  triple-shock-wave  configuration.  20th  International  Shock  Interaction  Symposium:  Book  of  Proceedings  (Stockholm,  Sweden,  20—24  August  2012)  KTH  Stockholm,  Sweden,  2012.  —  P.  211—214.

17.Uskov  V.N.,  Mostovykh  P.S..  Propagation  of  a  week  gasdynamic  gasconuity  in  a  steady  axisymmetric  flow.  //  19th  International  Shock  Interaction  Symposium:  Book  of  Proceedings  (Moscow-Russia,  August  31  —  September  3,  2010)  Moscow,  2010.  —  P.  4.