Статья опубликована в рамках: XXXI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 31 марта 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РЕГРЕССИОННО-НЕЧЕТКАЯ МОДЕЛЬ СЕРВЕРА
Афанасьева Татьяна Васильевна
д-р. техн. наук, профессор Ульяновского государственного технического университета, РФ, г. Ульяновск
E -mail: tv.afanasjeva@gmail.com
Козлов Александр Олегович
аспирант Ульяновского государственного технического университета, РФ, г. Ульяновск
REGRESSIVE-FUZZY MODEL OF SERVER
Afanasieva Tatiana
doctor of technical sciences, associate Professor, Ulyanovsk state technical university, Russia, Ulyanovsk
Kozlov Alexandr
postgraduate student of Ulyanovsk state technical university, Russia, Ulyanovsk
АННОТАЦИЯ
Назначение данной модели — прогнозирование состояния сервера по временным рядам физических числовых параметров и нечетким экспертным оценкам, включающих тенденции изменения нагрузки на сервер. Результаты применения модели показывают ее эффективность в плане повышения точности прогнозирования и информативности, полезные в приятии решений. Работа выполнена при поддержке РФФИ, проект № 14-07-00247.
ABSRACT
The purpose of this model — predict the state of the server on time series of physical parameters and fuzzy expert estimates, including trends in server load. The results of the model show its efficiency in improving the prediction accuracy and informational content, useful for decision making. This work was supported by RFBR project № 14-07-00247.
Ключевые слова : сервер; временные ряды; прогнозирование; нечеткая экспертная оценка; тенденция.
Keywords : server; time series; predict; fuzzy expert estimates; trend.
Задача изменения нагрузки на отдельный сервер, приводящей к потере его работоспособности является актуальной, так как ее неадекватное решение может привести к потере ценной информации и значительным материальным затратам. Следует учесть, что изменение нагрузки может возникнуть и в случае воздействия на сервер внешних факторов, а поэтому формулируемых экспертно, например, таких как увеличение объема решаемых задач, рост числа клиентов, изменение масштаба предприятия. Чтобы обеспечить раннее предупреждение о возможных в будущем нарушениях функционирования сервера и учесть эти риски при планировании развития ИТ-ресурсов предприятия целесообразно применять методы анализа временных рядов (ВР) физических параметров сервера, уточняя результаты на осснове внешних экспертных оценок тенденций развития предприятия.
Для решения обозначенной задачи предлагается обобщенная модель состояния сервера, интегрирующая математические модели временных рядов его числовых параметров в виде адаптивных динамических регрессий [1, c. 125], и нечеткие модели экспертного оценивания [2, c. 61].
В качестве числовых параметров сервера использованы ВР максимальных суточных значений числовых параметров сервера: «Загрузка центрального процессора», «Загрузка оперативной памяти», «Загрузка сети». В качестве внешней экспертной оценки выбран прогноз тенденции развития предприятия.
Модель поведения сервера, интегрирующая числовые параметры и экспертные оценки, представим в виде
|
|
( |
где: ![]() — метод, генерирующий комплексную прогнозную оценку состояния сервера;
— метод, генерирующий комплексную прогнозную оценку состояния сервера;
![]() — вектор ВР, характеризующих прогнозное техническое состояние сервера;
— вектор ВР, характеризующих прогнозное техническое состояние сервера;
![]()
где: ![]() — вектор внутренних экспертных оценок числовых параметров
— вектор внутренних экспертных оценок числовых параметров ![]() , например, «Недостаток загрузки», «Превышение загрузки», «Норма»;
, например, «Недостаток загрузки», «Превышение загрузки», «Норма»;
![]() — вектор экспертных оценок значений параметров
— вектор экспертных оценок значений параметров ![]() ;
;
![]() — вектор экспертных оценок тенденций изменения параметров («Рост», «Падение», «Стабильность»);
— вектор экспертных оценок тенденций изменения параметров («Рост», «Падение», «Стабильность»);
![]() — некоторый метод определения внутренних экспертных оценок числовых параметров
— некоторый метод определения внутренних экспертных оценок числовых параметров ![]() ;
;
![]() — экспертная оценка, характеризующая внешние факторы изменения предприятия и выражаемая в виде набора нечетких термов тенденций «Уменьшение нагрузки», «Стабильность», «Увеличение нагрузки»;
— экспертная оценка, характеризующая внешние факторы изменения предприятия и выражаемая в виде набора нечетких термов тенденций «Уменьшение нагрузки», «Стабильность», «Увеличение нагрузки»;
![]() — прогнозное состояние сервера, задаваемое нечетким термом из множества значений: «Недостаток загрузки», «Норма», «Превышение загрузки».
— прогнозное состояние сервера, задаваемое нечетким термом из множества значений: «Недостаток загрузки», «Норма», «Превышение загрузки».
Модель ВР числовых параметров
|
|
|
представим в виде зависимостей, отражающих особенности их поведения:
|
|
|
где: ![]() — неслучайная функция полиномиального тренда, имеющая вид:
— неслучайная функция полиномиального тренда, имеющая вид:
|
|
|
![]() — неслучайная периодическая функция:
— неслучайная периодическая функция:
|
|
|
![]() — случайная с элементами регулярности функция, которая может включать в себя процессы АРСС(p,q):
— случайная с элементами регулярности функция, которая может включать в себя процессы АРСС(p,q):
|
|
|
а также процесс GARCH(p,q):
|
|
|
![]() — нерегулярная случайная компонента.
— нерегулярная случайная компонента.
Тогда модель прогноза каждого числового параметра сервера
|
|
|
где: р — горизонт прогноза.
Модель экспертной оценки числового параметра сервера представим в виде функций принадлежности ![]() ,
, ![]() ,
, ![]() ,
, ![]() терм-множества
терм-множества ![]() {«Очень низкий», «Низкий», «Ниже среднего», «Среднее», «Выше среднего», «Высокий», «Очень высокий»}:
{«Очень низкий», «Низкий», «Ниже среднего», «Среднее», «Выше среднего», «Высокий», «Очень высокий»}:
|
|
|
где ![]() ,
, ![]() ,
, ![]()
Модель экспертной оценки прогнозной нечеткой тенденции ![]() изменения числового параметра определим в виде алгоритмически заданных операций ACL-шкалы [3, с. 92]
изменения числового параметра определим в виде алгоритмически заданных операций ACL-шкалы [3, с. 92]
|
|
|
где
|
|
|
|
|
|
|
|
|
Тогда модель прогноза отдельного параметра сервера:
|
|
(1) |
![]() — прогнозная лингвистическая оценка состояния отдельного параметра сервера;
— прогнозная лингвистическая оценка состояния отдельного параметра сервера;
![]() — правила определения состояния отдельного параметра сервера;
— правила определения состояния отдельного параметра сервера;
![]() — прогнозная лингвистическая оценка общей тенденции нечеткого временного ряда отдельного параметра сервера,
— прогнозная лингвистическая оценка общей тенденции нечеткого временного ряда отдельного параметра сервера, ![]() нечеткая оценка последнего спрогнозированного значения отдельного параметра сервера.
нечеткая оценка последнего спрогнозированного значения отдельного параметра сервера.
|
|
(2) |
Обобщенная нечеткая модель состояния сервера определим в виде
|
|
|
где: ![]() — итоговая прогнозная лингвистическая оценка состояния сервера;
— итоговая прогнозная лингвистическая оценка состояния сервера;
![]() — экспертная оценка, характеризующая внешние факторы изменения предприятия;
— экспертная оценка, характеризующая внешние факторы изменения предприятия;
![]() — прогнозная лингвистическая оценка состояния отдельных характеристик сервера, получаемая по формулам (1), (2);
— прогнозная лингвистическая оценка состояния отдельных характеристик сервера, получаемая по формулам (1), (2);
![]() — набор правил определения прогнозной оценки стояния сервера:
— набор правил определения прогнозной оценки стояния сервера:
|
|
(3) |
где: ![]() — лингвистический терм прогнозной оценки состояния отдельного параметра сервера,
— лингвистический терм прогнозной оценки состояния отдельного параметра сервера,
![]() — лингвистический терм прогнозной оценки тенденции развития предприятия.
— лингвистический терм прогнозной оценки тенденции развития предприятия.
Результаты применения предложенной регрессионно-нечеткой модели были проанализированы по критерию точности и информативности. По сравнению с традиционным визуальным методом анализа и прогнозирования состояния сервера, предложенный подход позволяет получать более информативные данные, необходимые для принятия решений: информационный объем сообщения о состоянии сервера, вычисленный по формуле Хартли, увеличился в 3 раза. Другим положительным эффектом является повышение точности прогнозирования ситуаций, приводящих к потере работоспособности сервера в 2,5 раз (с 7 ситуаций до 18 ситуаций).
Список литературы:
1.Валеев С.Г. Регрессионное моделирование при обработке наблюдений. М.: Наука, 1991. — 272 c.
2.Ярушкина Н.Г. Интегральный метод нечеткого моделирования и анализа нечетких тенденций / Н.Г. Ярушкина, Т.В. Афанасьева, И.Г. Перфильева // Автоматизация процессов управления. — № 2(20). — 2010. — С. 59—64.
3.Афанасьева Т.В. Модель ACL-шкалы для генерации лингвистических оценок в принятии решений / Т.В. Афанасьева // Вопросы современной науки и практики. Университет им. В.И. Вернадского. Т. 2. Серия «Технические науки». Тамбов, ТГТУ, — 2008. — № 4(14). — С. 91—97.
дипломов


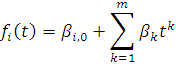
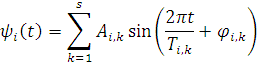
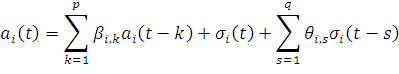
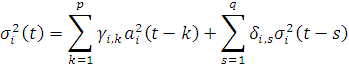
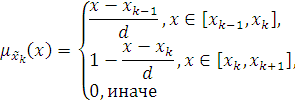
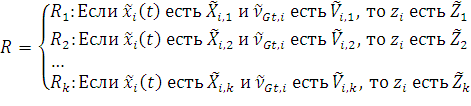
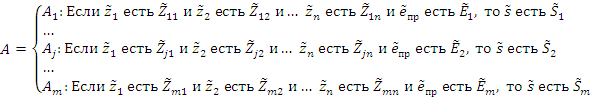
Оставить комментарий