Статья опубликована в рамках: XXVI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 05 ноября 2013 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ НАГРЕВА ПРИ ОБРАБОТКЕ МАТЕРИАЛОВ ДВИЖУЩИМСЯ ИНТЕНСИВНЫМ ИСТОЧНИКОМ ТЕПЛА
Прохоров Александр Владимирович
канд. техн. наук, доцент, филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет) в г. Озерске, г. Озерск Челябинской обл.
E-mail: Prokhorov@bk.ru
Омельченко Светлана Владимировна
канд. пед. наук, филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет) в г. Озерске, г. Озерск Челябинской обл.
MODELLING OF HEAT TREATMENT OF MATERIALS MOVING IN INTENSE HEAT SOURCE
Prokhorov Alexander
candidate of technical Sciences, Branch of Federal State State-Financed Educational Institution of Higher Professional Education «South Ural State University» (national research university) in Ozersk, Ozersk
Omelchenko Svetlana
candidate of pedagogical Sciences, Branch of Federal State State-Financed Educational Institution of Higher Professional Education «South Ural State University» (national research university) in Ozersk, Ozersk
АННОТАЦИЯ
В статье рассматриваются вопросы моделирования нестационарного режима нагрева толстой плиты интенсивным движущимся источником теплоты. Получено аналитическое распределение температурных полей в зависимости от времени и координат. Проведен расчет градиентов температур для бетонной и стальной плиты; определено минимальное число подогревающих горелок.
ABSTRACT
The article envisages the modelling of non-stationary heating mode of a thick plate moving in an intense heat source. Analytical distribution of temperature gradients in relation to time and position data is obtained. The calculation of temperature gradients for concrete and steel plates is carried out; minimal number of heating burners is estimated.
Ключевые слова: моделирование; теплопроводность; твердое тело; источник теплоты.
Keywords: modelling, thermal conductivity, a solid, a heat source.
В металлургии, машиностроении, легкой промышленности и медицине широко используются технологии, в которых обрабатываемый материал перемещается относительно источника тепла с определенной скоростью. Так, лазерным лучом и плазменной струей производится резка, сварка и термообработка различных материалов, с помощью горелок на жидком и газообразном топливе выполняется подогрев и зачистка листовой стали перед обработкой давлением и т. д.
Для контроля за тепловым состоянием обрабатываемого материала служат теплоизмерительные приборы, но в ряде случаев, когда применение измерительной техники затруднительно, используют расчетные методики.
В известных публикациях [1, 2, 5] расчет температуры проводится по формулам, полученным с помощью уравнения Пуассона для мгновенных источников теплоты или функции Грина. При этом многие расчетные выражения содержат неберущиеся интегралы или не учитывают важные условия протекания процесса (например, теплообмен с окружающей средой, конечную толщину изделия и т. п.).
В настоящей работе задача о стационарном поле в толстой плите решается в координатах, связанных с быстроперемещающимся источником. Исходное дифференциальное уравнение и граничные условия имеют вид:
|
|
(1) |
|
|
(2) |
В этих выражениях ![]() — приращение температуры; — скорость движения источника;
— приращение температуры; — скорость движения источника; ![]() , ,
, , ![]() — координаты;
— координаты; ![]() — коэффициент температуропроводности;
— коэффициент температуропроводности; ![]() — приведенный коэффициент теплоотдачи; — полуширина плиты;
— приведенный коэффициент теплоотдачи; — полуширина плиты; ![]() — толщина плиты, — функция внутренних источников, моделирующих действие кругового нормально распределенного источника теплоты;
— толщина плиты, — функция внутренних источников, моделирующих действие кругового нормально распределенного источника теплоты; ![]() — оператор Лапласа, в котором отсутствует
— оператор Лапласа, в котором отсутствует ![]() из-за малости в сравнении с
из-за малости в сравнении с ![]() . Для удобства расчетов и последующего анализа функция взята в форме [3, 4]
. Для удобства расчетов и последующего анализа функция взята в форме [3, 4]
|
|
(3) |
где: ![]() — плотность тепловыделения при
— плотность тепловыделения при ![]() ;
;
![]() ,
, ![]() — теплоемкость и плотность материала;
— теплоемкость и плотность материала;
![]() — характерный размер источника (луча, факела и т. д.);
— характерный размер источника (луча, факела и т. д.);
![]() — большое положительное число (как показал анализ,
— большое положительное число (как показал анализ, ![]() 5000).
5000).
Решение (1)—(3) методом Фурье дает выражение для определения температурного поля в плите:
|
|
(4) |
Здесь 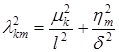 ;
; ![]() ;
; ![]() — корни характеристического уравнения
— корни характеристического уравнения ![]() , полученного из граничных условий (2);
, полученного из граничных условий (2); ![]() — интеграл ошибок; связана с плотностью тепловыделения
— интеграл ошибок; связана с плотностью тепловыделения ![]() зависимостью
зависимостью ![]() .
.
Расчет распределения температуры в плите по (4) был выполнен для двух случаев:
а) бетонная плита — =840 Дж/(кг×К), =2000 кг/м3, =7,6×10-7 м2/с, =0,05 м, =0,3 м, =1 м, =0 и =200 м-1, =0,3 м/с, =5×104 Вт;
б) стальная плита — =460 Дж/(кг×К), =7800 кг/м3, =1,25×10-5 м2/с, =0,05 м, =0,1 м, =1 м, =1 м-1, =0,1 м/с, =15×104 Вт;
Результаты расчета показали, что максимум температуры резко падает с увеличением , а положение максимума быстро смещается по оси (=0, для бетона при =0 =2014 °С, =0,033 м; при =0,5 мм =1000 °С, =0,087 м, при =1 мм =600 °С, =0,21 м).
Теплоотвод с поверхности (=0) бетонной плиты (=200 м-1) уменьшает величину температуры до =1837 °С, а при больших заметно ее переохлаждает по сравнению с глубинными слоями (=6 м, при =0 Т=48 °С, при =1 мм Т=57 °С).
Высокие теплопроводность и плотность стали требуют увеличения тепловой мощности горелки и снижения скорости движения для достижения высоких температур (=0, =1203 °С при =0,1 м/с и =15×104 Вт).
Распределение температуры по оси позволяет найти число горелок для организации равномерного нагрева по ширине стального листа (для =1 м требуется 10 горелок с данным распределением плотности теплового потока ![]() в факеле).
в факеле).
Список литературы:
1.Обеснюк В.Ф. Нагрев конструкции движущимся плазменным источником / В.Ф. Обеснюк, Н.В. Пашацкий, С.В. Осовец // Инженерно-физический журнал. — 1999. — Т. 72, — № 2. — С. 232—235.
2.Осовец С.В. Расчет нестационарного теплового состояния плиты при ее нагреве перемещающимся источником / С.В. Осовец, Е.В. Торопов, А.В. Прохоров, В.Л. Кириллов // Инженерно-физический журнал. — 2000. — Т. 73, — № 4. — С. 757—760.
3.Пашацкий Н.В. Тепловые процессы при обработке предварительно нагретой стальной плиты огневой машиной / Н.В. Пашацкий, А.В. Прохоров // Известия ВУЗов. Черная металлургия. — 2001. — № 3. — С. 46—48.
4.Прохоров А.В. Моделирование движущихся приповерхностных источников тепла / А.В. Прохоров // Инновации в науке. — 2013. — № 16-1. — С. 16—20.
5.Рыкалин Н.Н. Расчеты тепловых процессов при сварке / Н.Н. Рыкалин. М.: Машгиз, 1951.
дипломов


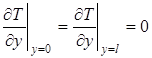 ,
,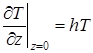 ,
,  .
.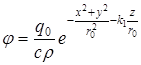 ,
,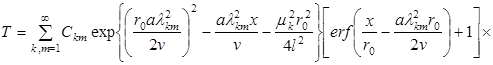
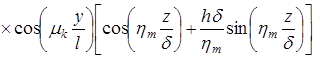 ,
,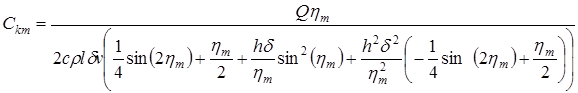
Оставить комментарий