МЕТОД  МОНТЕ-КАРЛО  ДЛЯ  РЕШЕНИЯ  ЗАДАЧ  ФУНКЦИОНАЛЬНОЙ  ВЗАИМОЗАМЕНЯЕМОСТИ

Колчков  Вячеслав  Иванович

канд.  техн.  наук,  профессор  Московского  государственного  машиностроительного  университета  (МАМИ),  г.  Москва

E-mail: 

METHOD  MONTE-KARLO  FOR  THE  DECISION  OF  PROBLEMS  FUNCTIONAL  INTERCHANGEABILITY

Vyacheslav  Kolchkov

candidate  of  Technical  Sciences,  Professor  of  MSMU,  Moscow

АННОТАЦИЯ

Рассмотрено  применение  метода  Монте-Карло  как  численного  метода  решения  статистических  задач  при  обеспечении  функциональной  взаимозаменяемости.  Физический  эксперимент  заменён  математическим  исследованием  при  сохранении  сущности  и  характера  эксперимента.

ABSTRACT

The  application  of  the  Monte  Carlo  method  as  a  numerical  method  for  solving  statistical  problems  in  ensuring  the  functional  interchangeability.  Physical  Experiment  replaced  mathematical  research  while  maintaining  the  essence  and  nature  of  the  experiment. 

Ключевые  слова:  функциональная  взаимозаменяемость;  геометрические  характеристики;  размерные  характеристики;  точность  параметра;  погрешность  размера;  допуск;  метод  статистических  испытаний;  метод  Монте-Карло.

Keywords:  functional  interchangeability;  geometric  characteristics;  size  characteristics;  the  accuracy  of  the  parameter;  uncertainty  size;  tolerance,  the  method  of  statistical  tests;  the  Monte  Carlo  method.

Обеспечение  функциональной  взаимозаменяемости  изделий  предусматривает  расчёты  и  оптимизацию  параметров  точности:  допусков  и  предельных  отклонений  размеров,  допусков  формы  и  расположения  поверхностей,  а  также  параметров  шероховатости  поверхностей.  Эти  расчёты  основаны  на  установлении  взаимосвязей  показателей  качества  изделия  с  функциональными  параметрами  его  деталей  и  сборочных  единиц  [4,  с.  224]. 

Назначение  оптимальных  точностных  требований  к  функциональным  параметрам  позволяет  создать  гарантированный  запас  работоспособности  изделий  при  обеспечении  в  заданных  пределах  их  эксплуатационных  показателей.  Они  определяют  качество  функционирования,  например:  надёжность,  производительность,  точность  и  т.  п.  Изготовление  деталей  и  сборочных  единиц  изделия  с  установленной  точностью  по  геометрическим,  механическим,  электрическим  и  другим  функциональным  параметрам  обеспечивает  функциональную  взаимозаменяемость  всех  однотипных  изделий,  выпускаемых  предприятием. 

При  проектировании  изделий  и  назначении  допусков  на  геометрические  характеристики  деталей  необходимо  учитывать  действительное  состояние  параметров  на  различных  этапах  жизненного  цикла:  изготовление,  эксплуатация  и  ремонт  [2].  Такой  методологический  подход  к  проектированию  позволит  сократить  расходы  на  длительную  доводку  нового  изделия  на  экспериментальных  стендах,  т.  е.  обеспечить  необходимые  показатели  назначения  и  их  стабильность  во  времени  для  партии  однородной  продукции  непосредственно  после  изготовления  и,  следовательно,  повысить  конкурентоспособность.  При  фиксированном  конструктивном  исполнении  изделия  заданное  качество  совокупности,  т.  е.  всех  однотипных  изделий,  будет  обеспечиваться  точностью  функциональных  параметров  его  составных  частей,  причем  под  точностью  понимается  степень  приближения  значения  параметра  к  заданному  при  проектировании,  с  учетом  состояния  изделия  при  различных  эксплуатационных  режимах,  а  также  изменения  его  во  времени. 

Следует  также  иметь  в  виду,  что  функциональные  геометрические  параметры  в  машине  или  другом  изделии  взаимозависимы  и  связаны  с  геометрическими  параметрами  всех  деталей,  входящих  в  размерные  и  кинематические  цепи.  Изменение  размера  одной  детали  узла  или  механизма  влечет  за  собой  изменение  размера  или  взаимного  расположения  осей  и  поверхностей  одной  или  нескольких  деталей. 

Главная  цель  функциональной  взаимозаменяемости  не  может  быть  достигнута,  если  не  установлены  взаимосвязи  основных  функциональных  параметров  и  показателей  качества  машины.  Установление  этих  зависимостей  базируется  на  фундаментальных  знаниях  в  той  области  науки  и  техники,  которые  описывают  принцип  функционирования  изделий  данного  типа.  Кроме  того,  конкретные  машины  имеют  свои  конструктивные  и  технологические  особенности,  требующие  внесения  определенных  уточнений  и  поправок  в  теоретические  зависимости.  Эти  поправки,  как  правило,  сводятся  к  введению  в  соответствующие  формулы  эмпирических  коэффициентов,  с  целью  приближения  к  описанию  реальных  процессов  функционирования  машины.  В  случае  стохастических,  вероятностных  связей  —  для  получения  конкретных  решений  при  проектировании  изделий,  требуется  установление  или  уточнение  действительных  законов  распределения  функциональных  параметров. 

Наряду  с  установлением  функциональных  зависимостей,  важнейшим  вопросом  исследования  взаимосвязи  точности  функциональных  параметров  и  эксплуатационных  показателей  является  выбор  методов  анализа  и  синтеза  точности.  Применительно  к  производству  изделий  машиностроения  можно  выделить  следующие  методы  расчета  точности:  а)  метод  граничных  испытаний;  б)  метод  натурных  испытаний;  в)  метод  определения  предельных  погрешностей  (по  максимуму-минимуму  или  теоретико-вероятностным  способом);  г)  метод  статистических  испытаний  математической  модели  (метод  Монте-Карло).

Метод  граничных  испытаний  позволяет  определить  диапазон  рассеяния  эксплуатационного  показателя  при  одновременном  изменении  только  двух  функциональных  параметров  и,  следовательно,  не  учитывает  одновременного  влияния  погрешностей  всех  функциональных  параметров.  Указанный  факт  является  существенным  недостатком  метода  граничных  испытаний.

Метод  натурных  испытаний  —  эмпирический  метод  оценки  точности  эксплуатационных  показателей.  Проводя  испытания  модели  или  натурного  образца  при  различных  погрешностях  функциональных  параметров,  а  затем  статистическую  обработку  результатов  испытаний  можно  получить  диапазон  рассеяния  эксплуатационного  показателя,  а  также  вероятность  попадания  его  в  заданное  поле  допуска.  Однако,  метод  натурных  испытаний  требует  больших  затрат  времени  и  средств  на  проведение  экспериментальных  работ  и  поэтому  имеет  ограниченное  применение.

Метод  определения  предельных  погрешностей  позволяет  при  известной  функциональной  связи  найти  предельные  отклонения  эксплуатационного  показателя.  Пусть  Y  —  эксплуатационный  показатель,  а  x₁  ,  x₂  ….  x_n  —  функциональные  параметры,  связь  между  которыми  выражена  зависимостью: 

Y  =  F  (x₁,  x₂,  x₃,  …,  x_n)  или  Y  +  ∆Y  =  F  (x₁  +  ∆x₁,  x₂  +  ∆x₂,  x₃  +  ∆x₃,  …,  x_n  +  ∆x_n),  где  ∆x_i  –  погрешности  функциональных  параметров. 

Разлагая  функцию  F(x)  в  ряд  Тейлора  и  пренебрегая  членами  2-го  порядка  малости,  имеем:

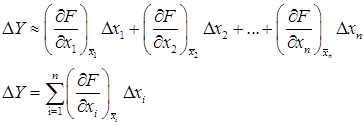
Погрешности  ∆x_i  могут  суммироваться  арифметически  (способ  максимума-минимума)  или,  учитывая,  что  они  являются  случайными  величинами,  квадратично  (вероятностный  способ).  Метод  определения  предельных  погрешностей  достаточно  широко  используется  для  решения  задач  обеспечения  функциональной  взаимозаменяемости  машин,  однако  существует  ряд  недостатков,  которые  ограничивают  его  применение.  К  ним  относятся:  а)  метод  применим  только  для  линейных  систем;  б)  априорное  нормальное  распределение  величин  функциональных  параметров  должно  соответствовать  апостериорному;  в)  метод  не  дает  количественной  оценки  вероятности  попадания  эксплуатационного  показателя  в  заданное  поле  допуска;  г)  погрешность  параметра  должна  быть  всегда  значительно  меньше  его  величины.

При  исследовании  функциональной  взаимозаменяемости  энергетических  машин,  например  поршневых  компрессоров,  зависимости  между  эксплуатационными  показателями  и  функциональными  параметрами  в  общем  случае  носят  нелинейный  характер,  а  распределение  функциональных  параметров  отличается  от  нормального.  Кроме  того,  эксплуатационные  показатели  компрессоров  зависят  от  таких  функциональных  параметров,  величины  погрешностей  которых  сравнимы  с  номинальными  значениями  параметров.  К  числу  указанных  функциональных  параметров  относятся  зазоры  в  сопряжениях  поршень-цилиндр,  линейное  мертвое  пространство  и  др.

Из  вышесказанного  видно,  что  для  анализа  взаимосвязей  точности  функциональных  параметров  с  эксплуатационными  показателями  энергетических  машин  необходимо  применять  более  совершенные  методы.  К  числу  таких  методов  относится  метод  статистических  испытаний  математических  моделей  (Монте-Карло)  [1],  который  лишен  недостатков,  присущих  вышеперечисленным  методам.  Исследование  основной  задачи  функциональной  взаимозаменяемости  методом  Монте-Карло  позволяет  установить  оптимальные  соотношения  между  погрешностями  функциональных  параметров  и  эксплуатационными  показателями,  а  также  дать  качественную  и  количественную  оценку  вероятности  попадания  эксплуатационного  показателя  в  заданное  поле  допуска.  При  этом  функциональные  связи  могут  быть  нелинейными,  а  распределение  функциональных  параметров  может  отличаться  от  нормального  закона.

Рассмотрим  задачу  анализа  и  синтеза  требований  к  точности  функциональных  параметров  ответственных  деталей  и  узлов  методом  Монте-Карло  на  примере  поршневых  компрессоров  высокого  давления,  имеющих  достаточно  сложные  размерные  и  кинематические  связи  и  высокие  требования  к  точности  поршневых  уплотнений  [5,  с.  116].

Функциональная  связь  величины  производительности  с  геометрическими  параметрами  деталей  и  узлов  компрессора,  а  также  с  параметрами  процесса  сжатия  может  быть  выражена  уравнением  (1),  являющимся  математическим  описанием  работы  компрессора  [5,  с.  135]. 

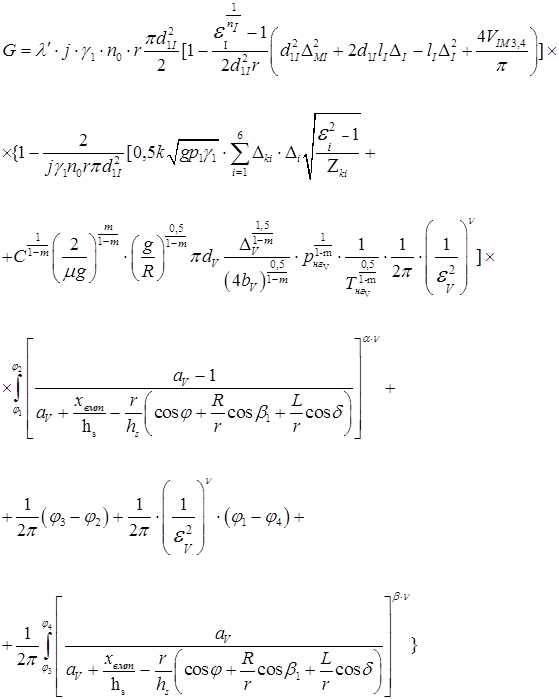(1)

Оно  включает  термодинамические  параметры  цикла,  кинематические  параметры  и  геометрические  параметры  его  деталей  и  соединений.  К  геометрическим  параметрам  относятся,  например:  зазоры  ∆_V,  ∆_I  в  поршневых  уплотнениях  5-ой  и  1-ой  ступеней;  линейные  мёртвые  пространства  ∆_MV,  ∆_MI  и  др.  Это  описание  в  сочетании  с  целевой  функцией  и  ограничениями  может  быть  принято  в  качестве  математической  модели  оптимизации  точности  функциональных  параметров.  Функцией  цели  является  достижение  установленного  уровня  производительности  (коэффициента  подачи)  и  обеспечение  его  в  заданных  пределах  для  всех  производимых  машин,  а  ограничениями  являются  экономические  показатели. 

Отклонение  величины  производительности  G  определяется  отклонениями  параметров,  входящих  в  уравнение  от  их  номинальных  значений.  Полагая,  что  отклонения  этих  параметров  являются  случайными  величинами,  можно  характеризовать  величину  G  математическим  ожиданием  m(G)  и  дисперсией  D(G).  Для  исследования  точностных  связей  необходимо  рассчитать  величину  производительности  G  при  различных  случайных  значениях  функциональных  параметров  ∆_V,  ∆_MV,  ∆_I,  ∆_MI,  ∆_KI,  ∆_KII,  r,  d_1I,  h_s,  b_V  и  др.  Значения  функциональных  параметров  должны  быть  взяты  из  генеральных  совокупностей  их  значений.  Математическое  ожидание  каждого  функционального  параметра  определяется  с  учетом  действия  температурных  и  силовых  деформаций.  При  этом  предполагается,  что  действие  температурных  и  силовых  деформаций  не  изменяет  диапазона  рассеяния  функционального  параметра,  но  смещает  координату  середины  поля  допуска,  т.  е.:

mA_i  =  A_i  +  ∆_oi  +  ∆_oit  +  ∆_oip,  где  mA_i  —  математическое  ожидание  i-го  функционального  параметра;  A_i  —  номинальное  значение  функционального  параметра;  ∆_oi  —  координата  середины  поля  допуска;  ∆_oit  —  смещение  координаты  середины  поля  допуска  из-за  температурных  деформаций;  ∆_oip  —  смещение  координаты  середины  поля  допуска  из-за  силовых  деформаций.

Закон  распределения  каждого  функционального  параметра  определяется  либо  априори,  либо  на  основании  статистической  обработки  данных  о  фактической  точности  изготовления  деталей  компрессора.

Алгоритм  взаимосвязи  производительности  компрессора  с  функциональными  параметрами,  выраженный  уравнением  (1),  программируется  для  расчета  на  компьютере  так,  чтобы  функциональные  параметры  могли  принимать  в  процессе  расчета  любые  случайные  значения.  Случайные  величины  вырабатываются  по  специальным  программам  или  с  помощью  генераторов  случайных  величин  см.  например  [3].  При  этом  закон  их  распределения  выбирается  идентичным  закону  распределения  соответствующего  функционального  параметра  компрессора.

Составленная  по  описанной  методике  математическая  модель,  полностью  отражает  взаимосвязь  точности  величины  производительности  с  функциональными  параметрами  деталей  и  узлов  компрессора  и  позволяет  имитировать  на  компьютере  дорогостоящие  и  трудоемкие  натурные  испытания.

Расчет  (испытание  модели)  дает  случайное  значение  производительности  G.  Многократное  повторение  расчетов  дает  совокупность  значений  величин  производительности,  которые  могут  встретиться  при  самых  различных  сочетаниях  случайных  величин  функциональных  параметров,  имеющих  место  при  серийном  изготовлении  компрессоров.

На  основе  математического  моделирования  с  помощью  метода  Монте-Карло  могут  быть  решены  как  задачи  анализа  точности  величины  производительности  компрессора,  так  и  задачи  синтеза  точности  функциональных  параметров  его  деталей  и  узлов.  В  первом  случае  по  распределениям  функциональных  параметров  с  заданными  математическими  ожиданиями  mA_i  и  дисперсиями  DA_i  необходимо  определить  распределение  величины  производительности  G,  т.  е.  значения  математического  ожидания  m(G)  и  дисперсии  D(G).

Метод  Монте-Карло  —  численный  метод  решения  статистических  задач  с  помощью  математического  моделирования  случайных  событий  или  процессов.  Он  заменяет  физический  эксперимент  математическим  исследованием,  сохраняя  сущность  и  характер  эксперимента.  Реализация  метода  статистических  испытаний  возможна  на  основе  программного  обеспечения  типа  Math  Cad  и  Excel.

Экономическая  целесообразность  состоит  в  том,  что  бы  на  этапе  проектирования  машин,  агрегатов  и  аппаратов  назначать  требования  к  точности  функциональных  параметров,  соответствующие  оптимальному  состоянию.  В  этом  случае  значительно  сокращаются  сроки  доводки  при  постановке  продукции  на  производство,  упрощаются  режимы  обкатки  и  уменьшается  время  выхода  на  нормальные  условия  эксплуатации.

Список  литературы:

1.Бусленко  Н.П.,  Шрейдер  Ю.А.  Метод  статистических  испытаний  (Монте-Карло)  и  его  реализация  на  цифровых  вычислительных  машинах.  М.:  Государственное  издательство  физ-мат.  литературы,  1961.  —  229  с.

2.Колчков  В.И.  Инверсия  точности  размерных  параметров  деталей  на  этапах  жизненного  цикла  изделия  //  Технические  науки  —  от  теории  к  практике.  —  2012.  —  16.  —  С.  7—13  /  НЭБ.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://elibrary.ru/download/78279702.pdf 

3.Колчков  В.И.  //  Консультационно-информационный  ресурс  «Точность-Качество».  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.micromake.ru/old/msis/zadankrmsis/slcifri.htm 

4.Колчков  В.И.  Метрология,  стандартизация  и  сертификация:  Учебник  для  ВУЗов.  М.:  Форум,  2013.  —  432  с.

5.НикифоровА.  Д.,  Колчков  В.И.,  Поликарпов  М.И.  Обеспечение  качества  нефтехимического  оборудования.  М.:  Машиностроение,  1984.  —  174  с.