Статья опубликована в рамках: XXVI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 05 ноября 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНОГО НАГРЕВА ЗАГОТОВКИ ПРИ ПЛАЗМЕННО–МЕХАНИЧЕСКОЙ ОБРАБОТКЕ
Прохоров Александр Владимирович
канд. техн. наук, доцент, филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет) в г. Озерске, г. Озерск Челябинской обл.
E-mail: Prokhorov@bk.ru
Омельченко Светлана Владимировна
канд. пед. наук, филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет) в г. Озерске, г. Озерск Челябинской обл.
MODELING THE NONSTATIONARY MODE OF BILLET HEATING AT PLASMA-MECHANICAL PROCESSING
Prokhorov Alexander
candidate of technical Sciences, Branch of Federal State State-Financed Educational Institution of Higher Professional Education «South Ural State University» (national research university) in Ozersk, Ozersk
Omelchenko Svetlana
candidate of pedagogical Sciences, Branch of Federal State State-Financed Educational Institution of Higher Professional Education «South Ural State University» (national research university) in Ozersk, Ozersk
АННОТАЦИЯ
В статье рассматриваются вопросы моделирования нестационарного режима резания заготовок при плазменно-механической обработке. Получено аналитическое распределение температурных полей в безразмерном варианте. Указаны границы практического использования влияния нестационарности процесса нагрева.
ABSTRACT
The article considers the questions of modelling the nonstationary mode at plasma-mechanical processing. The analytical distribution of temperature gradients in dimensionless form is obtained. The boundaries of the practical application of nonstationary heating process effect.
Ключевые слова: моделирование; теплопроводность; твердое тело; источник теплоты.
Keywords: modelling, thermal conductivity, a solid, a heat source.
Применение способа плазменно–механической обработки (ПМО) позволяет значительно увеличить производительность процесса резания труднообрабатываемых сталей и сплавов за счет разупрочнения срезаемого слоя плазменной дугой [2, 4]. Знание распределения температуры в обрабатываемой заготовке позволяет судить о структурных превращениях в материале и изменениях его механических характеристик [1, 5, 6].
При разработке аналитического метода расчета предполагается, что источник тепла (опорное пятно дуги) является быстроперемещающимся в направлении окружной скорости, температура по окружности мало изменяется, и пятно нагрева эквивалентно по действию кольцевому источнику.
Стационарный режим ПМО подробно рассмотрен в [3]. Исследуем нестационарный режим. Запишем дифференциальное уравнение теплопроводности для движущейся в осевом направлении цилиндрической заготовки в следующем виде:
|
|
(1) |
где: ![]() — безразмерная температура;
— безразмерная температура;
![]() — абсолютная температура;
— абсолютная температура;
![]() — предельная температура эксплуатации инструмента;
— предельная температура эксплуатации инструмента;
![]() — начальная температура;
— начальная температура;
![]() ,
, ![]() — безразмерные координаты;
— безразмерные координаты;
![]() — критерий Фурье;
— критерий Фурье;
![]() , — цилиндрические координаты, связанные с источником;
, — цилиндрические координаты, связанные с источником;
![]() — время;
— время;
— функция внутренних источников тепла;
— радиус заготовки.
Для решения задачи функцию внутренних источников тепла , моделирующую действие плазменной дуги на заготовку, представим в виде:
|
|
(2) |
Здесь ![]() — плотность тепловыделения внутренних источников в точке с координатами = 0 и
— плотность тепловыделения внутренних источников в точке с координатами = 0 и ![]() = 1; — радиус заготовки;
= 1; — радиус заготовки; ![]() — коэффициент теплопроводности;
— коэффициент теплопроводности; ![]() – коэффициент температуропроводности;
– коэффициент температуропроводности; ![]() ,
, ![]() — теплоемкость и плотность материала.
— теплоемкость и плотность материала.
Граничные условия принимаются следующими:
|
|
(3) |
где: ![]() — критерий Био;
— критерий Био;
![]() — коэффициент теплоотдачи.
— коэффициент теплоотдачи.
После решения уравнения (1) с учетом (2) и (3) и нулевого начального условия методом Фурье было получено выражение для расчета нестационарных температурных полей в цилиндрической заготовке:
|
(4) |
Для оценки влияния нестационарности на температурные поля в цилиндрическом теле были проведены расчеты по (4) и по формулам, полученным в [3]. Результаты расчетов показали, что нестационарность процесса следует учитывать при обработке участков длиной ![]() . Так как при плазменно-механической обработке [5], как правило, нагреву подвергаются участки длиной > 1, то в этом случае нестационарностью процесса можно пренебречь и для расчетов использовать соотношение [3]:
. Так как при плазменно-механической обработке [5], как правило, нагреву подвергаются участки длиной > 1, то в этом случае нестационарностью процесса можно пренебречь и для расчетов использовать соотношение [3]:


 .
.
Выводы
1. Рассмотрена нестационарная задача с движущимся источником тепла (плазменно–механическая обработка цилиндрических тел), в которой для моделирования действия плазменной дуги на заготовку использован метод внутренних источников.
2. Выявлено, что при плазменно–механической обработке участков длиной > 0,5 ( > 0,5 можно не учитывать нестационарность процесса и использовать в инженерных расчетах более простое соотношение для стационарного случая из [3].
Список литературы:
1.Осовец С.В. Расчет нестационарного теплового состояния плиты при ее нагреве перемещающимся источником / С.В. Осовец, Е.В. Торопов, А.В. Прохоров, В.Л. Кириллов // Инженерно-физический журнал. — 2000. — Т. 73, — № 4. — С. 757—760.
2.Пашацкий Н.В. Тепловые процессы при обработке предварительно нагретой стальной плиты огневой машиной / Н.В. Пашацкий, А.В. Прохоров // Известия ВУЗов. Черная металлургия. — 2001. — № 3. — С. 46—48.
3.Пашацкий Н.В. Аналитическая модель нагрева заготовки при плазменно-механической обработке / Н.В Пашацкий, А.В. Прохоров // Технология машиностроения. — 2002. — № 1. — С. 8—9.
4.Прохоров А.В. Теплопроводность и массообмен в системах с приповерхностными источниками: дис. … канд. техн. наук / А.В. Прохоров. Озерск, 2003. — 122 с.
5.Строшков А.Н. Обработка резанием труднообрабатываемых материалов с нагревом / А.Н. Строшков. М.: Машиностроение, 1977.
6.Шатерин М.А. Эффективность нагрева заготовки при плазменно-механической обработке / М.А. Шатерин, А.Л. Попилов, В.С. Медко // Сварочное производство. — 1982. — № 5. — С. 29—30.
дипломов


 ,
, .
. ;
;  ;
; 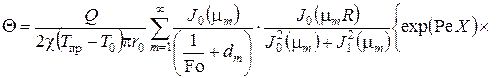


 ,
,
Оставить комментарий