К  ВОПРОСУ  ПОИСКА  АНОМАЛИЙ  ВО  ВРЕМЕННЫХ  РЯДАХ

Заварзин  Денис  Валерьевич

аспирант  кафедры  информационных  систем,  Ульяновский  государственный  технический  университет,  РФ,  г.  Ульяновск

E-mail: 

ABOUT  ANOMALIES  DETECTION  TECHNIQUES  IN  TIME  SERIES

Zavarzin  Denis

graduate  Student  of  Information  Systems  department,  Ulyanovsk  State  Technical  University,  Russia  Ulyanovsk

АННОТАЦИЯ

В  данной  работе  рассмотрена  актуальность  проблемы  обнаружения  аномалий  в  одномерных  числовых  и  нечетких  временных  рядах,  приведена  классификация  задач  и  методов,  при  помощи  которых  ведется  поиск  аномалий,  а  также  сферы  человеческой  жизнедеятельности,  где  эта  область  исследования  актуальна  в  настоящее  время.

ABSTRACT

In  this  paper  we  consider  the  importance  of  the  problem  of  anomaly  detection  in  one-dimensional  numerical  and  fuzzy  time  series,  shows  the  classification  of  anomaly  detection  problems  and  anomaly  detection  techniques  as  well  as  the  sphere  of  human  activity,  where  this  field  of  research  is  relevant  today.

Ключевые  слова:  аномалии;  временной  ряд;  нечеткая  тенденция;  обнаружение  аномалий;  методы  поиска  аномалий.

Keywords:  anomaly,  time  series;  fuzzy  trend;  anomaly  detection;  anomaly  detection  techniques.

Аномалии  представляют  собой  некоторые  паттерны  на  временном  ряду  (ВР),  для  которых  характерно  поведение,  неудовлетворяющих  предполагаемому  типовому  поведению.  Задача  же  поиска  и  выделения  аномалии  во  временном  ряду  характеризуется  понятием  «обнаружение  аномалии»  [5,  c.  1].

Проблема  обнаружения  аномалий  на  некотором  множестве  дискретных  данных,  характеризующих  единый  процесс,  является  актуальной  и  активно  изучается.  В  частности  был  выделен  целый  ряд  областей  человеческой  жизнедеятельности,  где  решение  задачи  поиска  аномалий  может  привести  к  качественному  улучшению  получаемых  результатов:

1.  Безопасность  и  защита  информации  (выявление  мошеннических  действий  в  банковской  сфере,  мобильной  связи,  обнаружение  угроз  в  компьютерных  сетях  и  т.  д.)  [4,  с.  12].

2.  Медицина  и  социальная  сфера  (диагностика  заболеваний,  социальная  статистика,  эконометрика,  мониторинг  в  ЖКХ)  [4,  с.  16].

3.  Промышленность  (мониторинг  неисправностей  механизмов,  рассогласование  технологических  процессов  и  т.  д.)  [4,  с.  17].

4.  Обработка  и  распознавание  изображений,  текста,  человеческой  речи  [4,  с.  18].

5.  Другие  сферы  деятельности  (например,  глобальный  экологический  мониторинг,  робототехника,  телекоммуникации).

Практически  любые  наблюдения,  полученные  в  результате  мониторинга  процессов  из  приведенных  выше  сфер  деятельности,  могут  быть  представлены  в  виде  числовой  последовательности  зависимой  от  времени,  т.  е.  в  форме  ВР  (например,  динамика  изменения  температуры  по  месяцам,  где  явно  обозначена  аномально  низкое  падение  температуры  в  июне)  (рис.  1). 

Таким  образом,  задача  обнаружения  аномалий  включается  в  задачу  анализа  ВР,  его  интерпретации  и  диагностики.  Целью  анализа  временного  ряда  является  достижение  понимания  причинных  механизмов,  обусловивших  поведение  изучаемого  процесса,  построение  моделей  временных  рядов,  которые  не  только  объясняют  поведение  процесса,  но  и  могут  быть  использованы  для  оценки  прогноза  развития  изучаемого  процесса  [3,  c.  46]. 

Например,  в  сфере  медицины  выявление  у  пациента  аномальной  тенденции  на  ВР  электроэнцефалограммы  может  служить  основанием  для  постановки  диагноза  и  краткосрочном  прогнозировании  течения  заболевания  сердечнососудистой  системы. 

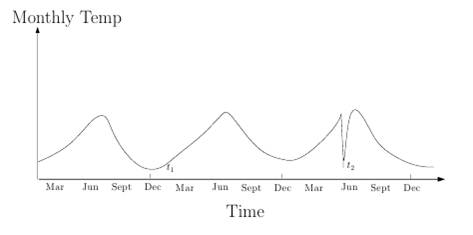
Рисунок  1.  Временной  ряд  температурной  динамики  с  наличием  аномального  участка

В  труде  [5,  с.  6]  выделяют  следующие  задачи  поиска  аномалий  на  дискретном  числовом  ВР:

1.  Задача  распознавания  аномалий,  вытекающих  из  контекста  наблюдаемого  процесса.

2.  Задача  выделения  аномальных  участков  и  дифференциация  аномалий  от  шумов.

3.  Задача  распознавания  аномалий  путем  сравнения  идеальных  и  реальных  процессов.

Каждой  представленной  выше  задаче  соответствует  ряд  проблем,  которые  могут  быть  в  той  или  иной  степени  решены  на  основе  математического  моделирования.

Так,  из  п.1  вытекает  проблема  масштабируемости  аномалий  (аномальным  может  являться  единичное  наблюдение;  аномальной  может  быть  локальная  или  основная  тенденция  ВР;  аномальным  может  быть  ВР  по  отношению  к  некоторому  множеству  нормальных  (без  аномалий)  ВР  описывающих  один  и  тот  же  процесс).  Из  п.  2  вытекает  проблема  невозможности  установления  абсолютно  точных  границ  аномальной  подпоследовательности  во  ВР,  а  также  задача  дифференциации  аномалий  от  шумов,  требующей  больших  вычислительных  затрат  прямо  пропорционально  длине  ВР.  Проблема  идентификации  причин  различий  идеальной  и  реальной  модели  ВР  вытекает  из  п.  3.

Общей  проблемой  поиска  аномалий  является  определение  наилучшей  меры  расстояния  (подобия)  для  разных  типов  ВР,  т.  к.  элементарную  меру  —  Евклидово  расстояние  не  всегда  удобно  использовать  в  условиях  ВР  разной  длины  и  больших  перепадов  значений  числовых  характеристик  (например,  макропоказателей  в  эконометрике)  [2,  с.  50].  Для  ВР  описывающих  сложные  процессы  с  большим  временем  протекания  возрастает  вычислительная  сложность  алгоритмов  обнаружения  аномалий. 

Для  поиска  аномалий  на  ВР  применимы  далеко  не  все  известные  методы  и  модели,  которые  справедливы  для  произвольных  числовых  совокупностей.  Выделим  следующие  основные  методы  обнаружения  аномалий  ВР  и  проблемы,  которые  они  решают  (табл.  1):  метод  скользящего  окна,  кластеризация,  статистические,  нечеткие.

Метод  скользящего  окна.  В  данном  методе  поиска  аномалий  ВР  разбивается  на  некоторое  число  подпоследовательностей  (окон).  Наиболее  эффективно  данная  методика  работает,  если  выбирается  окно  фиксированной  длины,  меньше  чем  длина  самого  ВР.  Поиск  аномальной  подпоследовательности  осуществляется  при  помощи  скольжения  окна  по  всему  ВР  с  шагом  меньшим  длины  окна  [5,  с.  19].  Однако  метод  имеет  ряд  недостатков.  Во-первых,  размер  окна  должен  быть  тщательно  выбран,  чтобы  захватить  аномалию  в  процессе  скольжения.  Во-вторых,  увеличение  во  ВР  количества  окон  при  разбиении  в  совокупности  с  длинной  ВР  значительно  повышают  вычислительную  сложность  алгоритма.  Однако  именно  этот  метод  является  самым  универсальным,  и  применим  для  любых  типов  ВР.

Кластеризация.  Кластеризация  являются  еще  одними  из  одних  универсальных  методов  поиска  аномалий.  Ограничением  методов  кластеризации  является  то,  что  они  способны  охарактеризовать  аномальный  ВР  целиком  и  не  дают  представления  о  точности  границ  аномальных  подпоследовательностей  (если  они  и  есть).  Также  эти  методы  практически  игнорируют  незначительные  аномалии  [5,  c.  23]

Статистические  методы.  В  статистических  методах  широко  используются  критерии  для  проверки  гипотез  о  сходстве  или  различии  двух  выборок.  Корреляционный  анализ  ориентирован  на  оценивание  статистической  связи,  и  факт,  что  эта  связь  между  идеальным  и  реальным  ВР  изменяется  может  служить  для  анализа  аномальности.  Данные  методы  хорошо  зарекомендовали  себя  в  решении  задач  поиска  аномалий  в  физических  процессах,  где  имеется  история  наблюдений. 

Таблица  1.

Задачи  и  методы  обнаружения  аномалий

Скрытые  модели  Маркова  (СММ).  Данная  модель  является  конечным  автоматом,  характеризующим  систему  по  его  наблюдаемым  параметрам.  В  основе  данного  метода  обнаружения  лежит  предположение  о  том,  существует  скрытый  Марковский  процесс,  который  генерирует  нормальный  ВР.  В  отсутствии  такого  процесса,  методика  не  будет  в  состоянии  отследить  аномалии.  Однако  если  построить  ВР  в  соответствии  с  Марковским  процессом,  то  можно  будет  отслеживать  аномалии  любого  масштаба  (единичные,  подпоследовательности,  всего  ВР).

Нечеткие  методы.  Класс  математических  моделей  основанных  на  нечетких  временных  рядах  (НВР)  описывает  динамику  процессов,  протекающих  в  условиях  неопределенности  при  помощи  специальных  нечетких  меток  [1,  c.  25].  Применение  нечетких  методов  обнаружения  аномалий  в  НВР  связано  с  задачей,  решаемой  в  ходе  экспертной  деятельности  —  диагностикой  процессов,  которые  описываются  этими  НВР.  Аномальными  могут  являться  следующие  типы  значений  нечеткого  временного  ряда:  уровни  исходного  ВР;  уровни  нечеткого  ВР;  нечеткие  элементарные  тенденции  (атомарные  нечеткие  термы);  нечеткие  локальные  тенденции;  синтаксические  правила;  НВР  в  целом.  Поиск  нетипичных  показателей  в  НВР  может  осуществляться  при  помощи  методов  частотного  или  синтаксического  анализа.  Последний  предусматривает  введение  нечеткого  языка  (нечеткой  грамматики)  и  распознавания  его  при  помощи  нечетких  конечных  автоматов.  Кроме  того,  отслеживание  аномалий  в  НВР  можно  свести  к  задачам,  решаемым  в  базисе  нечетких  тенденций  ранее  упомянутыми  методами  (скользящего  окна,  кластеризации  и  т.  д.)  с  осуществление  последующего  частотного  анализа  результатов  [1,  c.  258].

В  данной  работе  были  проклассифицированы  и  охарактеризованы  проблемы  и  основные  математические  методы  обнаружения  аномалий  в  одномерных  числовых  и  нечетких  ВР.  В  дополнение  к  вышесказанному  стоит  отметить,  что  в  настоящее  время  все  более  широкое  распространение  получают  именно  НВР,  а  также  многомерные  временные  ряды  (МВР),  где  проблемы  обнаружения  аномалий  в  достаточной  степени  еще  не  изучены.

Список  литературы:

1.Афанасьева  Т.В.,  Ярушкина  Н.Г.  Нечеткое  моделирование  временных  рядов  и  анализ  нечетких  тенденций.  Ульяновск:  УлГТУ,  2009.  —  299  с.

2.Шустенкова  Е.В.  Множественный  вейвлет-анализ  в  социологии.  Вестник  общественного  мнения.  —  №  2(94).  —  2008.  —  с.  49—59.  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ecsocman.hse.ru/data/2010/12/13/1214862070/7.pdf  (дата  обращения:  24.01.2014).

3.Ярушкина  Н.Г.,  Афанасьева  Т.В.  Нечеткие  временные  ряды  как  инструмент  для  оценки  и  измерения  динамики  процессов  /  Н.Г.  Ярушкина,  Т.В.  Афанасьева  //  Датчики  и  системы.  —  2007.  —  №  12.  —  С.  46—50.

4.Arindam  Banerjee,  Varun  Chandola,  Vipin  Kumar.  Anomaly  detection:  A  Survey.  Department  of  Computer  Science  and  Engineering  University  of  Minnesota.  —  2009.  —  73  с.  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.dtc.umn.edu/publications  /reports/2008_16.pdf  (дата  обращения:  24.01.2014).

5.Deepthi  Cheboli.  Anomaly  Detection  of  Time  Series.  Facility  Of  The  Graduate  School  Of  The  University  Of  Minnesota.  —  2010.  —  75  c.  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://conservancy.umn.edu/bitstream/11299/92985/1/Cheboli_Deepthi_May2010.pdf  (дата  обращения:  24.01.2014).