Статья опубликована в рамках: XXIX Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 29 января 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ СЕЗОННЫХ МЕТОДОВ АНАЛИЗА ВРЕМЕННЫХ РЯДОВ ДЛЯ ПРОГНОЗИРОВАНИЯ ОБЪЕМОВ ЭЛЕКТРОПОТРЕБЛЕНИЯ
Тонерян Мкртыч Саркисович
аспирант Ульяновского государственного технического университета, РФ, г. Ульяновск
EFFICIENCY RESEARCH OF SEASONAL METHODS OF TIME SERIES ANALYSIS FOR PREDICTING THE VOLUME OF POWER CONSUMPTION
Mkrtych Toneryan
postgraduate student of Ulyanovsk State Technical University, Russia Ulyanovsk
АННОТАЦИЯ
В настоящей работе описаны методы анализа сезонности временных рядов для прогнозирования объемов электропотребления. Проблема является актуальной, так как от затрат на электропотребление зависит бюджет предприятия, округа, региона в целом. Классические и современные подходы прогнозирования, в полной мере не могут отразить будущей картины факторов влияющих на данный процесс. Также, традиционные модели не предоставляют возможность в лингвистической форме получать и обрабатывать исторические данные.
ABSTRACT
This paper is devoted to methods of analysis for seasonal time series forecasting volumes of electricity. The problem is actual because of the cost of power consumption depends on the enterprise budget, county, region as a whole. Classical and modern approaches prediction fully may not reflect the future picture of factors affecting this process. Also, the traditional model does not provide the ability to linguistic form to receive and process history data.
Ключевые слова: временной ряд; сезонность; модели; нечеткие временные ряды.
Keywords: time series, seasonality; model; fuzzy time series.
В современном мире мы можем наблюдать за повторяющимися процессами через некоторые промежутки времени. Данный процесс выявляется в различных областях науки, однако, их исследование требует построения математических моделей временных рядов. На основе исторических данных этот процесс можно описать, тем самым выявить так называемую сезонность.
Современные методики анализа моделей с сезонной компонентой базируются на статистическом, нейросетевом и нечетком подходах.
Сезонные колебания исследованы в методиках статистического моделирования временных рядов. К наиболее простым моделям относятся моделирование на основе аддитивной (или мультипликативной) модели, содержащей трендовую и сезонную компоненты. Данные методы используют скользящие средние или методы оценивания регрессий для идентификации трендовой компоненты. Для учета влияния сезонности предварительно вычисляют индексы сезонности, которые затем используются для корректировки прогноза трендовой компоненты. Наиболее известные методы адаптивного прогнозирования временных рядов, к которым относятся модели Брауна (1959) [4], Хольта-Уинтерса (1960) и Тэйла-Вейджа (1964) (1). Имеется существенный недостаток данного подхода: результаты прогноза сильно зависят от параметра сглаживания или от вида уравнения регрессии.
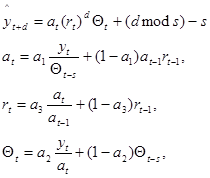 (1)
(1)
где: ![]() — текущая период сезонности
— текущая период сезонности ![]()
![]() — сезонный профиль ;
— сезонный профиль ;
![]() — параметр тренда;
— параметр тренда;
![]() —параметр прогноза очищенный от тренда и сезонности.
—параметр прогноза очищенный от тренда и сезонности.
К другим моделям анализа сезонных колебаний относится - спектральный анализ. Цель спектрального анализа — разложить ряд на функции синусов и косинусов различных частот, для определения тех, появление которых особенно существенно и значим. Однако этот подход имеет ограничения для анализа временных рядов в условиях небольшой длины, т. к. эмпирический анализ спектральной плотности требует в качестве своей информационной базы достаточно длинных стационарных временных рядов.
![]() (2)
(2)
где: ![]() — круговая частота;
— круговая частота;
Мультипликативная сезонная модель АРПСС(p,d,q)(ps,ds,qs) представляет естественное развитие и обобщение обычной модели АРПСС(p,d,q) [3] на ряды, в которых имеется сезонная компонента. В дополнении к несезонным параметрам, в модель вводятся сезонные параметры для определенного лага (устанавливаемого на этапе идентификации порядка модели). Однако из-за мощности и гибкости для построения подходящей модели АРПСС (3) требуется большая практика, результаты моделирования зависят от квалификации, которая определяет адекватную интерпретацию прогноза.
![]() (3)
(3)
где: ![]()
![]()
Наиболее распространенные модели анализа на основе искусственных нейронных сетей (Розенблатт, 1957) ориентированы на распознавание образов и требуют формирования обучающей выборки, которую сложно получить для временных рядов, обладающих высокой степенью неопределенности. Также модели временных рядов на основе искусственных нейронных сетей невозможно интерпретировать в терминах предметной области.
Модели и методы нечеткого подхода показали свою результативность и высокую интерпретируемость при анализе временных рядов небольшой длины в образовании и экономике. Теоретические основы нечеткого подхода заложил Л. Заде (1965), которые привели с созданию в дальнейшем модели нечеткого временного ряда [6] и модели нечеткой тенденции [1]. Однако научные основы нечеткого подхода не учитывают возможность идентификации сезонных изменений, наблюдаемых в социальных и экономических процессах.
![]() (4)
(4)
где: d — фиксированное число, параметр модели;
![]() — последовательность нечетких тенденций;
— последовательность нечетких тенденций;
![]() — некоторая нечеткая зависимость.
— некоторая нечеткая зависимость.
С помощью программного продукта BESTS [2] был произведен ряд экспериментов в области электропотребления с реальными числовыми данными действующего предприятия Ульяновской области. При построении исходного ряда, которого можно наблюдать сезонность. Исторические данные предприятия за 40 месяцев, поэтому можно строго определить их как данные с высокой степенью неопределенности.
Таблица 1.
Таблица внутренних и внешних критериев оценки модели
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Несмотря на обилие моделей различных подходов как описывалось выше, мы видим, что они не лишены недостатков, самым главным из которых является ограничение при анализе временных рядов обладающих высокой степенью неопределенности. Тот факт, что нечеткий подход хорошо зарекомендовал себя, в данной области решения говорит о полезности выявления одной из проблем нечетких моделей, а именно — сезонность.
Судя по таблице, лучшая модель для оценки точности является — модель нечетких тенденций. Ранее в работах Ярушкиной Н.Г. и Афанасьевой Т.В. [5] отмечалось, что модель, основанная на нечетких правилах следования нечетких тенденций, не генерирует правила для сезонных компонент ВР, поэтому получаемые результаты не достаточно точны, но, тем не менее, демонстрируют лучший результат для прогнозирования объема электропотребления предприятия.
Список литературы:
1.Афанасьева Т.В. Нечеткое моделирование временных рядов и анализ нечетких тенденций / Т.В. Афанасьева, Н.Г. Ярушкина. Ульяновск: УлГТУ, 2009. — 299 с.
2.Афанасьева Т.В., Тонерян М.С. Комплекс программ анализа временных рядов BESTS / VII Всероссийская научная конференция «Математическое моделирование развивающейся экономики, экологии и биотехнологий», ЭКОМОД 2012, г. Киров, 2—8 июля 2012 / Сборник тезисов. Киров, изд-во ВятГУ, 2012. — С. 14.
3.Бокс Дж., Дженкинс Г. Анализ временных рядов, прогноз и управление /Дж. Бокс, Г. Дженкинс/ М.: Мир, 1974. — 197 с.
4.Лукашин Ю.П., Адаптивные методы краткосрочного прогнозирования временных рядов. М.: Финансы и статистика, 2003. — 416 с
5.Ярушкина Н.Г., Афанасьева Т.В., Тонерян М.С. Применение нечетко-гранулярного моделирования числовых временных рядов / НАУЧНО-ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ. СЕРИЯ 2: ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ И СИСТЕМЫ: Всероссийский институт научной и технической информации РАН (Москва), 2013 — С. 35—41.
6.Song Q., Chissom B. Fuzzy time series and its models // Fuzzy Sets and Systems. — 1993. — № 54. — Р. 269—277.
дипломов


Оставить комментарий