ПРОГНОЗИРОВАНИЕ  МЕХАНИЧЕСКИХ  СВОЙСТВ  СИНТЕТИЧЕСКИХ  ПОЛИМЕРНЫХ  ПЛЕНОК  И  НИТЕЙ  В  РЕЖИМЕ  РЕЛАКСАЦИИ  НАПРЯЖЕНИЯ

Рымкевич  Павел  Павлович

канд.  физ.-мат.  наук,  проф.  Военно-Космической  Академии  им.  А.Ф.  Можайского,  РФ,  г.  Санкт-Петербург

E-mail:  pprymkevich@gmail.com

Романова  Алла  Александровна

канд.  тех.  наук,  доц.  СПб  Государственного  университета  сервиса  и  экономики,  РФ,  г.  Санкт-Петербург

E-mail:  romallaa@yandex.ru

Головина  Виктория  Владимировна

преподаватель  Военно-Космической  Академии  им.  А.Ф.  Можайского,  РФ,  г.  Санкт-Петербург

Коцкович  Владимир  Богданович

канд.  тех.  наук,  доц.  СПб  Государственного  университета  сервиса  и  экономики,  РФ,  г.  Санкт-Петербург

Кикец  Евгений  Викторович

канд.  тех.  наук,  доц.  СПбГ  государственного  университета  технологии  и  дизайна,  РФ,  г.  Санкт-Петербург

FORECASTING  OF  MECHANICAL  PROPERTIES  OF  SYNTHETIC  POLYMERIC  FILMS  AND  YARNS  DURING  STRESS  RELAXATION

Pavel  Rymkevich

candidate  of  Physical  and  Mathematical  Sciences,  professor  of  Mozhaisky  Military  Space  Academy,  Russia  Saint  Petersburg

Alla  Romanova

candidate  of  Science,  associate  professor  of  Saint  Petersburg  State  University  of  Service  and  Economics,  Russia  Saint  Petersburg

Viktoria  Golovina

teacher  of  Mozhaisky  Military  Space  Academy,  Russia  Saint  Petersburg

Vladimir  Kotskovich

candidate  of  Science,  associate  professor  of  Saint  Petersburg  State  University  of  Service  and  Economics,  Russia  Saint  Petersburg

Evgeny  Kikets

candidate  of  Science,  associate  professor  of  Saint-Petersburg  State  University  of  Technology  and  Design,  Russia  St.  Petersburg

АННОТАЦИЯ

На  основании  физической  теории  строения  одноосноориентированных  полимерных  материалов  предложена  новая  механическая  модель,  позволяющая  прогнозировать  релаксационные  процессы  в  полимерах.  Выводы,  вытекающие  из  разработанной  математической  модели,  подтверждены  на  примере  поликапроамидных  пленочных  нитей  разной  степени  вытяжки,  а  также  на  примере  нитрона  и  полиэтилентерефталата  при  разных  значениях  температуры.

ABSTRACT

Based  on  the  physical  theory  of  structure  of  uniaxially  oriented  polymeric  materials  there  has  been  presented  a  new  mechanical  analogue  enabling  to  forecast  relaxation  processes  in  polymers.  Conclusions  of  the  worked  out  mathematical  model  have  been  proved  by  the  example  of  polycaproamide  tape  yarns  of  various  drawing  ratio  and  also  by  the  example  of  nitrone  and  polyethylene  terephthalate  at  different  temperatures. 

Ключевые  слова:  потенциальный  барьер;  ориентированные  полимеры;  нелинейная  вязкоупругость;  поликапроамид;  релаксация  напряжения

Keywords:  potential  barrier;  oriented  polymers;  nonlinear  viscoelasticity;  polycaproamide;  stress  relaxation. 

В  настоящее  время  трудно  найти  отрасль  промышленности,  которая  не  использовала  бы  синтетические  полимерные  материалы  и  изделия  на  их  основе.  При  этом  технический  прогресс  ставит  задачи  как  получения  новых  материалов,  так  и  повышения  ресурсов  работы  традиционных  материалов,  разработки  оптимальных  режимов  эксплуатации  и  разработки  методов  прогнозирования  работоспособности.

Расширение  областей  применения  и  условий  эксплуатации  полимерных  материалов,  а  также  их  незаменимость  в  большинстве  изделий  бытового  и  технического  назначения  требует  качественного  исследования  их  вязкоупругих  свойств.  И  прежде  всего,  это  достаточно  глубокое  количественное  описание  деформационных  свойств  в  зоне  действия  неразрушающих  механических  нагрузок.  Такие  исследования  возможны  на  основе  математического  моделирования  процессов  деформирования. 

Анализ  существующих  методов  математического  моделирования  показывает,  что  сегодня  на  практике  для  количественного  прогнозирования  поведения  полимерных  материалов  применяются  методы,  в  основе  которых  лежат  уравнения,  полученные  при  использовании  классических  линейных  механических  моделей  в  виде  гуковских  пружин,  демпферов  и  их  комбинаций,  то  есть  классических  линейных  элементов  Максвелла,  Кельвина-Фойгта  и  др.  При  этом  большинство  полимерных  материалов  (например,  синтетические  волокна,  нити  и  пленки)  уже  на  начальном  этапе  механических  воздействий  проявляют  нелинейные  реологические  свойства.  Для  полимерных  материалов  с  таким  поведением  разработан  ряд  теорий  нелинейной  вязкоупругости  [2,  4,  5,  7,  8,  10,  13].  Подобные  теории  нелинейной  вязкоупругости  строятся  посредством  обобщения  уравнений  линейной  вязкоупругости  с  помощью  известных  представлений  о  температурно-сило-деформационно-временных  аналогиях,  однако,  применимы  в  достаточно  узком  диапазоне  механических  нагрузок,  деформаций  и  температур,  и  не  позволяют  предсказать  некоторые  особенности  поведения  полимерных  материалов.  Кроме  того,  в  интегральных  уравнениях  вязкоупругости  [1,  2,  4—9,  12,  13]  не  учитываются  физические  особенности  полимеров.

Анализ  экспериментальных  данных  по  исследованию  процессов  ползучести  и  релаксации  механического  напряжения  позволяет  сделать  вывод  о  справедливости  температурно-сило-временной  аналогии  при  описании  процесса  ползучести  и  температурно-деформационно-временной  аналогии  при  описании  процесса  релаксации  механического  напряжения  применительно  к  большинству  полимерных  объектов.  Однако  само  существование  этих  аналогий  требует  построения  физической  теории,  позволяющей  не  только  описать  деформационные  процессы  с  позиции  современных  представлений  о  кинетической  природе  микромеханизмов  деформирования,  но  и  указать  пределы  применимости  методов,  построенных  на  тех  или  иных  аналогиях.

Поэтому  в  работе  при  моделировании  деформационных  и  релаксационных  процессов  используется  нелинейная  механическая  модель,  учитывающая  физические  особенности  полимерных  материалов.

Известно,  что  полную  деформацию  ε  можно  представить  в  виде  суммы  упругой  (ε_упр),  вязкоупругой  или  конформационной  (ε_конф)  и  необратимой  (ε_необр)  частей  деформации,  а  именно:

.                      (1)

При  деформировании  полимеров  особого  внимания  заслуживает  обратимая  вязкоупругая  составляющая  деформации.

В  нагруженном  состоянии  полимеры  могут  находиться  в  различных  квазиравновесных  состояниях.  Согласно  современной  физической  картине  вязкоупругая  составляющая  деформации  может  появиться  вследствие  перестроек  различных  устойчивых  структур  (кластеров),  находящихся  в  состояниях,  которые  разделены  энергетическими  барьерами  [3,  10,  11,  14].  Эти  кластеры  или  активные  конформационные  элементы  (АКЭ)  [10],  природа  которых  для  механического  описания  не  имеет  существенного  значения,  могут  находиться  в  двух  устойчивых  состояниях,  разделенных  энергетическим  барьером  высотой    и  шириной  .  То  есть  механическая  модель  представляет  собой  упругую  пружинку,  которая  может  находиться  либо  в  свернутом,  либо  в  развернутом  состоянии.  Таким  образом,  вместо  классических  механических  моделей,  состоящих  из  гуковских  пружин,  демпферов  и  их  комбинаций,  используется  нелинейная  модель  в  виде  упругой  пружинки,  основанная  на  энергетических  барьерах.

Необратимую  часть  деформации  будем  рассматривать  как  принципиально  обратимую,  но  при  высоких  температурах.  В  данной  работе  будет  рассмотрена  только  обратимая  часть  деформации,  т.  е.  в  соотношении  (1)  принимается  .

Переход  из  одного  устойчивого  состояния  в  другое  сопровождается  квантом  деформации  .  При  таком  подходе  вязкоупругая  часть  деформации  ε_конф  лимитируется  обратимыми  переходами  АКЭ  из  одного  состояния  в  другое.

Таким  образом,  используется  модель  в  виде  упругой  нелинейной  пружины  с  двумя  устойчивыми  состояниями,  разделенными  энергетическим  барьером,  и  подчиняющимися  законам  статистической  механики.

Наличие  такой  пружинки  дает  возможность  описать  всю  совокупность  свойств  полимерных  материалов.  И  в  результате  анализа  всей  системы,  с  учетом  больцмановского  заполнения  уровней,  подсчета  числа  переходов,  учета  неравномерности  распределения  нагрузки  по  образцу  вместо  интегральных  уравнений  [4—7,  12]  описание  реологического  поведения  одноосноориентированного  полимерного  материала  сводится  к  решению  системы  двух  обыкновенных  дифференциальных  уравнений.  Эти  уравнения  связывают  между  собой  деформацию    (режим  деформирования),    —  усредненное  механическое  напряжение  внутри  образца  и  усредненную  поправку  к  механическому  напряжению  .  Окончательно,  данную  систему  уравнений  можно  представить  в  виде  [3,  14]:

,                                         (2)

где 

.

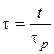  —  безразмерное  время; 

  —  внутреннее  время  релаксации,  определяемое  высотой  барьера;

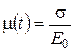  —  механическое  напряжение,  приложенное  ко  всему  образцу,  то  есть  величина,  непосредственно  определяемая  из  эксперимента;

  —  структурно-чувствительный  коэффициент,  который  определяется  упругой  энергией  АКЭ,    —  приведенный  структурно-чувствительный  коэффициент;

;

  и    —  соответственно  среднее  значение  и  дисперсия  случайной  величины  ;

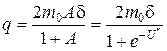  —  константа  материала,  слабо  зависящая  от  температуры;

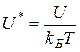и    —  приведенная  высота  энергетического  барьера  и  приведенная  ширина  энергетического  зазора,  соответственно.

Однако  для  исследуемых  процессов  деформирования  можно  пренебречь  малой  поправкой  пропорциональности  .  Тогда  система  уравнений  (2)  сведется  к  одному  обыкновенному  дифференциальному  уравнению  вида:

.          (3)

В  рамках  данной  работы  рассмотрим  режим  релаксации  напряжения.

Применим  определяющее  уравнение  в  форме  (2)  для  режима  релаксации  напряжения  при  условии  .  Начальное  условие    ()  зависит  от  начальной  скорости  деформирования.  Уравнение  (3)  при  этих  условиях  примет  вид:

.                           (4)

Общий  интеграл  этого  уравнения  имеет  следующий  вид:

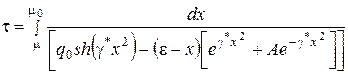.                         (5)

Непосредственное  исследование  интеграла  (5)  затруднительно,  так  как  он  не  выражается  через  элементарные  функции.  Поэтому  исследуем  отдельные  предельные  случаи.  Для  малых  времен,  соизмеримых  со  временем  релаксации,  (ε-μ)  мало  и  интеграл    полностью  определяется  правой  частью  уравнения  (4),  то  есть:

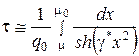.                                       (6)

И  в  случае  не  очень  высоких  напряжений  .  Тогда 

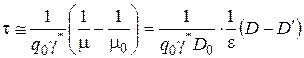.                         (7)

Здесь    —  податливость    в  момент  времени    и    —  податливость  в  начальный  момент  времени.  Отсюда  вытекает  следующая  зависимость  изменения  податливости  от  деформации  за  фиксированный  одинаковый  промежуток  времени:

,  (8)

где  .

Этот  теоретический  результат  подтвержден  экспериментальными  данными,  полученными  в  результате  исследования  поликапроамидных  (ПКА)  пленочных  нитей  в  режиме  релаксации  напряжения.  С  этой  целью  были  взяты  значения  релаксирующего  модуля  для  моментов  времени  6  и  15  секунд  на  разных  уровнях  деформирования.  Тогда  в  результате  вычислений  по  формуле  (8)  с  учетом  того,  что  ,  получены  зависимости  изменения  податливости  от  деформации  за  промежуток  времени  9  секунд  для  ПКА  пленочных  нитей  разной  степени  вытяжки,  приведенные  на  рис.  1. 

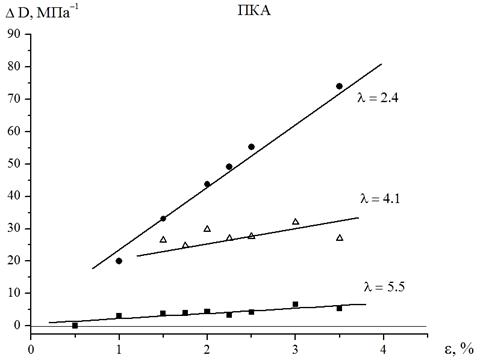
Рисунок  1.  Зависимость  изменения  податливости  от  деформации  за  промежуток  времени  Dt  =  9''  для  ПКА  пленочных  нитей  разной  степени  вытяжки

Согласно  рис.  1  видно,  что  линейная  зависимость  выполняется.  К  тому  же  с  помощью  полученной  зависимости  можно  прогнозировать  процесс  деформирования  при  достаточно  малых  временах,  то  есть  в  моменты  времени,  когда  процесс  идет  интенсивно,  и  «вырабатывается»  порядка  95  %  всей  ползучести. 

Аналогичные  вычисления  были  проведены  на  других  полимерных  материалах.  На  рис.  2  приведены  зависимости  изменения  податливости    за  одинаковые  промежутки  времени  для  синтетической  нити  нитрон  при  значениях  температуры  окружающей  среды  Т  =  20  °С;  40  °С;  60  °С.  А  на  рис.  3  приведены  зависимости  изменения  податливости    за  одинаковые  промежутки  времени  для  синтетической  нити  из  полиэтилентерефталата  при  значениях  температуры  окружающей  среды  Т  =  20  °С;  40  °С;  60  °С  и  80  °С.  Согласно  полученным  зависимостям  видно,  что  линейная  зависимость  между  рассматриваемыми  величинами  также  выполняется  и  дает  возможность  прогнозировать  процесс  деформирования  при  малых  временах  нагружения.

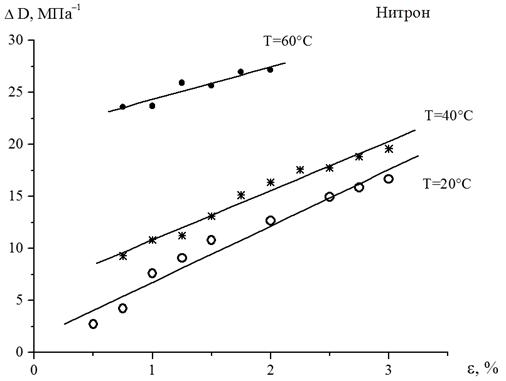
Рисунок  2.  Зависимость  изменения  податливости  от  деформации  за  промежуток  времени  Dt  =  9''  синтетической  нити  нитрон  при  разных  значениях  температуры

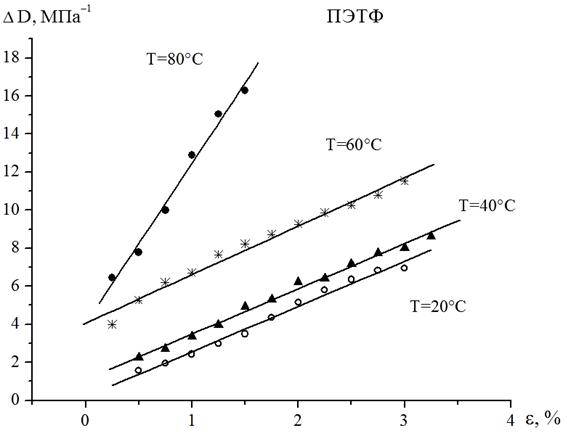
Рисунок  3.  Зависимость  изменения  податливости  от  деформации  за  промежуток  времени  Dt  =  9''  полиэтилентерефталата  в  виде  синтетической  нити  при  разных  значениях  температуры

Таким  образом,  на  основании  полученных  зависимостей  можно  прогнозировать  деформационное  поведение  одноосноориентированных  синтетических  полимерных  материалов  в  режиме  релаксации  при  коротких  временах  воздействия. 

Список  литературы:

1.Бугаков  И.И.  Исследование  взаимодействия  между  нелинейными  уравнениями  вязкоупругости,  основанными  на  принципе  сложения  //  Вестник  ЛГУ.  Матем.,  Механ.  —  1987.  —  №  8.  —  Вып.  2.  —  С.  47—51.

2.Вязкоупругие  свойства  полимеров  /  Дж.  Ферри.  М.:  Наука,  1970.  —  535  с.

3.Головина  В.В.  Физико-механическая  модель  одноосноориентированного  полимерного  материала  /  В.В.  Головина,  П.П.  Рымкевич,  А.А.  Романова,  В.Б.  Коцкович  //  Естеств.  и  матем.  науки:  Акт.  вопросы  и  тенденции  развития:  Мат-лы  междунар.  научно-практич.  конф.  4—9.02.2013.  Новосибирск:  Изд-во  «СибАК»,  2013.  —  С.  25-38.

4.Демидов  А.В.  Вариант  моделирования  нелинейно-наследственной  вязкоупругости  полимерных  материалов  /  А.В.  Демидов,  А.Г.  Макаров,  А.М.  Сталевич  //  Известия  РАН.  Механика  твердого  тела.  —  2009.  —  №  1.  —  С.  155—165.

5.Деформирование  ориентированных  полимеров  /  А.М.  Сталевич.  СПб.:  Изд-во  СПГУТД,  2002.  —  250  с.

6.Методы  математического  моделирования  механических  свойств  полимеров  /  А.Г.  Макаров,  А.В.  Демидов.  СПб.:  Изд-во  СПб  гос.ун-та  технологии  и  дизайна,  2009.  —  392  с.

7.Методы  прикладной  вязкоупругости  /  А.А.  Адамов,  В.П.  Матвеенко,  Н.А.  Труфанов,  И.Н.  Шардаков.  Екатеринбург:  УрО  РАН,  2003.  —  411  с.

8.Механические  свойства  высокополимеров  /  Т.  Алфрей.  М.:  ИЛ  1952.  —  720  с.

9.Ползучесть  полимерных  материалов  /  И.И.  Бугаков.  М.:  Наука,  1973.  —  288  с.

10.Рымкевич  П.П.  Кинетическая  теория  конформационных  переходов  в  полимерах  /  П.П.  Рымкевич,  А.М.  Сталевич  //  Физико-химия  полимеров  /  Сб.научн.тр.Тверской  гос.ун-т.  Вып.  5.  Тверь,  1999.  —  С.  52—58.

11.Рымкевич  П.П.  Физические  основы  вязкоупругого  поведения  ориентированных  аморфно-кристаллических  полимеров  /  П.П.  Рымкевич,  А.А.  Романова,  А.С.  Горшков,  А.Г.  Макаров  //  Известия  вузов.  Технология  легкой  промышленности.  —  2012.  —  №  2.  —  С.  70—73.

12.Сталевич  А.М.  Простейший  вариант  наследственного  ядра  релаксации  ориентированного  аморфно-кристаллического  полимера  /  А.М.  Сталевич,  А.Г.  Макаров  //  Физико-химия  полимеров  /  Сб.  научн.  тр.  Тверской  гос.ун-т.  Вып.  5.  Тверь,  1999.  —  С.  58—64.

13.Элементы  наследственной  механики  твердых  тел  /  Ю.Н.  Работнов.  М.:  Наука,  1977.  —  384  с.

14.Rymkevich  P.P.  The  energy  barriers  model  for  physical  description  of  viscoelasticity  of  synthetic  polymers:  application  to  the  uniaxial  orientational  drawing  of  polyamide  films  /  P.P.  Rymkevich,  A.A.  Romanova,  V.V.  Golovina,  and  A.G.  Makarov  //  J.  of  Macromolecular  Science,  Part  B:  Physics,  2013,  52,  —  С.  1—19.