ПРЕДСТАВЛЕНИЕ  И  ОБРАБОТКА  ЗНАНИЙ  В  ГИБРИДНЫХ  ИНФОРМАЦИОННЫХ  АВТОМАТИЗИРОВАННЫХ  СИСТЕМАХ

Мазаков  Евгений  Борисович

канд.  техн.  наук,  зав.  кафедрой  информационных  систем  и  вычислительной  техники,  доцент  Национального  минерально-сырьевого  университета  «Горный»,  г.  Санкт-Петербург

E-mail: 

REPRESENTATION  AND  PROCESSINGKNOWLEDGE  IN  HYBRIDAUTOMATEDINFORMATIONSYSTEMS

Evgeny  Mazakov

Candidate  of  Science,  Head  of  Information  Systemsand  Computer  Engineering,  associate  professor  of  nationalresources  Mineral  University,  Sankt-Peterburg

АННОТАЦИЯ

Рассматривается  подход  к  построению  базы  знаний  с  использованием  теории  категорий,  аксиоматических  формальных  теорий  и  аппарата  топологической  булевой  алгебры.  Показана  возможность  обрабатывать  нечеткую  информацию  и  осуществлять  логический  вывод  в  рамках  дедуктивных  формальных  систем. 

ABSTRACT

The  approach  to  construction  of  the  knowledge  base  with  use  of  the  theory  of  categories,  axiomatic  formal  theories  and  the  device  topological  Boolean  algebra  is  considered.  The  possibility  to  process  fuzzy  information  and  carry  out  the  logical  conclusion  in  the  formal  deductive  systems.

Ключевые  слова:  нефтегазовая  отрасль,  интеллектуальное  месторождение,  база  знаний,  формальная  система,  топологическая  булева  алгебра.

Keywords:  oil  and  gas  industry,  intellectual  field,  knowledge  base,  formal  system,  topological  boolean  algebra. 

Информационные  системы  и  технологии  служат  основой  развития  стратегически  важных  отраслей  минерально-сырьевого  комплекса  для  повышения  эффективности  за  счет  повышения  уровня  автоматизации  управления  разработкой,  оперативного  принятия  решений,  оценки  и  минимизации  рисков. 

В  настоящее  время  спрос  [3]  на  финансово-логистические  модули  ERP-систем,  наблюдавшийся  в  предыдущие  годы,  в  частности  в  нефтегазовом  секторе,  прошел.  Практически  на  всех  крупных  предприятиях  отрасли  уже  осуществляются  проекты  по  внедрению  ERP-решений,  и  сегодня  речь  идето  расширении  их  функциональных  возможностей,  разработке  новых  модулей,  связанных  с  управлением  человеческими  ресурсами,  активами,  сбытом  и  т.  д.  В  то  же  время,  все  большую  актуальность  приобретают  автоматизация  различных  технологических  процессов,  а  также  обеспечение  взаимодействия  между  управленческими  системами  верхнего  уровня  (класса  ERP)  и  системами  автоматизации  технологических  процессов  (АСУТП).  В  связи  с  чем  возник  активный  спрос  на  системы  промежуточного  уровня  (MES-системы),  обеспечивающие  эту  взаимосвязь,  интеграции  ключевых  ИТ-решений,  внедренных  на  различных  предприятиях. 

Кроме  того,  увеличивается  спрос  на  различные  аналитические  системы,  прежде  всего  решения  на  базе  OLAP-технологий  (интеллектуальный  анализ  данных),  позволяющих  обрабатывать  большие  объемы  данных  по  различным  срезам  на  уровне  централизованного  сбора  и  обработки  информации  в  рамках  всей  распределенной  структуры  управления.

Для  объединения  существующих  информационных  технологий  в  России  и  в  мире  (табл.  1)  начинают  внедрять  концепцию  (технологию)  «интеллектуальное  месторождение».  В  различных  источниках  наряду  с  термином  «интеллектуальное  месторождение»  используются  понятия  «умное  производство»,  «интеллектуальная  скважина»  и  др.

Таблица  1.

Объекты  интеллектуальных  месторождений

Под  интеллектуальным  нефтегазовым  месторождением  следует  понимать  [1]  систему  автоматического  (автоматизированного)  управления  операциями  по  добыче  нефти  и  газа,  предусматривающую  непрерывную  в  реальном  масштабе  времени  оптимизацию  интегральной  модели  месторождения  и  модели  управления  добычей,  гарантирующей  оптимальное  управление  на  всех  уровнях  при  контроле  целей  предприятия.

Необходимыми  условиями  существования  интеллектуального  месторождения  является:  формализованность  информационной  модели  месторождения,  наличие  аппарата  управления,  максимально  точные  интерфейсы  обратной  связи,  интерфейсы  для  оптимизации  процессов,  моделей  и  критериев.  В  структуре  интеллектуального  месторождения  можно  выделить  уровни  иерархии  (табл.  2)  и  их  взаимодействие  (рис.  1). 

Таблица  2.

Уровни  иерархии  интеллектуального  месторождения

Обработка  информации  и  управление  интеллектуальными  месторождениями  осуществляется  с  использованием  гибридных  автоматизированных  информационных  систем  (ГАИС),  которые  имеют  следующие  особенности:

решаются  различные  по  содержанию  и  применяемым  методам  задачи  —  информационно-поисковые,  расчетные,  аналитические,  логические  (интеллектуальные),  телекоммуникационные  и  др.;

значительный  объем  как  первичных  измерений,  так  и  результатов  моделирования  (может  составлять  десятки  теробайт);

большое  количество,  не  всегда  синхронизированных  между  собой,  моделей,  специального  математического  и  программного  обеспечения;

функционирование  происходит  в  условиях  неопределенности  и  неполноты  информации. 

Рисунок  1.Структура  и  взаимодействие  уровней  интеллектуального  месторождения

Как  показывает  анализ  [2,  с.  288],  традиционные  подходы  к  разработке  математического  и  программного  обеспечения  ГАИС  по  обработке  информации,  в  том  числе  и  технологии  «интеллектуальных  месторождений»,  не  дают  требуемых  результатов.

Ряд  последних  исследований  по  системам  обработки  информации  (данных,  знаний)  показывают,  что  существующие  методы  представления  и  обработки  знаний  основывались  на  теоретико-множественном  подходе,  который  ограничивает  возможности  по  манипулированию  знаниями.  Это  связано  со  следующими  причинами.

1.  Элементы  математических  множеств  не  оцениваются  по  присутствию.  В  реальности  присутствие  объектов  множеств  может  меняться  в  зависимости  от  состояния  предметной  области.

2.  Предметы,  как  элементы  множества,  и  сами  множества  являются  статичными  (не  меняющимися  с  течением  времени),  что  теряет  свое  значение  при  рассмотрении  реальных  физических  объектов.

Теория  категорий,  развивающаяся  в  последнее  время,  является  альтернативной  теории  множеств,  обладает  более  широкими  возможностями  по  описанию  реальных,  а  не  математических  объектов.  Среди  основных  преимуществ  теории  категорий  можно  выделить  следующие.

1.  Широкая  трактовка  категории  и  ее  объектов  как  свойств,  процессов,  состояний  и  явлений.  Объектами  категорий  могут  являться  не  только  множества,  но  и  другие  математические  абстракции  (универсальные  алгебры,  их  частные  примеры  и  др.).  Категория  представляет  универсальный  формализм,  позволяющий  с  единых  позиций  описывать  внешне  различные  объекты.

2.  Морфизмы  категорий  обозначают  морфизмы  вложения  (включения  в  класс),  функциональные  отображения  одних  объектов  в  (на)  другие,  а  это  позволяет  выразить  любые  связи  между  объектами.

Каждому  морфизму  категории  Kat  ставится  в  соответствие  синтаксическая  конструкция  вида

,

где:  —  имя  морфизма, 

Y  —  оригинал  Orig, 

Х  —  образ  Im.  Предполагается,  что  все  объекты  представляются  совокупностями  морфизмов.

Исходя  из  изложенного,  предлагается  категорная  модель  знаний  (КМ3).  Под  КМ3  понимается  совокупность  формализованных  описаний  объектов  и  закономерностей  проблемной  области,  а  также  эвристик,  воспроизводящих  целенаправленную  мыслительную  деятельность  эксперта  по  обработке  информации  и  принятия  решения. 

Вся  реальная  предметная  область  представляется  в  виде  объектов.  Объект  служит  для  моделирования  знаний  эксперта  об  отдельном  фрагменте  решаемой  задачи  в  виде  структур,  наиболее  полно  сохраняющих  семантику  ПО. 

Каждая  из  категорий  отражает  определенный  аспект  знаний  о  концептах  (интенсионал,  состояние,  пространство,  время  и  т.  п.).  Полное  описание  концепта  можно  представить  в  виде  произведения  категорий

.

Состав  категории  меняется  в  зависимости  от  рассматриваемого  «возможного  мира»  ω_i.  Множества  возможных  миров  связаны  между  собой  отношением  доступности  (R).  При  этом  пара  (ω,  К)  будет  представлять  метазнания  о  проблемной  области. 

Необходимо  заметить,  что  в  качестве  информации,  характеризующей  объект,  могут  выступать  признаки,  являющиеся  в  свою  очередь  концептами.  Объекты,  существенные  признаки  которых  являются  в  свою  очередь  концептами,  в  дальнейшем  будем  именовать  составными  объектами  (СО),  а  объекты,  описанные  только  через  индивидуальные  признаки  —  терминальными  объектами  (ТО).  Таким  образом,  СО  могут  состоять  из  признаков,  терминальных  объектов  и  других  составных  объектов.

Для  формализации  знаний  целесообразно  использовать  семиотический  подход.  При  этом  семиотическая  модель  ПО  строится  на  базе  формальной  системы  логического  типа  (логического  исчисления).  В  ряде  исследований  [4,  с.  112]  показано,  что  для  описания  объектов  реальности  наиболее  целесообразным  является  использование  исчисления,  построенного  на  базе  логики  присутствия  и  имеющее  следующие  особенности.

1.  В  данном  исчислении  понятие  свойства  принимается  в  качестве  первичного,  а  это  согласуется  с  теоретико-категорным  подходом  к  построению  КМЗ.

2.  Логические  операции  представлены  операциями  топологической  булевой  алгебры

,  (1)

где:    —  неисключающее  «ИЛИ»  по  присутствию, 

  —  соединение  по  при­сутствию, 

  —  релевантное  логическое  следование  по  присутствию, 

  —  дополнение  по  присутствию, 

I  и  С  —  взятие  внутренности  и  замыкания.

3.  Присутствие  объекта  определяется  с  использованием  констант  исчисления,  обозначающих  присутствие  Р_r,  отсутствие  А_b,  неопределенность  U_n,  противоречие  С_n.

В  соответствии  с  категорной  моделью  знаний  объекты  категорий  могут  быть  двух  типов  составные  и  терминальные.  В  зависимости  от  уровня  детализации  имеющихся  знаний  составной  объект  может  стать  терминальным,  а  терминальный  —  составным.  Это  зависит  от  того,  на  каком  уровне  получены  исходные  данные  от  датчиков  или  заданы  экспертом. 

В  исчислении  присутствия  любой  объект  описывается  через  некоторые  признаки  μ₁,  существенные  для  описания  объекта  в  мире  ω_i  согласно  теории  Т_k.  Основу  исчисления  составляет  понятие  присутствия  объекта  в  мире  ω,  принимающее  одно  из  двух  значений  присутствия  S(ω_i,T_k)и  N(ω_i,T_k).Первое  обозначает  присутствие  объекта  в  мире  ω_i  согласно  теории  Т_k,  второе  —  его  отсутствие. 

Так  как  объекты  имеют  материальную  основу  и  характеризуются  набором  признаков  (свойств),  то  формула  любого  произвольного  объекта  будет  представляться  через  признаки  на  языке  алгебры  (1)  в  виде

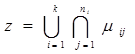  ,  (2)

где:  μ_ij  означает  некоторое  свойство  или  его  дополнение  по  присутствию; 

k,  n  —  соответственно,  количество  наборов  признаков  и  число  признаков  в  каждом  наборе.

Особенности  управления  в  сложных  организационно-технических  системах,  связанные,  прежде  всего,  с  неопределенностью  приводят  к  тому,  что  часть  признаков  могут  быть  недоступны  для  регистрации,  поэтому  их  можно  разделить  на  два  класса;  доступные  для  системы  π_ij  и  недоступные  —  ξ_ij.  Тогда  формула  терминального  объекта  примет  вид 

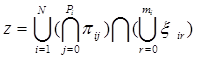  (3)

где:  P_i  +m_i  =  n_i,  .  При  этом  ξ_i0  и  π_i0  обозначают  S(ω,  T_i)  для  всех  .

Если  считать  значения  присутствия  признаков  ξ_ir  неизвестными,  то  придавая  каждому  из  них  значения  S(ω_{1  ,}T₁)и  N(ω_1,T₁)  во  всех  возможных  комбинациях  и  исключая  из  (3)  элементы,  для  которых  ,  получим  множество  формул  ψ_z,  каждая  из  которых  может  рассматриваться  как  окрестность  исходной  формулы.  На  множестве  ψ_z  можно  ввести  отношение  частич­ного  порядка  и  выделить  наибольшую  нижнюю  и  наименьшую  верхнюю  грани,  которые  принимаются,  соответственно,  в  качестве  внутренности  I_z  и  замыкания  C_z  формулы  .

Необходимо  заметить,  что  оценки  (val)  присутствия  объекта  z-  valz,  valz  для  произвольной  формулы  ϕ_z  выражаются  различными  формулами  —  Iz,  Сz,  Iz.,  Сz,  которые  могут  принимать  одно  из  значений:  S(ω_,  T₁)  или  N(ω_,  T₁)  и  являются  внутренними  константами  исчисления  присутствия.

В  соответствии  с  этим  объекту  z  ставится  в  соответствие  вектор  условий  присутствия  <Iz,  Сz,  Iz.,  Сz>,  оценки  которого  принимают  значения  из  следующей  совокупности

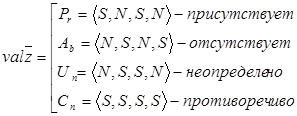
Если  I  интерпретировать  как  оператор  необходимости  L,  а  С-возможности  N,  то  исчисление  присутствия  может  быть  отнесено  к  модальной  логике  Льюиса.  Тогда,  например,  условие  «необходимо  z  и  возможно  z»  соответствует  достоверному  присутствию  объекта  z;  «необходимо  z  и  возможно  z»  —  достоверному  отсутствии»  объекта  z;  «возможно  z  и  возможно  z»  —  неопределенности;  «необходимо  z  и  необходимо  z»  -  противоречию  и  т.  д.

Строгое  описание  взаимодействия  объектов  предметной  области  возможно  осуществить  в  рамках  формальных  теорий,  (такая  теория  состоит  из  множества  локальных  теорий,  каждая  из  которых  имеет  ограниченную  область  применения.  Опишем  формальные  теории  более  подробно.

В  исчислении  присутствия  объект  описывается  через  подобъекты  (существенные  признаки  объекта).  Для  формирования  теории  объекта  описание  через  подобъекты  замещается  морфизмами  в  данный  объект.  Совокупность  этих  морфизмов  образует  покрытие  объекта  U 

и  называется  решетом  над  объектом  U. 

Для  категории  К  можно  задать  семейство  решет  С(U),  по  одному  для  каждого  объекта  из  этой  категории,  т.  е.  объекты  U_I  могут  в  свою  очередь  иметь  покрытие  некоторым  семейством  морфизмов  φ_.  Так  как  композиции  морфизмов  также  образуют  покрывающее  семейство  для  U,  то  совокупность  таких  решет  для  категории  К  образует  так  называемую  топологию  Гротендика,  а  категория  вместе  с  такой  топологией  называется  сайтом  (местом).  Топология  Гротендика  определяется  для  так  называемых  малых  категорий,  морфизмы  (объекты)  которых  составляют  множества.  Каждому  морфизму  и  объекту  в  теории  ставятся  в  соответствие  классы  или  частные  примеры  конкретных  или  абстрактных  понятий  и  отношений  предметной  области.  Такое  определение  решета  равносильно  представлению  объектов  категории  U  представимыми  функторами,  т.  е.  множествами  морфизмов  Hom_k(U_i,U),  iI.

Представимые  функторы  составляют  основу  для  формирования  пучков  теорий  над  сайтом.  Это  позволяет  объединять  локальные  теории  отдельных  объектов  в  глобальную  теорию  реальности.  В  связи  с  тем,  что  каждая  категория  отражает  отдельный  аспект  знаний  о  предметной  области  (процессы,  состояния  и  т.  д.),  то  теория  объекта  T(Ob₁)  определяется  над  сайтом  из  произведения  категорий

T(Ob₁)  =  Kat₁  x  Kat₂  x  …  x  Kat_i  .

Динамика  поведения  объекта  в  физической  (абстрактной)  реальности  находит  свое  отражение  в  теории  объекта  через  изменение  оценок  присутствия  морфизмов,  связанных  с  данным  объектом.  С  этой  целью  вводится  понятие  дифференциала  присутствия  морфизма  (ДПМ).

Под  дифференциалом  присутствия  морфизма  понимается  синтаксическая  конструкция  вида 

принимающая  при  интерпретации  одно  из  двух  значений  —  S(ω,T_i),  N(ω,T_i)  и  означает  изменение  значения  присутствия  морфизма  с  α  на  β  в  результате  элементарного  шага  некоторого  процесса,  который  определяется  порядком  дифференциала  n.  При  этом  α  и  β  принимают  одно  из  значений  множества  констант  исчисления

,

где  Q  означает,  что  операция  по  определению  значения  присутствия  переменной  еще  не  выполнялась.  Можно  считать,  что  Q  выражает  полную  априорную  неопределенность  в  отличие  от  Un,  соответствующего  апостериорной  неопределенности,  то  есть  отсутствию  информации,  установленному  в  результате  анализа  имеющиеся  данных.

Порядок  ДПМ  n=1  описывает  состояние  реальности,  не  содержащее  изменений  морфизмов  (статика).  Если  изменение  является  результатом  шага  логического  вывода,  то  n=2.  При  n=3  изменение  присутствия  морфизма  получено  в  результате  изменения  теории  объекта.

Правила  построения  формул  теорий  объектов  можно  определить  на  основе  свойств  алгебры  дифференциалов  присутствия  морфизмов  с  операцией  композиции  .

При  необходимости  алгебра  ДПМ  может  быть  дополнена  операцией    альтернативного  присутствия.

В  общем  случае  аксиома  теории  может  быть  представлена  как  конъюнкция  по  присутствию  в  виде

где:    играют  роль  посылок  аксиомы,    роль  следствия.

Предложенный  подход  к  построению  модели  представления  знаний  позволяет  описывать  взаимодействие  различных  объектов  (программных  модулей,  неструктурированных  данных  и  др.)  через  входящие  и  исходящие  из  них  морфизмы,  строить  многоуровневые  иерархические  теории,  осуществлять  объединение  теорий  объектов  одного  уровня  с  другим  и  таким  образом  строить  глобальную  теорию  предметной  области,  что  обеспечивает  решение  задач  обработки  знаний  в  ГАИС,  осуществлять  интерпретацию  результатов  сложного  анализа  и  моделирования. 

Список  литературы:

1.Беспалов  А.П.  Умные  технологии  для  умного  управления.41-я  научно-практическая  конференция  «Современные  информационные  технологии  в  нефтяной  и  газовой  промышленности».  [Электронный  ресурс]  —  режим  доступа.  —  URL:  https://sites.google.com/site/41it2012/  (дата  обращения  10.07.13).

2.Богданов  Д.В.  Модели  и  алгоритмы  концептуального  проектирования  автоматизированных  систем  управления/  Под  ред.  С.Г.  Чекинова.  М.:  Компания  Спутник+,  2004.  —  324  с.

3.Болотник  Д.Н..  Технологии  интеллектуального  месторождения  и  некоторые  примеры  элементов  данной  технологии.  41-я  научно-практическая  конференция  «Современные  информационные  технологии  в  нефтяной  и  газовой  промышленности.  [Электронный  ресурс]  —  режим  доступа.  —  URL:  https://sites.google.com/site/41it2012/home/1/06  (дата  обращения  10.07.13). 

4. Ярушек  В.Е.  «Теоретические  основы  автоматизации  процессов  выработки  решений  в  системах  управления».  Харьков,  1993  г.,  —  443  с.