КОМПЬЮТЕРНОЕ  МОДЕЛИРОВАНИЕ  ТКАНИ

Ландовская  Ирина  Евгеньевна

аспирант  Новосибирского  государственного  технического  университета,  г.  Новосибирск

E-mail:  nairy@rambler.ru

Ландовский  Владимир  Владимирович

канд.  техн.  наук,  доцент  Новосибирского  государственного  технического  университета,  г.  Новосибирск

E-mail: 

COMPUTER  SIMULATION  OF  WOVEN  FABRICS

Landovskaya  Irina

postgraduate  student  of  Novosibirsk  State  Technical  University,  Novosibirsk

Landovsky  Vladimir

candidate  of  Science,  assistant  professor  of  Novosibirsk  State  Technical  University,  Novosibirsk

АННОТАЦИЯ

В  работе  рассматриваются  дискретная  модель  ткани  и  алгоритмы  для  моделирования  поведения  ткани  на  поверхности  твердого  многогранного  объекта  на  основе  метода  частиц  с  учетом  деформационных  свойств.  Предложено  описание  разработанного  метода  моделирования  соединительных  швов  при  сборке  изделий  из  нескольких  деталей.  Приведены  результаты  моделирования.

ABSTRACT

In  this  paper  a  discrete  model  of  fabric  and  algorithms  for  modeling  the  behavior  of  cloth  on  the  surface  of  multifaceted  solid  object  on  the  basis  of  particles  method  with  allowance  for  deformation  properties  are  considered.  There  is  a  description  of  developed  method  of  connecting  seams  simulation  in  the  assembly  of  products  from  multiple  parts.  The  simulation  results  are  presents.

Ключевые  слова:  моделирование  ткани;  метод  частиц;  физические  свойства  ткани;  моделирование  шва;  сборка  изделий  из  ткани.

Keywords:  simulation  fabric;  particles  method;  physical  properties  of  fabric;  simulation  seam;  assembly  of  products  from  fabric.

1.   Введение

Моделирование  поведения  ткани  при  драпировке  появилось  в  списке  компьютерных  приложений  сравнительно  недавно.  Одна  из  проблем  в  этой  области  связана  с  уникальностью  тканых  материалов.  Всегда  было  ясно,  что  тканые  материалы  имеют  свойства,  которые  позволяют  им  деформироваться  иначе,  чем  листам  других  материалов,  например,  бумаги  или  металлической  фольги.  Особые  возможности  деформации  ткани  были  отмечены  и  известны  всегда,  но  не  были  никогда  полностью  поняты  с  научной  или  инженерной  точки  зрения.

На  сегодняшний  день  существует  ряд  работ  посвященных  проблеме  моделирования  ткани  [2],  [5].  Однако,  до  сих  пор  не  предложен  способ  компьютерного  моделирования,  дающий  правдоподобные  результаты.  Также  в  работах  по  моделированию  ткани  не  уделяется  достаточного  внимания  соединительным  швам,  хотя  именно  их  поведение  во  многом  определяет  итоговый  результат  сборки.

2.     МОДЕЛИРОВАНИЕ  ТКАНИ

Основная  идея  заключается  в  том,  чтобы  рассматривать  ткань  как  систему  взаимодействующих  частиц  (узлов).  В  ткани  тонкие  волокна  скручены  в  нити,  и  эти  нити  более  или  менее  жестко  сплетены  во  взаимосвязанную  сеть.  Представим  модель  ткани  как  систему  частиц  [3],  которые  размещены  в  точках  пересечения  продольных  и  поперечных  нитей  ткани  (рис.  1).

Рисунок  1.  Дискретная  модель  ткани

Движение  системы  описывается  обобщенными  перемещениями:

,

и  на  каждом  временном  слое  ищутся  положения  узлов  в  пространстве.  Каждая  из  частиц  обладает  некоторой  массой,  находится  в  гравитационном  поле,  взаимодействует  с  окружающей  средой  и  соседними  частицами.  Тогда  уравнение  движения  частицы    имеет  следующий  вид:

,

где:    —  масса  частицы, 

  —  константа  демпфирования, 

составляющая    —  представляет  собой  потери  энергии  связанные  с  взаимодействием  частицы  с  окружающей  средой, 

  —  ускорение  свободного  падения.  Последняя  составляющая  уравнения  движения,  представляет  собой  результирующую  силу  взаимодействий  между  частицами, 

  —  множество  индексов  узлов  связанных  с  узлом  .

Обозначим  действие  внутренних  и  внешних  сил  на  ткань  ,  разрешив  уравнение  относительно  ,  получим  полную  систему  дифференциальных  уравнений    с  начальными  условиями:  ,  .  Введем  обозначение  .  И  перепишем  систему  уравнений  следующим  образом:

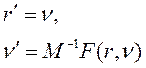
В  силу  того,  что  количество  частиц  как  правило  велико  и  каждое  дополнительное  вычисление  силы  требует  больших  временных  затрат  для  решения  системы  воспользуемся  схемой  с  перешагиванием:

Это  метод  второго  порядка  точности  и  в  сравнении  с  классическим  явным  методом  Эйлера  обладает  большей  устойчивостью,  позволяя  на  порядок  увеличить  шаг  интегрирования  [4].

3.   Деформационные  свойства  ткани

Основные  взаимодействия,  которые  происходят  на  уровне  нити,  это:  растяжение-сжатие,  изгиб  и  сдвиг.  Учитывая,  что  ткань  достаточна  легкая  и  вес  ткани  в  удаленных  узлах  оказывает  пренебрежимо  малое  влияние  на  каждую  рассматриваемую  частицу,  предположим,  что  на  каждую  внутреннюю  частицу  влияют  12  соседних  частиц.  На  рис.  2  взаимодействия  растяжения-сжатия,  сдвига  и  изгиба  обозначены  связями  1,  2  и  3  соответственно.

Рисунок  2.  Типы  деформируемых  ребер

Силу  растяжения-сжатия  будем  вычислять  как:

,

где:    —  линейный  коэффициент  растяжения-сжатия, 

  —  расстояние  между  частицами, 

  —  расстояние  между  частицами  в  состоянии  покоя,  рис.  3a.

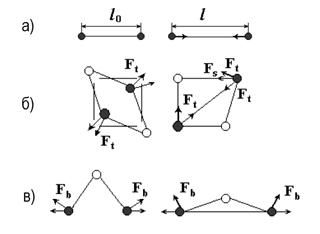
Рисунок  3.  Взаимодействие  частиц

Моделирования  взаимодействий  изгиба  и  сдвига  представим  через  растяжение-сжатие.  В  этом  случае  взаимодействие  сдвига  заменим  растяжением-сжатием  частиц  образующих  диагональ  ячейки  (рис.  3б),  а  в  случае  изгиба  введем  дополнительные  взаимодействия  отталкивания  через  узел  (рис.  3в).

Таким  образом,  можно  рассчитать  внутреннюю  силу,  с  которой  частица    воздействует  на  частицу  :

,

где:    коэффициент  жесткости  связи  между    и  , 

  —  вектор  взаимодействия  между    (начало  вектора)  и    (конец  вектора), 

  —  расстояние  между  частицами,  когда  внутренние  силы  равны  нулю  (ткань  находится  в  покое).

4.   Моделирование  соединительных  швов

При  моделировании  сборки  трехмерных  объектов  из  плоских  заготовок  почти  всегда  возникает  необходимость  моделирования  швов  при  соединении  деталей  друг  с  другом.  Тут  возникает  несколько  проблем:  во-первых  —  передача  характеристик  шва,  таких  как  жесткость,  растяжение  и  прочее,  к  тому  же  сами  характеристики  шва  отличаются  от  характеристик  ткани.  Во-вторых  —  процесс  осложняется  тем,  что,  как  правило,  в  местах  соединения,  у  деталей  оказывается  разное  количество  частиц,  что  не  позволяет  применять  методы,  используемые  при  моделировании  целостной  ткани.

Для  того,  чтобы  произвести  сборку  изделия,  сначала  надо  соединить  детали  вместе,  т.  е.  «сшить»  их,  и  лишь  потом,  используя  внешние  силы  окончательно  завершить  моделирование. 

При  создании  шва  учитываются  расположения  частиц  двух  «сшиваемы»  деталей.  По  ширине  шов  состоит  из  3  частиц,  это  требуется  для  того,  чтобы  смоделировать  параметры  шва,  такие  как  растяжение-сжатие,  изгиб  и  сдвиг,  что  влияет,  главным  образом,  на  «жесткость»  шва.  Частицы  шва  расположены  так,  что  в  начальном  состоянии  соответствуют  расположению  крайних  частиц  деталей  на  «сшиваемых»  сторонах  (находятся  «напротив»  крайних  частиц  ткани).  Т.  е.  в  случае,  если  сшиваемы  детали  по  линии  соединения  не  содержат  «совпадающих»  частиц,  то  шов  по  длине  будет  состоять  из    частиц,  где    —  количество  частиц  на  линии  соединения  первой  детали,  а    —  количество  частиц  на  линии  соединения  второй  детали  (рис.  4).

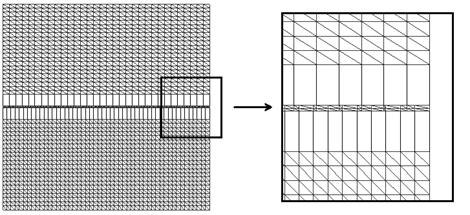
Рисунок  4.  Модель  до  начала  «сшивания»

Затем  указывается,  какие  частицы  должны  быть  соединены  между  собой,  и  начинается  первый  этап  сборки.  Так  как  расстояния  между  частицами  шва  различны,  то  во  время  вычисления  используется  нормирующий  коэффициент,  чтобы  обеспечить  одинаковое  воздействие  сил  на  частицы  шва.  Во  время  моделирования  «сшивания»  внешние  силы  не  применяются,  а  учитывается  только  взаимодействие  с  объектом.  Шьющие  силы  применяются  только  к  частицам,  находящимся  на  границах  деталей  и  шва,  что  гарантирует,  соединения  двух  деталей  изделия  в  одну  по  линии  шва  (рис.  5). 

Рисунок  5.  «Сшитая»  модель

Когда  границы,  которые  должны  быть  сшиты,  находятся  во  взаимном  контакте,  начинается  второй  этап  моделирования,  где  происходит  воздействие  внешних  сил  на  ткань,  и  также  продолжается  проверка  на  столкновение  с  объектом  [1].  Результаты  моделирования  представлены  в  пункте  5.

5.   результаты  моделирования

Ниже  представлены  результаты  сборки,  полученные  с  использованием  компьютерной  программы  моделирования  ткани,  доказывающие  эффективность  предложенного  алгоритма.  На  рисунке  6  показаны  исходная  модель  ткани,  состоящая  из  двух  «сшиваемых»  деталей  и  соединительного  шва  (слева),  и  объект,  на  поверхности  которого  производилась  сборка  (справа).

Рисунок  6.  Исходная  модель

Результаты  сборки  отображены  на  рис.  7.  На  рис.  7а  показана  проекция  на  плоскость  XY  (вид  сверху),  рис.  7б  —  проекция  на  плоскость  XZ  (вид  сзади),  рис.  7в  —  проекция  на  плоскость  YZ  (вид  сбоку).

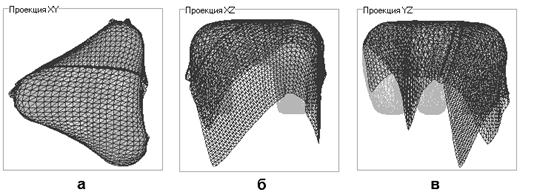
Рисунок  7.  Результаты  сборки

Отображение  результатов  моделирования,  представленное  на  рис.  8,  получено  экспортом  данных  в  программу  трехмерного  моделирования  Rhinoceros.

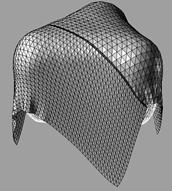
Рисунок  8.  Результаты  моделирования

Полученные  результаты  показали  эффективность  выбранного  подхода  моделирования  соединительных  швов  ткани,  и  возможность  успешно  использовать  такой  метод  для  моделирования  сборки  тканых  изделий  из  деталей.

Список  литературы:

1.Ландовский  В.В.  Моделирование  взаимодействий  ткани  с  твердыми  многогранными  объектами  //  Сборник  научных  трудов  НГТУ,  —  2006.  —  №  2(44).  —  с.  53—58.

2.Baraff  D.  and  Witkin  A.  Large  steps  in  cloth  simulation.  In  SIGGRAPH  98  Conference  Proceedings,  Annual  Conference  Series,  pages  43—54.  ACM  SIGGRAPH,  1998.

3.Hockney  W.,  Eastwood  J.  Computer  Simulation  Using  Particles.  McGraw-Hill,  New  York,  1981.

4.Landovsky  V.  Integration  methods  in  the  problem  of  modelling  of  fabric  based  on  particles  method.  Proc./15th  International  Conference  on  Computer  Graphics  and  Applications.  Novosibirsk,  2005.  p.  234—241.

5.Provot  X.  Deformation  constraints  in  a  mass-spring  model  to  describe  rigid  cloth  behavior.  In  Graphics  Interface,  —  pages  147—155,  —  1995.