ИСПОЛЬЗОВАНИЕ  ОБОБЩЕННЫХ  ГАУССОВЫХ  ЧИСЕЛ  ПРИ  РАСЧЕТЕ  ГЕРТ-СЕТИ

Черменев  Дмитрий  Александрович

аспирант,  Воронежский  Государственный  Технический  Университет,  г.  Воронеж

E-mail: 

USING  GENERALIZED  GAUSSIAN  INTEGERS  IN  CALCULATING  GERT  NETWORK

Chermenev  Dmitriy  Aleksandrovich

postgraduate,  Voronezh  State  Technical  University,  Voronezh

АННОТАЦИЯ

В  статье  рассматривается  подход  к  расчету  ГЕРТ  сети,  когда  продолжительности  работ  задаются  в  форме  обобщенных  гауссовых  чисел,  содержащих  ряд  параметров,  которые  позволяют  настроить  информационную  среду  задачи  на  конкретного  пользователя.

ABSTRACT

The  paper  discusses  an  approach  to  the  calculation  of  GERT  network  when  the  duration  of  the  work  are  given  in  the  form  of  generalized  Gaussian  numbers  containing  the  number  of  options  that  allow  you  to  customize  the  information  environment  of  the  problem  to  a  specific  user.

Ключевые  слова:  нечеткое  гауссово  число,  Герт  сеть

Keywords:  Gaussian  fuzzy  number,  GERT  Network

Многие  проекты  не  могут  быть  адекватно  описаны  в  терминах  ограничений,  накладываемых  на  классические  сетевые  графики.  Были  разработаны  обобщенные  сетевые  графики,  также  называемые  ГЕРТ  сетью,  для  которых  данные  ограничения  не  вводятся.

Рассмотрим  сеть  ,  содержащую  только  ГЕРТ-узлы  (Рис.  1),  которые  образуют  множество  .

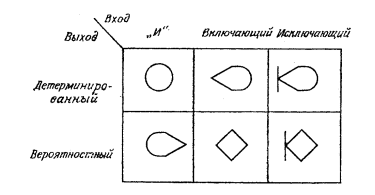
Рисунок  1.  ГЕРТ-узлы

В  [1,  с.  389]  время  выполнения  операции    есть  случайная  величина.  По  определению  операция    может  быть  выполнена  только  в  том  случае,  если  выполнен  узел  .

Пусть    —  условная  вероятность  или  плотность  распределения  времени  выполнения  операции  .  Условная  производящая  функция  моментов  случайной  величины    определяется  как  ,  т.  е. 

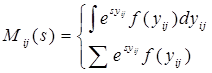                                   (1)

В  частности,    при.  Если,  то  .

Пусть—  вероятность  того,  что  операция    будет  выполнена  при  условии,  что  узел    выполнен.  Для  случайной  величины    -функция  определяется  как

                                               (2)

Для  последовательных  ветвей  -функция  примет  вид:

                            (3)

Для  параллельных  ветвей  соответственно  получаем  результат:

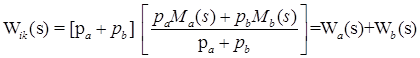                     (4)

Для  циклической  ветви  имеем  следующее  выражение:

                                   (5)

Однако  время  выполнения  работ  в  большинстве  случаев  не  является  случайной  величиной,  т.  е.  имеет  место  неопределенность,  а  не  случайность.

Для  времени  выполнения  операции    предлагается  использовать  обобщенные  Гауссовы  числа  (L-R)-типа  с  функцией  принадлежности  вида:

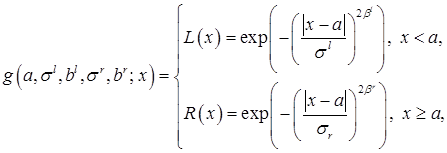                         (6)

где:    —  модальное  значение, 

  —  параметры  формы  для  функций    и    соответственно, 

  —  параметры  «ширины»  нечеткого  числа  соответственно  слева  и  справа  от  модального  значения. 

Так  как  функция  принадлежности  является  выпуклой,  то  -срез  представляет  собой  интервал  или  отрезок  в  зависимости  от  того  является  он  строгим  или  слабым.  В  дальнейших  рассуждениях  будем  использовать  слабые  -срезы,  границы  которых  определяются  следующим  образом:

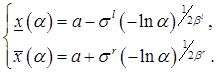
Обозначив  ,  получим

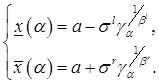                                                       (7)

Для  -среза  можно  вычислить  среднее  значение 

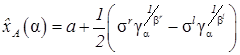                                      (8)

Данное  значение  реализует  функцию  дефаззификации.

Полученное  значение  будем  использовать  в  качестве  времени  выполнения    при  расчете  ГЕРТ-сети.  Тогда 

                (9)

Топологическое  уравнения  для  замкнутых  графов,  известное  как  правило  Мейсона,  имеет  следующий  вид:

           (10)

Расчет  ГЕРТ  сети  производится  по  следующему  алгоритму:

1.  Замкнуть  сеть  дугой,  ведущей  из  конечного  узла  в  начальный.

2.  Найти  все  петли  порядка  n.

3.  С  помощью  топологического  уравнения  (9)  получить  выражение  для 

Рассмотрим  следующую  ГЕРТ  сеть.

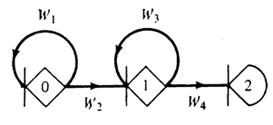
Рисунок  2.  Пример  ГЕРТ  сети

Пусть  время  выполнения  всех  операций  задано  в  виде  обобщенных  Гауссовых  чисел  с  параметрами,  представленными  в  табл.  1.

Таблица  1. 

Значения  параметров  функции  принадлежности  продолжительностей  работ  и  вероятность  их  выполнения

Замкнем  исходную  сеть  дугой  исходящей  из  конечного  узла  и  входящую  в  исходный  узел,  Получим  сеть  изображенную  на  рис.  2.

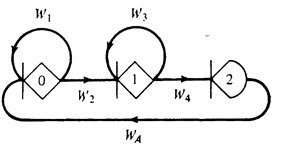
Рисунок  3.  ГЕРТ  сеть  с  замкнутым  контуром

Топологическое  уравнение  примет  следующий  вид:

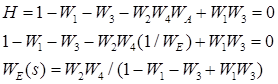
Используя  выражения  (2)  и  (8),  полагая,  что  ,получаем:

Окончательно:

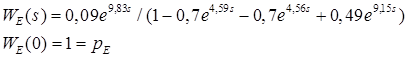
Отсюда  следует,  что 

Вычислим  первую  производную:

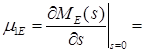31,18

Полученное  число  является  математическим  ожиданием  времени  выполнения  сети.

Таким  образом  в  статье  рассмотрена  ГЕРТ  сеть  с  временами  работ  в  виде  обобщенного  Гауссова  нечеткого  числа.  При  использовании  нечетких  чисел  можно  получить  различные  результаты  в  зависимости  от  настройки  различных  параметров,  что  дает  большую  гибкость  при  выборе  метода  расчета.

Список  литературы:

1.Филлипс  Д.,  Гарсиа-Диас  А.  Методы  анализа  сетей  /  Д.  Филлипс,  А.  Гарсиа-Диас.  М.:  Мир,  1984.  —  496  с.