Статья опубликована в рамках: XXII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 15 июля 2013 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОД РЕШЕНИЯ УРАВНЕНИЙ ТЕПЛОПРОВОДНОСТИ
Кошлак Анна Владимировна
канд. техн. наук, кафедра теплогазоснабжения, вентиляции и теплоэнергетики, доцент Полтавского национального технического университета имени Юрия Кондратюка, г. Полтава
E-mail: am.pavlenko@yandex.ua
Павленко Анатолий Михайлович
д-р техн. наук, зав. кафедрой теплогазоснабжения, вентиляции и теплоэнергетики, профессор Полтавского национального технического университета имени Юрия Кондратюка, г. Полтава
E-mail:
Усенко Богдан Олегович
аспирант кафедры теплогазоснабжения, вентиляции и теплоэнергетики, ассистент Полтавского национального технического университета имени Юрия Кондратюка, г. Полтава
E-mail:
THE METHOD SOLVING THE THERMAL CONDUCTIVITY EQUATION
Koshlak Anna
candidate of Science, heat and gas supply, ventilation and heat power engineering department, associate professor of Poltava National Technical Yuri Kondratyuk University, Poltava
Pavlenko Anatoly
doctor of Science, Head of heat and gas supply, ventilation and heat power engineering department, professor of Poltava National Technical Yuri Kondratyuk University, Poltava
Usenko Bogdan
postgraduate of heat and gas supply, ventilation and heat power engineering department, assistant of Poltava National Technical Yuri Kondratyuk University, Poltava
АННОТАЦИЯ
В статье предложена методика решения линейных дифференциальных уравнений второго порядка, часто встречающихся в задачах математической физики, в частности в задачах теплопроводности.
ABSTRACT
In the article proposed a method for solving linear differential equations of second order commonly encountered in problems of mathematical physics, in particular in heat transfer problems.
Ключевые слова: теплопроводность, методика расчёта теплопроводности, тепломассообмен
Keywords: thermal conductivity, thermal conductivity calculation method, heat and mass transfer
В работе [1, с. 48] предложена методика решения задач теплопроводности многослойной частицы, суть которой заключалась в сведении параболических уравнений к обыкновенному дифференциальному уравнению.
Настоящая работа является развитием данной методики.
Постановка задачи. Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка
![]() (1)
(1)
где: р(х) и g(х) — непрерывные функции в интервале (а; в);
y(х) — искомая функция. Известно, что
![]() ,(2)
,(2)
где: y1(х), y2(х) — фундаментальная система решений уравнения (1), а вронскиан этой системы функций
![]() (3)
(3)
Если ЛОДУ имеет постоянные коэффициенты, то его решение сводится к квадратному алгебраическому уравнению.
В задачах теплопроводности постоянные коэффициенты уравнений встречаются не часто, и, скорее всего в упрощенных случаях рассмотрения физического процесса. Поэтому в данной работе поставлена цель усовершенствования предложенной ранее методики [1, 2].
В настоящей работе предлагается алгоритм, позволяющий уравнение (1) сводить к квадратному алгебраическому уравнению с переменными коэффициентами. Для этого введем вспомогательную функцию ![]() , которая связана с решением y(х) и коэффициентами р(х) и g(х) и может принимать различные выражения. Рассмотрим несколько вариантов функции
, которая связана с решением y(х) и коэффициентами р(х) и g(х) и может принимать различные выражения. Рассмотрим несколько вариантов функции ![]() .
.
І. Пусть 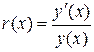 , тога
, тога 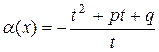 или
или ![]() , (4)
, (4)
где
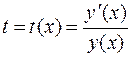 . (5)
. (5)
Уравнение (4) — квадратное алгебраическое уравнение относительно t, решая которое, имеем
![]()
и учитывая (5)
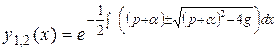 (6)
(6)
На функцию α(х) необходимо наложить условие
![]() , или
, или
![]() ,(7)
,(7)
которое можно записать в виде
![]() (8)
(8)
При этом α(х) – произвольная функция, и ее можно выбрать следующим образом
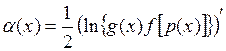 .(9)
.(9)
Подставляя функцию (9) в условия (8) придем к дифференциальному уравнению Бернулли
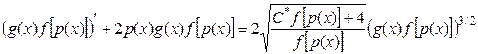 , (10)
, (10)
решая которое, получим
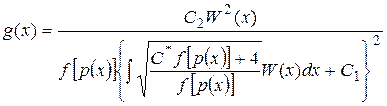 . (11)
. (11)
В частности, если ![]() =1, то
=1, то
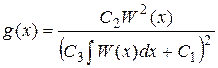 .(11а)
.(11а)
Из курса дифференциальных уравнений известно, что ЛОДУ (1) можно привести к уравнению с постоянными коэффициентами при помощи замены независимой переменной
![]() , (12)
, (12)
а учитывая (11)
![]() (13)
(13)
ІІ. Выберем в качестве
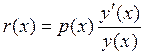 ,
, 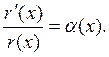 (14)
(14)
В этом случае
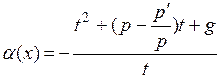
Или
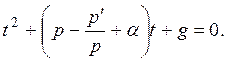 (15)
(15)
Корни этого квадратного уравнения
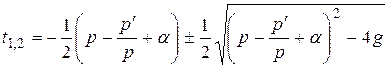 (16)
(16)
и фундаментальная система решений ЛОДУ (1)
![]() ;
; ![]() .
.
На функцию α(х) необходимо наложить условие
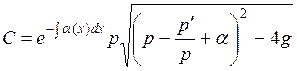 ; (17)
; (17)
или
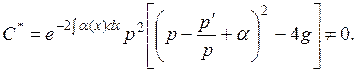 (18)
(18)
В качестве α(х) можно выбрать
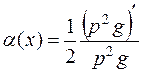 . (19)
. (19)
И условие (18) запишем в виде дифференциального уравнения Бернулли
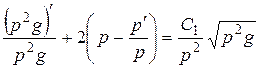 , (20)
, (20)
решая которое относительно g(х)
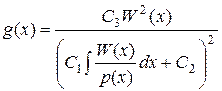 . (21)
. (21)
ІІІ. Представим r(х) в виде
 , (22)
, (22)
или что равносильно
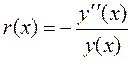 . (23)
. (23)
Квадратное алгебраическое уравнение в этом случае имеет вид
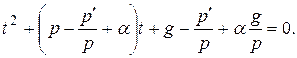 (24)
(24)
Корни уравнения (24)
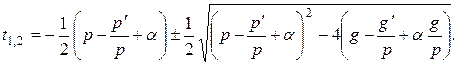 (25)
(25)
При этом уравнение, связывающее функции α(х), р(х) и g(х), следующее
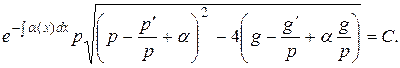 (26)
(26)
В этом случае мы имеем больше вариантов условий на функцию α(х).
а) 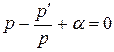 ,
, 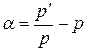 . (27)
. (27)
Подставляя (27) в уравнение (26), получим  , которое является линейным относительно g(х), и решая которое имеем
, которое является линейным относительно g(х), и решая которое имеем
![]() (28)
(28)
б) 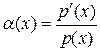 ,
, 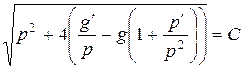 ,
,
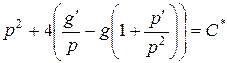 ; (29)
; (29)
Решая линейное уравнение (29), получим
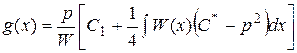 . (30)
. (30)
с) ![]() (31)
(31)
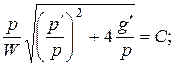
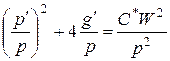 ;
;
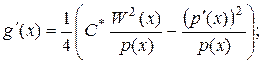 (31)
(31)
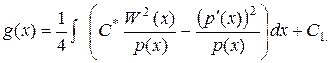 (32)
(32)
ІV. Можно представить![]() r(х) в виде
r(х) в виде
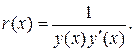 (33)
(33)
Квадратное уравнение в этом случае
![]() (34)
(34)
и его решение
![]() (35)
(35)
Уравнение, связывающее функции α(х), р(х) и g(х) в этом случае
![]()
Или
![]() (36)
(36)
Задавая определенные выражения для α(х), мы будем получать конкретные дифференциальные или трансцендентные уравнения.
Рассмотрим сведение ЛОДУ (1) к интегро-дифференциальным уравнениям. Для этого уравнение (1) запишем в виде
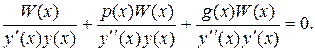 (37)
(37)
Дифференцируя каждое слагаемое уравнения (37), и учитывая уравнение (1) и его производную, а затем, интегрируя, получим
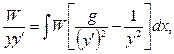
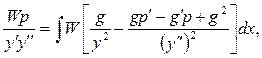 (38)
(38)
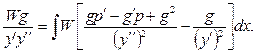
Если ввести обозначения
![]()
![]()
![]()
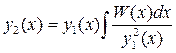 ,
, 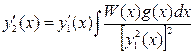 ,
, 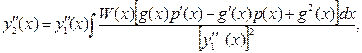
то получим хорошо известные формулы
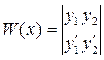 ;
; 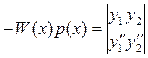 ;
; 
Результаты расчета
Рассмотрим решение задачи тепломассообмена влажной частицы в потоке теплоносителя со следующими условиями:
·концентрация пара базовой жидкости изменяется от максимального значения у поверхности частицы до постоянной величины, определяющей влажность окружающей среды, начиная с ri;
·аналитическое исследование градиента концентрации пара выполнено в области LÎ[R...R2], причем R2 >> ri;
·распределение температуры внутри частицы определено с учетом понижения температуры поверхности за счет испарения жидкости.
Процесс ТМО частицы ЭТС в условиях свободной конвенции имеет некоторые отличительные особенности, учет которых усложняет решение задачи, но максимально приближает его к физическому процессу. Глобулы частицы представляют собой источник энергии, поэтому для данной зоны уравнение теплопроводности запишем в виде
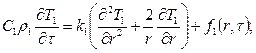 r
r![]() (39) для оболочки
(39) для оболочки
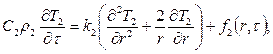 (40)
(40)
![]()
За счет испарения температура поверхности кластера снижается
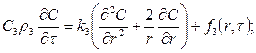 (41)
(41)
![]()
В точке сопряжения на радиксе R1 контакт не идеальный, т. е.
![]()
![]() (42)
(42)
Для поверхности R2 условие сопряжения запишем в виде
![]()
![]() (43)
(43)
Таким образом, система уравнений, описывающая данный процесс выглядит следующим образом:
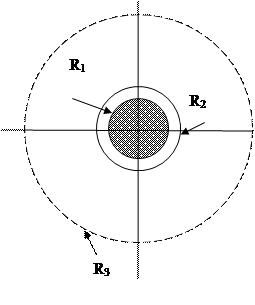
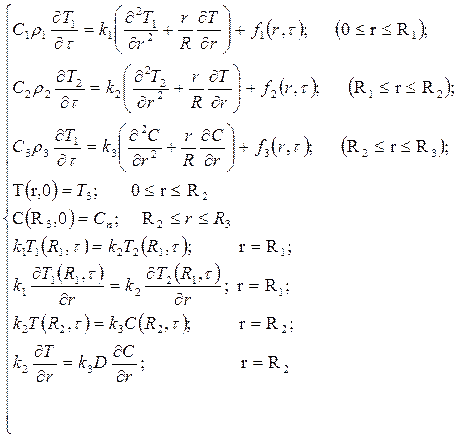
Вначале рассмотрим условие
![]() (44)
(44)
Решение представим в виде
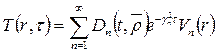 (45)
(45)
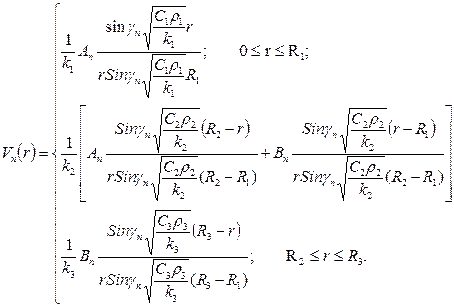 .
.
При выборе ![]() удовлетворяются граничные условия (42), (43). Удовлетворим условиям (42), (43) для этого получим систему линейных алгебраических уравнений
удовлетворяются граничные условия (42), (43). Удовлетворим условиям (42), (43) для этого получим систему линейных алгебраических уравнений
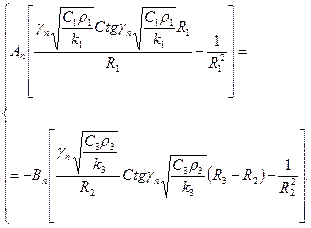 (46)
(46)
Система (46) будет иметь ненулевое решение, если главный определитель этой системы равен нулю
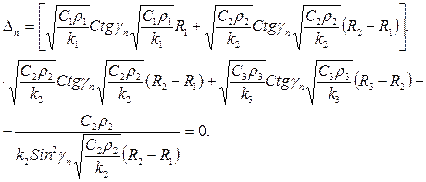 (47)
(47)
Из уравнения (47) определяются собственные числа ![]() .
.
Но тогда
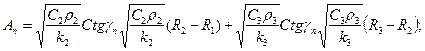
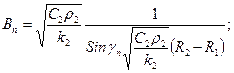 (48)
(48)
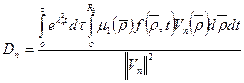 (49)
(49)
Где
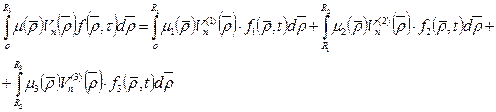
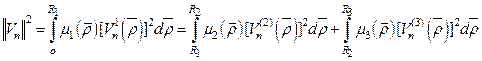 (50)
(50)
На рис. 1 показаны зависимости, отражающие физический процесс теплопередачи, полученные эмпирическим, полуэмпирическим и аналитическим путем. Из рисунка следует, что разработанные аналитический и полуэмпирический методы расчета с достаточной точностью описывают реальный процесс.
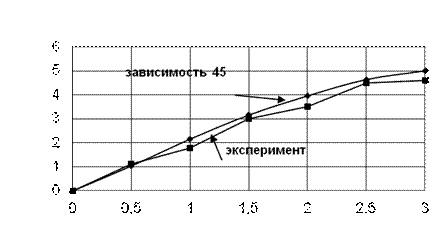
Рисунок 1. Понижение температуры поверхности влажной частицы диаметром 2 мм. за время τ.
Выводы:
1. Вариантов выбора функции r(х) можно предложить более десяти.
2. Предложенную методику можно успешно использовать при решении уравнения Риккати и систем двух линейных однородных дифференциальных уравнений первого порядка.
3. Незначительно видоизменив предложенную методику можно найти решения ЛОДУ третьего и четвертого порядков.
Список литературы:
1.Павленко А.М., Давыдов И.А., Кошлак А.В. Нестационарная теплопроводность слоистых тел// Математичні проблеми технічної механіки, 2003. — 48—52 с.
2.Павленко А.М./ Тепломассообмен частицы в потоке теплоносителя// Павленко А.М., Давыдов И.А., Кошлак А.В. — Дн-к: ДГТУ, 2009. —140 с.
дипломов


Оставить комментарий