АНАЛИЗ  ТЕХНОЛОГИЧЕСКОГО  ПРОЦЕССА  ВЫТЯЖКИ  ОПТИЧЕСКИХ  СТЕРЖНЕЙ С  ПОМОЩЬЮ  МАТЕМАТИЧЕСКИХ  МОДЕЛЕЙ

Алексеева  Любовь  Борисовна

Доцент,  канд.  техн.  наук,  доцент  кафедры  машиностроения,  Национальный  минерально-сырьевой  университет  «Горный»,  г.  Санкт-Петербург

E-mali:  lbalek@rambler.ru

PROCESS  ANALYSIS  OF  OPTICAL  RODS EXTRACTION  USING  MATHEMATICAL  MODELS

Lubov  Alekseeva 

PhD  in  Engineering  Sciences,  Associate  professor  of  mechanic  engineering  department,  National  University  of  mineral  resources  “Mountain”,  St.Petersburg 

АННОТАЦИЯ

Процесс  вытяжки  стеклоизделий  из  разогретой  стекломассы  рассматривается  как  объект  управления,  свойства  которого  опреде­ляются  на  основе  интегрирования  системы  нелинейных  дифференци­альных  уравнений  в  частных  производных.

ABSTRACT

The  process  of  glassware  extraction  from  the  heated  fluid  glass  is  considered  as  a  controlled  element  whose  properties  are  determined  on  basis  of  integrating  the  system  of  nonlinear  differential  equations  in  partial  derivatives. 

Ключевые  слова:  объект  управления;  стекломасса;  математическая  модель;  устойчивость  движения;  зона  формирования.

Key  words:  controlled  element;  fluid  glass;  mathematical  model;  stability  of  motion;  formation  zone.

Объект  исследования  —  технологический  процесс  вытягивания  оптических  стержней  из  размягченной  стекломассы.  Для  каждого  типа  изделий  необходима  своя  специфическая  технология  производства.  Но  во  всех  технологических  процессах  неизменно  присутствует  операция  изготовления  одножильных  стержней  (световодов).  Это  могут  быть  полые  трубки,  тонкие  штабики  с  диаметром  поперечного  сечения  0,5…2  мм.  При  их  изготовлении  применяется  метод  вытягивания  размягченной  стекломассы  через  фильеру  или  метод  перетягивания  из  заготовки,  конец  которой  размягчен  в  печи  нагрева. 

Потребность  развития  автоматизированного  управления  произ­водством  световодов  приводит  к  необходимости  изучения  технологи­ческого  процесса  как  объекта  управления,  позволяющего  идентифи­цировать  скрытую  динамику  протекающих  процессов.  Это  повышает  полноту  и  достоверность  информационного  обеспечения  автоматизи­рованного  управления  технологическим  процессом  вытяжки. 

Управляемость  процесса  вытяжки  определяется  во  многом  как  физическим  состоянием  стекломассы,  так  и  кинематическими  и  динамическими  параметрами  устройств  вытяжки:  равномерностью  скоростей  подачи  и  вытяжки,  уровнем  виброактивности  подвижных  частей  технологического  оборудования,  инерционностью  переходных  режимов,  обусловленных  необходимостью  корректировки  параметров  процесса.  На  рисунке  1  приведена  структура  проводимых  исследований.

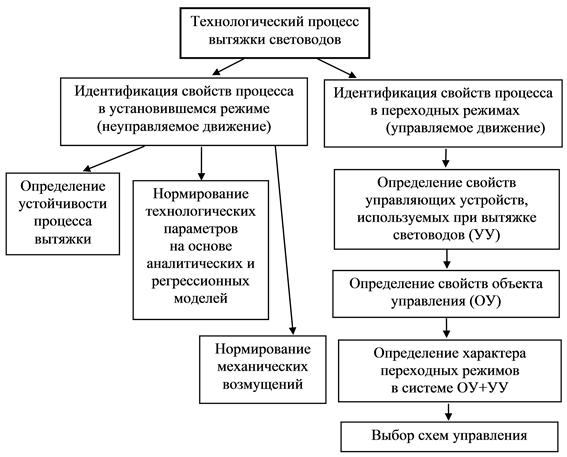
Рисунок  1.  Структура  проводимых  исследований

Процесс  образования  геометрии  стержня  происходит  в  зоне  формирования,  которая  представляет  собой  переход  от  разогретой  стекломассы  к  готовому  стержню.  Зона  формирования  —  тело  вращения.  Поэтому  для  составления  уравнений  движения  применялась  цилиндрическая  система  координат:  z  —  осевая,  r  —  радиальная  координаты.  Рассматривалась  одномерная  модель,  для  которой  скорость,  вязкость,  напряжение  являются  функциями  времени  и  осевой  координаты.  В  этом  случае  система  разрешающих  уравнений  сводится  к  трем  уравнениям:  неразрывности,  равновесия  сил,  физическое,  описывающее  состояние  стекломассы  [1,  с.  840].  В  работе  использовались  модели  вязкой  (ньютоновской)  жидкости  и  вязко­упругой  релаксирующей  среды  (модель  Максвелла)  [2,  с.  175].

Вязкая  и  вязкоупругая  среды  описываются  уравнением 

,

где:  ,  ,    —  соответственно  время,  скорость  и  напряжение  в  рассматриваемом  сечении  зоны  формирования; 

  —  динамическая  вязкость  среды; 

  —  время  релаксации; 

  —  модуль  упругости  стекломассы.

На  первом  этапе  исследуется  устойчивость  движения  стекло­массы  в  зоне  формирования.  Процесс  вытяжки  считается  устойчивым,  если  при  малых  неконтролирумых  возмущениях  зона  формирования  сохраняет  свою  первоначальную  форму.  Анализ  показал,  что  зона  формирования,  обладающая  только  вязкими  свойствами  ,  неустойчива.  Для  модели  вязкоупругой  среды  найдена  область  технологических  параметров  (скорость  вытяжки  ,  вязкость  ),  в  которых  система  устойчива.  Эта  область  определяется  неравенством  ,  где    —  длина  зоны  формирования.  Следовательно,  с  увеличением  вязкости  стекломассы  и  скорости  вытяжки  запас  устой­чивости  возрастает.  Это  подтверждается  результатами  экспериментов. 

Потеря  устойчивости  при  нулевом  времени  релаксации  объясняется  тем,  что  приведенное  уравнение  сводится  к  закону  Ньтона,  соответствующему  мгновенному  следованию  напряжения  за  скоростью  деформации.  Следовательно,  скорость  распространения  возмущений  бесконечна.

У  вязкоупругих  сред  скорость  распространения  возмущений  конечна.  Это  связано  с  явлением,  которое  называют  «предисторией»  потока  [1,  с.  840]. 

Полученные  результаты  позволяют  сделать  качественные  выводы.  Например,  для  получения  более  точной  геометрии  световодов  необходимо,  чтобы  стекломасса  в  зоне  формирования  обладала  свойствами  вязкоупругого  тела.  Такого  состояния  она  может  достичь  при  снижении  температуры  в  зоне  формирования.  Это  предопределяет  выбор  метода  изготовления  световодов  из  заготовки.  При  исполь­зовании  фильерного  метода  необходимо  создавать  особые  условия  для  прохождения  вязкоупругой  стекломассы  через  фильеры.

При  исследовании  переходных  процессов,  возникающих  при  управлении,  надо  учитывать  как  свойства  объекта  управления,  так  и  исполнительных  устройств.  Для  описания  этих  процессов  используется  система  линейных  дифференциальных  уравнений.  Исполнительное  устройство  формирует  возмущающую  силу,  дейст­вующую  на  объект  управления.  Для  воздействия  произвольного  вида,  прикладываемого  к  объекту  управления  в  начальный  момент  времени,  переходный  процесс  определен  на  основе  интеграла  Дюамеля-Карсона.  Реакция  объекта  управления  на  единичный  импульс  зависит  от  вязкоупругих  свойств  стекломассы.

Параметры  исполнительного  устройства  оказывают  основное  влияние  на  вид  переходных  процессов.  Параметры  зоны  формиро­вания  (объекта  управления)  влияют  на  время  переходного  процесса,  которое  определяет  качество  управления.

Характер  переходного  процесса  позволяет  выбрать  способ  управ­лении.  Если  переходный  процесс  происходит  без  перерегулирования,  то  целесообразно  выбрать  форсированное  управление.  Если  переход-ный  процесс  имеет  колебательный  характер,  то  для  уменьшения  его  времени  можно  ввести  квазиоптимальное  управление.

Список  литературы:

1. Лойцянский Л.Г. Механика жидкости и газа:  учеб.пособие. — М.: Гл. ред. физ.-мат. лит., 1987. — 840  с.

2. Уваров В.П., Алексеева Л.Б.  Нормирование  управляющих  факторов  процесса  вытяжки  световодов  с  помощью  аналитических  и  регресионных  моделей  //  Проблемы  машиноведения  и  машиностроения:  межвуз.  сб.  Вып.  37.  —  СПб.:  СЗТУ,  2007.  —  С.  175—178.