ИССЛЕДОВАНИЕ  УДАРНЫХ  ПОЛЯР,  ОПИСЫВАЮЩИХ  КОСЫЕ  СКАЧКИ  УПЛОТНЕНИЯ

Упырев  Владимир  Владимирович

инженер  лаборатории  «НМиНКБС_СВЧ_ЭиМ», 
Федеральное  государственное  бюджетное  образовательное  учреждение  высшего  профессионального  образования  Санкт-Петербургский  национальный  исследовательский  университет  информационных  технологий,  механики  и  оптики,

РФ,  г.  Санкт-Петербург,

Е- mail:  upyrevvv@ya.ru

 

OBLIQUE  COMPRESSION  SHOCK  WAVE  AND  SHOCK  WAVE  POLARS

Vladimir  Upyrev

Engineer  of  laboratory  «NMiNKBS_SVCh_JeiM», 
Saint-Petersburg  National  Research  University  of  Information  Technologies,  Mechanics  and  Optics,

Russia ,  Saint-Petersburg,

 

АННОТАЦИЯ

Рассматривается  история  изучения  условий  динамической  совместности  на  косом  скачке  уплотнения,  определяющих  соотношение  значений  газодинамических  переменных  до  разрыва  и  сразу  за  ним.  Приведена  математическая  модель  косого  скачка  уплотнения.  Вводится  понятие  ударной  поляры.  Выполнено  исследование  свойств  ударных  поляр.  Уделено  внимание  особым  точкам  на  ударных  полярах  и  их  значению  для  исследования  свойств  скачков  и  их  интерференции.  Исследования  выполнены  при  финансовой  поддержке  Министерства  образования  и  науки  РФ  (Соглашение  №  14.575.21.0057).

ABSTRACT

In  this  work  we  review  history  of  research  on  conditions  of  dynamic  compatibility  conditions  on  the  oblique  shock  wave  defining  value  relation  of  gas-dynamic  variable  before  and  right  after  discontinuity.  Mathematical  model  for  an  oblique  shock  wave  is  presented.  A  shock  waves  polar  term  was  introduced.  Conducted  research  of  shock  wave  polar’s  properties.  Attention  to  special  points  on  shock  wave  polars  and  their  value  for  research  of  shock  wave  properties  and  interference  is  paid.  The  researches  are  executed  with  the  financial  support  of  the  Ministry  of  Education  and  Science  of  the  Russian  Federation  (the  Agreement  №  14.575.21.0057).

 

Ключевые  слова :  косой  скачок  уплотнения;  газодинамический  разрыв;  условия  динамической  совместности;  ударная  поляра

Keywords :  obliques  compression  shock  wave;  gaz-dynamic  discontinuity;  gaz-dynamic  compatibility  conditions;  shock  wave  polar.

 

ВВЕДЕНИЕ

Цель  —  привести  основные  соотношения  на  косом  скачке  уплотнения  в  универсальной  форме,  которую  можно  применять  и  для  случая  изоэнтропических  волн,  исследовать  свойства  зависимостей  газодинамических  переменных  за  скачком  от  параметров  течения  перед  ним,  продемонстрировать  графический  метод  решения  задач  об  интерференции  газодинамических  разрывов,  привести  для  этих  задач  необходимый  графический  материал.  Основные  понятия  о  газодинамическом  разрыве  и,  в  частности,  о  косом  скачке  уплотнения  приведены  в  работах  [16],  [30].

Несмотря  на  повсеместное  распространение  вычислительных  методов  газовой  динамики  в  ряде  приложений  актуальной  является  задача  непосредственного  расчета  скачков  уплотнения,  особенно,  если  нужно  найти  оптимальное  решение. 

В  многочисленной  имеющейся  литературе  на  эту  тему  методики  расчета  скачков,  как  правило,  приведены  в  форме,  затрудняющей  их  применение  в  задачах  оптимизации  и  управления  сверхзвуковыми  течениями. 

Положение  осложняется  тем,  что  уравнения,  связанные  с  расчетом  скачков,  часто  имеют  несколько  решений,  вычислительные  особенности  или,  вообще,  явно  не  разрешены  относительно  искомой  переменной.  Для  отбора  решений,  которые  соответствуют  физически  реализуемым  ударно-волновым  конфигурациям,  получения  значений  в  окрестности  особых  точек  необходимо  привлекать  дополнительные  соображения. 

С  другой  стороны,  существует  минимальный  набор  важнейших  характеристик  скачков,  для  которых  возможна  постановка  задачи  расчета  в  удобной  форме.  Знание  особых  и  предельных  параметров  скачков  позволяет  легко  разделять  решения  на  классы. 

В  настоящей  работе  изложен  именно  такой  подход,  позволяющий  просто  и  без  затруднений  решить  90  %  практически  значимых  задач,  связанных  с  расчетом  одиночных  косых  скачков  уплотнения.

Подробный  анализ  газодинамических  волн  (изоэнтропических  волн  разрежения  и  сжатия)  и  косых  скачков  уплотнения,  возникающих  в  плоских  стационарных  течениях  невязкого  нетеплопроводного  совершенного  газа,  был  опубликован  в  1908  году  Т.  Майером  [23].  В  этой  же  работе  определены  параметры  косого  скачка  уплотнения,  образующегося  при  обтекании  плоского  острого  угла.  Буземан  в  ряде  работ  в  1929—1937  годах  [5],  [17],  [18]  заложил  основу  графических  методов  решения  задач  об  интерференции  газодинамических  разрывов  с  помощью  ударных  поляр,  связывающих  интенсивность  косых  скачков  уплотнения  с  углом  разворота  потока  на  скачке.  Ударные  поляры  именно  с  того  времени  называются  в  его  честь  полярами  Буземана.  За  характерный  вид  их  еще  называют  сердцевидными  кривыми.  Еще  одно  название  —  изомахи,  т.  к.  каждая  ударная  поляра  строится  при  конкретном  числе  Маха  набегающего  потока.  Методы  решения  задач  интерференции  разрывов  с  помощью  ударных  поляр  были  развиты  Курантом  в  работе  [20].

Задачи  проектирования  сверхзвуковых  летательных  аппаратов  вызвали  в  40-е  годы  исследования  скачков  уплотнения,  взаимодействий  между  собой  отдельных  волн  и  разрывов.  В  первых  экспериментах  с  помощью  ударной  трубы  были  изучены  одномерные  взаимодействия.  Теория  течения  газа  в  ударной  трубе  в  одномерной  постановке  предложена  Шардиным  в  1932  году  [26].  В  Университете  Торонто  в  50-е  годы  был  проведен  ряд  экспериментальных  и  теоретических  работ  по  исследованию  взаимодействия  одномерных  бегущих  волн  и  разрывов: 

рефракция  бегущей  ударной  волны  на  контактном  разрыве  —  Битондо  и  другие  [15],  Битондо  [14],  Форд  и  Гласс  [21];

взаимодействие  догоняющих  ударных  волн  —  Гоулд  [22]; 

ударной  волны  с  волной  разрежения  —  Гоулд  [22],  Ничолл  [25]  и  рефракция  волны  разрежения  —  Биллингтон  и  Гласс  [13],  Биллингтон  [12]. 

Теоретические  результаты  в  эти  годы  были  скромнее.  В  работе  Тауба  [28]  исследовано  распространение  ударной  волны  по  двум  первоначально  покоящимся  газам,  разделенным  поверхностью  раздела  (контактным  разрывом).  В  1960  году  Молдер  [24]  разработал  аналитическую  теорию  регулярного  взаимодействия  встречных  ударных  волн.  Двух  и  трехмерные  задачи  долгое  время  решались  исключительно  численными  методами.

Большой  вклад  в  разработку  теории  стационарных  газодинамических  разрывов  внес  В.Н.  Усков.  В  современном  виде  её  основные  положения  были  сформулированы  в  1980  г.  в  учебном  пособии  [8].  В  сборнике  [7]  были  приведены  условия  динамической  совместности  для  основных  задач  об  интерференции  разрывов.  Результаты  анализа  соотношений  на  скачке  и  свойств  различных  ударно-волновых  структур  приведены  в  монографии  [9]. 

В  дальнейшем  они  были  развиты  на  случай  одномерных  бегущих  волн,  а  также  косых  ударных  волн  [10].  В  этих  работах  приведены  удобные  формулы  для  расчета  параметров  косых  скачков  уплотнения  и  косых  ударных  волн.  Проведенное  В.Н.  Усковым  исследование  сердцевидных  кривых  позволило  установить  их  важные  свойства:  наличие  огибающей,  предельных  углов  отклонения  потока  на  разрыве,  точек,  соответствующих  разрывам,  числа  Маха  за  которыми  равны  единице.  Можно  отметить,  что  наличие  огибающей  важно  в  задачах  сверхзвуковой  аэродинамики  летательных  аппаратов  [11],  т.  к.  соответствует  экстремумам  давления  на  сторонах  тела,  летящего  с  заданным  углом  атаки,  но  с  переменной  скоростью. 

Общность  математического  аппарата  одномерных  нестационарных  и  двумерных  стационарных  задач  о  взаимодействии  волн  и  разрывов,  продемонстрированная  в  работах  В.Н.  Ускова  и  Л.П.  Архиповой  [32],  [2],  позволила  М.Г.  Чернышову  решить  ряд  практически  важных  задач  [1],  [29],  [31],  [4]  о  взаимодействии  косого  скачка  с  волной  Прандтля-Майера.  Следующим  шагом  стало  исследование  взаимодействия  ударной  волны  и  прямого  скачка  уплотнения  [27],  а  также  косых  ударных  волн  [3]  и  нестационарных  тройных  конфигураций  [6].

1.  Косой  скачок  уплотнения  —  математическая  модель 

Моделью  ударных  волн  является  поверхность  математического  разрыва  первого  рода,  при  переходе  через  которую  газодинамические  переменные  терпят  разрыв  [f]=f2-f1.  Ударная  волна  в  общем  случае  может  перемещаться  в  пространстве.  Неподвижная  ударная  волна  называется  стоячей  волной  или  скачком  уплотнения.  Скачок,  расположенный  под  углом  к  набегающему  потоку,  называется  косым.  Соотношения  переменных  f2  и  f1  по  разные  стороны  газодинамических  разрывов  получили  название  условий  динамической  совместимости  (УДС)  на  скачке. 

Угол  наклона  скачка  σ,  его  интенсивность  J,  под  которой  обычно  понимают  отношение  давления  за  скачком  P2  к  давлению  перед  скачком  P1,  и  угол  отклонения  потока  на  скачке  β  (рисунок  1a)  при  заданных  параметрах  течения  перед  скачком  (M1,  P1,  P01,  ρ)  уплотнения  взаимно  однозначно  связаны  между  собой.  Задание  любого  из  этих  трех  параметров  позволяет  вычислить  два  других.  Если  известен,  например,  угол  разворота  потока  β,  как  на  рисунке  1b,  когда  он  равен  углу  клина,  на  который  натекает  сверхзвуковой  поток,  то  можно  найти  интенсивность  и  угол  наклона  образующегося  косого  скачка.  Если  известна  интенсивность  J,  например,  как  в  перерасширенной  струе,  когда  она  равняется  отношению  давлений  в  окружающей  среде  к  давлению  на  срезе  сверхзвукового  сопла  (точка  А,  рисунок  1c),  то  можно  найти  угол  наклона  скачка  и  угол  разворота  потока  (границы  струи)  на  скачке.  В  задачах,  когда  скачок  является  результатом  интерференции  других  разрывов,  чаще  всего  известен  его  угол  наклона,  по  которому  можно  вычислить  интенсивность  и  угол  разворота  потока.

 

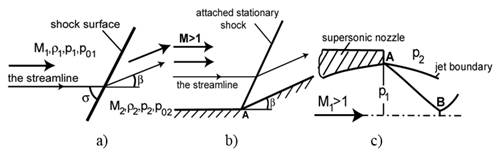
Рисунок  1.  Определение  косого  скачка  уплотнения  индексы:  1  —  параметры  до  скачка,  2  —  параметры  за  скачком,  M  —  число  Маха,  P  —  давление,  P₀  —  полное  давление,  β  —  угол  разворота  потока,  σ  —  угол  наклона  скачка  уплотнения.

 

Параметры  скачка  уплотнения  зависят  от  теплофизических  свойств  газа,  которые  выражаются  показателем  адиабаты  γ  =  cp/cv  (cp  —  удельная  теплоемкость  газа  в  термодинамических  процессах,  происходящих  при  постоянном  давлении,  cv-  удельная  теплоемкость  газа  в  термодинамических  процессах,  происходящих  при  постоянном  объеме),  а  также  его  молекулярным  весом.  Показатель  адиабаты  в  идеальном  газе  зависит  от  числа  степеней  свободы  атома  γ=(j+2)/j.  Если  газ  одноатомный,  то  степеней  свободы  у  него  3,  и  показатель  адиабаты  равен  5/3  или  1,666...  Если  газ  двухатомный,  то  степеней  свободы  у  него  5,  и  показатель  адиабаты  равен  7/5  или  1,4.  Если  газ  трехатомный,  то  степеней  свободы  у  него  6,  и  показатель  адиабаты  равен  8/6  или  1,333…  Кроме  того,  обычно  выделяют:  γ=1.1  для  смеси  углеводородного  топлива  с  воздухом,  γ=1.2  -  для  смеси  углеводородного  топлива  с  кислородом,  γ=1.25  -  для  продуктов  сгорания.  В  реальном  газе  γ  зависит  от  давления  и  температуры,  но  этим  можно  пренебречь  при  t<600Κ.

УДС  на  стационарных  разрывах  представляют  собой  равенство  нулю  скачка  следующих  газодинамических  параметров  [f]=f2-f1:

потока  вещества

 

  ,  (1)

 

импульса  движения  в  проекции  на  нормаль  к  поверхности  скачка

 

  (2)

 

импульса  движения  в  проекции  на  касательную  к  поверхности  скачка

 

,  (3)

 

Энергии

 

,  (4)

 

где    и    проекции  вектора  скорости  на  плоскость  разрыва,  i  —  энтальпия.  Давление  P,  температура  T  и  плотность  связаны  уравнением  состояния  Менделеева-Клайперона

 

,  (5)

 

которое  для  идеального  газа  (молекулярный  вес  и  показатель  адиабаты  постоянны,  энтальпия  i  пропорциональна  температуре  T)  может  быть  переписано  в  виде:

 

.  (6) 

 

Степень  сжатия  потока  в  ударно-волновом  процессе  принято  характеризовать  отношением  плотностей  E=ρ1/ρ2,  которые  в  отсутствие  внешнего  подвода  тепла  называются  адиабатой.  Если  Ε>1,  то  имеет  место  расширение  потока,  если  <1,  то  сжатие.  В  изоэнтропическом  процессе  Ε  определяется  адиабатой  Лапласса-Пуассона  (изоэнтропа)

 

.  (7)

 

На  скачке  уплотнения  с  помощью  (6)  и  системы  (2,3)  уравнение  энергии  (4)  можно  записать  в  виде  уравнения  ударной  адиабаты  Рэнкина-Гюгонио

 

.  (8)

 

Скачков  разрежения  не  бывает,  т.  е.  на  скачке  всегда  Ε<1.  Часто  в  соотношениях  вместо  γ  используется  величина 

 

,  (9)

 

которая  представляет  собой  предел  E  при  J→∞.  Видно,  что  на  скачке  он  конечен,  т.  е.  плотность  не  может  возрастать  бесконечно.  Адиабата  Рэнкина-Гюгонио  может  быть  записана  в  виде  зависимости  от  интенсивности  скачка

 

.  (10)

 

Введем  число  Маха  M=v/a,  где  a  –  местная  скорость  звука:

 

.  (11)

 

Тогда  после  несложных  преобразований  из  уравнений  (1—4),  с  учетом  (10,11)  можно  получить  выражение  для  интенсивности  косого  скачка  уплотнения

 

,  (12)

 

а  также  связь  между  углами  поворота  потока  β  и  наклона  скачка  σ 

 

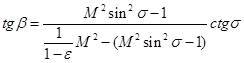  .  (13)

 

Уравнения  (12—13)  определяют  при  заданном  М  ударную  поляру  lnJ-β,  (рисунок  2)  в  параметрической  форме  с  параметром  σ,  который  может  меняться  в  пределах  от  угла  Маха  α=arcsin  (1/M)  до  90°.  Видно,  что  для  каждого  числа  Маха  имеется  максимальная  интенсивность

 

,  (14) 

 

с  использованием  которой  угол  β  можно  выразить  следующим  образом

 

.  (15)

 

Если  скачок  задан  интенсивностью  J,  то  для  вычисления  угла  β  удобнее  использовать  (15),  если  углом  разворота  σ,  то  —  (13). 

 

Рисунок  2.  Ударная  поляра  при  γ=1.4,  число  Маха  изменяется  от  2  до  5  с  шагом  0.2

 

Если  скачок  задан  углом  разворота  потока  β,  то  удобнее  решать  уравнения  (13),  (15)  численно,  хотя  существует  кубическое  уравнение  относительно  J,  явно  связывающее  J-β.  Для  каждого  β  получается  два  решения  для  скачков:  со  сверхзвуковым  течением  за  ним  и  с  дозвуковым.  Отношение  переменных  на  скачке  можно  записать  только  с  помощью  интенсивности  J  и  обобщенной  адиабаты  E

 

,  (16)

 

отношение  температур

 

,  (17)

 

отношение  скоростей  звука

 

,  (18)

 

коэффициент  восстановления  полного  давления

 

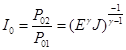,  (19)

 

отношение  плотностей

 

.  (20)

 

Записанные  в  таком  виде  соотношения  справедливы  для  любых  типов  волн:  простых,  ударных  и  детонационных.  Если  вместо  E  в  соотношения  (16)—(20)  подставить  уравнения  адиабаты  Лапласа-Пуассона  (7),  то  получим  соотношения  для  простых  и  центрированных  изоэнтропических  волн.  Если  подставить  адиабату  Рэнкина-Гюгонио  (10),  то  получим  уравнения  для  ударных  волн.  Все  переменные  за  скачком  в  уравнениях  (16—20)  монотонно  изменяются  в  зависимости  от  интенсивности  скачка  J.

2.  Результаты  анализа  ударных  поляр

На  рисунках  2—5  представлены  ударные  поляры  для  разных  γ,  при  М=2-5.  Меньшая  поляра  соответствует  меньшему  числу  Маха.

 

Рисунок  3.  Ударная  поляра  при  γ=1.1,  число  Маха  изменяется  от  2  до  5  с  шагом  0.2

 

Рисунок  4.  Ударная  поляра  при  γ=1.25,  число  Маха  изменяется  от  2  до  5  с  шагом  0.2

 

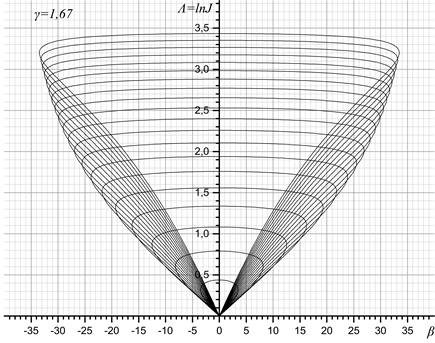
Рисунок  5.  Ударная  поляра  при  γ=1.67,  число  Маха  изменяется  от  2  до  5  с  шагом  0.2

 

Часто  возникает  практически  значимая  задача  затормозить  поток  до  скорости  меньше  скорости  звука,  поэтому  полезно  уметь  по  заданному  числу  М  набегающего  потока  вычислять  интенсивность  скачка,  за  которым  М=1

 

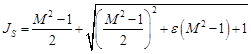.  (21)

 

Актуальной  является  и  обратная  задача  —  вычисление  по  заданной  интенсивности  скачка  числа  Маха  набегающего  потока,  при  котором  течение  за  скачком  становится  звуковым

 

.  (22)

 

Если  течение  за  присоединенным  к  клину  скачком  дозвуковое,  то  размеры  клина  влияют  на  течение  у  его  вершины. 

Для  каждого  М  и  γ  существует  предельный  угол  β,  на  который  косой  скачок  способен  отклонить  поток.  Следовательно,  картина  течения,  изображенная  на  рисунке  1b  возможна  только  при  небольших  углах  клина  β.  Если  же  он  превышает  некоторое  предельное  для  данного  М  значение,  которое  принято  обозначать  βl,  то  образуется  отошедший  криволинейный  скачок  уплотнения  (рис.  6). 

 

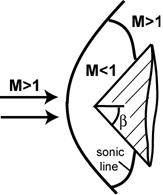
Рисунок  6.  Картина  течения  при  угле  клина,  большем  β

 

Интенсивность  скачка,  способного  развернуть  поток  на  максимально  возможный  угол  βl,  выражается  соотношением

 

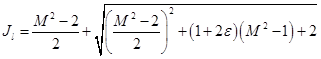.  (23)

 

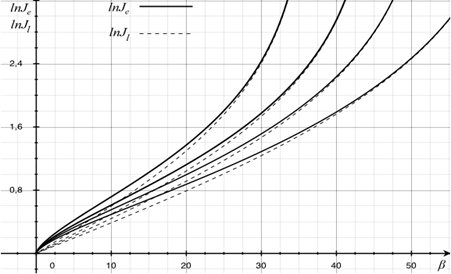
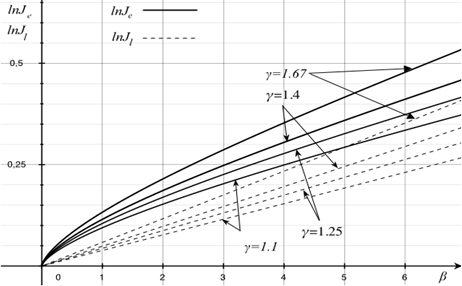
Подставляя  (23)  в  (15),  получим  значение  предельного  угла  разворота  потока.  Соответственно,  можно  построить  предельную  поляру  J_l-β_l  (рисунок  7).

 

a)

b) 

Рисунок  7.  Зависимости  для  предельного  угла  отклонения  потока  J_l-β_l  и  огибающей  семейства  поляр  J_e-β_e

 

Точка  на  сердцевидной  кривой,  соответствующая  J_l,  делит  поляру  на  две  части.  Часть  кривой,  лежащая  ниже  этой  точки,  соответствует  присоединенным  скачкам,  часть,  лежащая  выше,  отошедшим. 

Предельный  угол  отклонения  βl  растет  с  увеличением  М  и  при  равняется  48.58º  для  γ=1.4  (рисунок  8). 

 

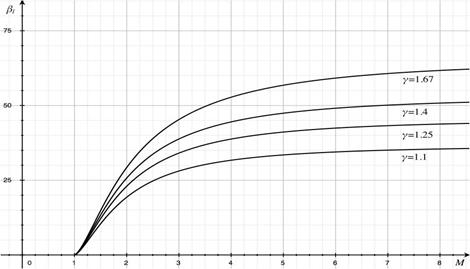
Рисунок  8  Зависимости  для  предельного  угла  отклонения  потока  J_l  от  числа  Маха

 

Угол  же  наклона  скачка  σl,  при  котором  достигается  предельный  угол  отклонения  потока  βl  ,  зависит  от  числа  Маха  немонотонно.

Через  произвольную  точку  координатной  плоскости  {J;β}  могу  проходить  две  ударные  поляры,  соответствующие  разным  числам  Маха,  что  определяет  наличие  огибающих  ударных  поляр  ограничивающих  на  плоскости  {J;β}  область,  занимаемую  ударными  полярами  при  1<M<∞.  В  параметрическом  виде  уравнение  огибающих  имеет  вид 

 

,  (24)

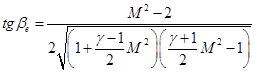.  (25)

 

Так  как  на  скачках  уплотнения  J>1,  то  из  (24)  следует,  что  ударные  поляры  при  M<2^1/2  не  имеют  огибающей.  Угол  поворота  потока  на  скачке  с  интенсивностью  Je  максимален  по  сравнению  со  всеми  скачками  той  же  интенсивности,  возникающими  в  потоке  с  другими  числами  Маха.  Огибающая  показана  на  рисунке  7.

На  любой  поляре  можно  выделить  особые  точки  e,  s,  l,  причем  всегда  выполняется  неравенство  Je<Js<Jl.

Используя  приведенные  выше  графики,  можно  решать  графически  задачи  об  интерференции  газодинамических  разрывов.  Продемонстрируем  это  на  примере  пересечения  двух  скачков  уплотнения  одного  направления  (рисунок  9).

 

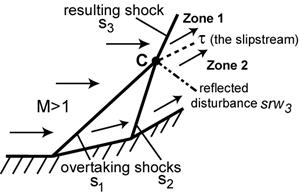
Рисунок  9.  Пересечение  двух  скачков  ( s₁  и  s₂)  одного  направления  с  образованием  третьего  результирующего  скачка  s₃

 

Этому  случаю  на  плоскости  ударных  поляр  соответствует  пересечение  двух  ударных  поляр  (рисунок  10).  На  основной  поляре,  соответствующей  числу  Маха  М,  отмечается  точка  с  координатами  Λ1-β1.  Из  этой  точки  выпускается  вторая  ударная  поляра,  построенная  по  числу  Маха  за  скачком  s1.  Поляры  пересекаются  в  точке  1—3,  координаты  которой  определяют  интенсивности  Λ2,  Λ3  и  углы  разворота  потока  β2,  β3  для  скачков  s2,  s3.

 

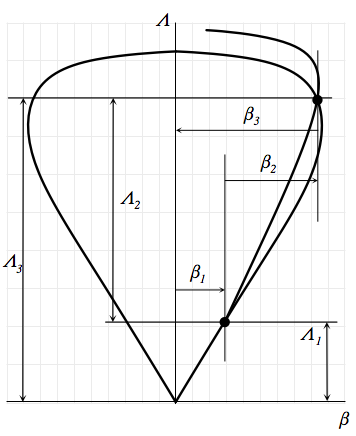
Рисунок  10.  Решение  на  плоскости  поляр  задачи  об  интерференции  двух  скачков  уплотнения  одного  направления

 

ЗАКЛЮЧЕНИЕ

Приведены  универсальные  формулы  для  расчета  параметров  за  скачком,  записанные  с  помощью  обобщенной  адиабаты,  применимые  также  для  простых  волн  и  детонационных  волн  (при  использовании  соответствующих  выражений  для  адиабаты).  Эти  формулы  позволяют  вычислить  параметры  скачка,  если  известно  значение  хотя  бы  одной  газодинамической  переменной  за  ним. 

Если  известны  параметры  потока  перед  скачком  и  интенсивность  скачка,  то  данные  уравнения  позволяют  вычислить  все  параметры  за  скачком.  Результаты  расчетов  зависимости  важнейших  характеристик  скачков  от  числа  Маха  и  показателя  адиабаты  потока  приведены  в  удобной  для  непосредственного  использования  форме.  Рассматривая  точки  пересечения  поляр,  построенных  при  разных  числах  Маха,  можно  находить  параметры  скачков  в  соответствующих  ударно-волновых  структурах

 

Список  литературы:

1. Архипова  Л.П.,  Усков  В.  Н.  2012.  “Отражение  Центрированной  Волны  Разрежения  Римана  Со  Сверхзвуковым  Задним  Фронтом  От  Твердой  И  Гладкой  Стенки.”  Вестник  СПбГУ.  Серия  1  (Вып.  4):  —  С.  62—67.
2. Архипова  Л.П.,  Усков  В.  Н.  2013.  “Универсальное  Решение  Задачи  Об  Отражении  Одномерных  Бегущих  Волн  От  Твердой  Поверхности  И  Их  Анализ  Для  Волн  Уплотнения.”  Вестник  СПбГУ.  Серия  1  (Вып.  2):  —  С.  77—81.
3. Усков  В.Н.,  Карасев  К.  А.  2003.  “Критериальные  Интенсивности  При  Интерференции  Прямого  Скачка  Уплотнения  И  Встречной  Ударной  Волны.”  Сб.  “Наука  и  технологии”.  —  С.  4—11.
4. Усков  В.Н.,  Мешков  В.Р.,  Омельченко  А.  В.  2002.  “Взаимодействие  Скачка  Уплотнения  Со  Встречной  Волной  Разрежения.”  Вестник  СпбГУ.  Сер.  1  (Вып.  2).
5. Усков  В.Н.,  Мостовых  П.  С.  2008.  “Тройные  Конфигурации  Бегущих  Ударных  Волн  В  Потоках  Невязкого  Газа.”  ПМТФ.  Т.  49(№  3):  —  С.  3—10.
6. Усков  В.Н.,  Омельченко  А.  В.  2002.  “Интерференция  Нестационарных  Косых  Ударных  Волн.”  Письма  в  ЖТФ.  Т.  28  (№  12):  —  С.  5—12.
7. Усков  В.Н.  Интерференция  стационарных  газодинамических  разрывов/  “Сверхзвуковые  Газовые  Струи”.  -  Новосибирск:  ИТПМ,  1983.  —  С.  22—46.
8. Усков  В.Н.  Ударные  волны  и  их  взаимодействие.  -  Л.:  ЛМИ,  1980.  —  88  с.
9. Усков  В.Н.,  Адрианов  А.Л.,  Старых  А.Л.  Интерференция  стационарных  газодинамических  разрывов.  Новосибириск:  ВО  “Наука”.  Сибирская  Издательская  Фирма.  1995.  —  С.  180.
10. Усков  В.Н.,  Тао  Ган,  Омельченко  А.В.  О  Поведении  Газодинамических  Переменных  За  Косой  Ударной  Волной/  Сб.  статей//  Под.  ред.  В.Н.  Ускова.  2002.  —  С.  179—191.
11. Усков  В.Н.,  Чернышов  М.В.  Экстремальные  ударно-волновые  системы  в  задачах  внешней  аэродинамики  //  Теплофизика  и  аэромеханика.  —  Т.  21.  —  2014.  —  №  1.  —  C.  15—31. 
12. Billington  I.I.  (1955)  An  Experimental  Study  of  One–Dimensional  Refraction  of  a  Rarefaction  Wave  at  a  Contact  Surface.  University  of  Toronto  Institute  for  Aerospace  Studies  (UTIAS)  Report  №  32. 
13. Billington  I.I.,  Glass  I.I.  (1955)  On  the  One–Dimensional  Refraction  of  a  Rarefaction  Wave  at  a  Contact  Surface.  University  of  Toronto  Institute  of  Aerophysics  (UTIA)  Report  №  31. 
14. Bitondo  D.  (1950)  Experiments  on  the  Amplification  of  a  Plane  Shock  Wave.  University  of  Toronto  Institute  of  Aerophysics  (UTIA)  Report  №  7. 
15. Bitondo  D.,  Glass  I.I.,  Patterson  G.N.  (1950)  One  Dimensional  Theory  of  Absorption  and  Amplification  of  a  Plane  Shock  Wave  by  a  Gaseous  Layer.  University  of  Toronto  Institute  of  Aerophysics  (UTIA)  Report  №  5.
16. Bulat  P.V.,  Uskov  V.N.,  2014.  Shock  and  detonation  wave  in  terms  of  view  of  the  theory  of  interaction  gasdynamic  discontinuities.  Life  Science  Journal,  11(8s):  307-310.
17. Busemann  A.  Gasdynamik,  Handbuch  der  ex-  perimentellen  Physik  [Text]  /  A.  Busemann.  –  Leipzig:  Akademischer  Verlag,  —  1931.  —  Vol.  IV,  —  Part.  1.  —  394  s.
18. Busemann  A.  Hodographenmethode  der  Gas-  dynamik  [Text]  /  A.  Busemann  //  ZAMM.  —  1937.  —  Vol.  17,  —  Issue  2.  —  P.  73—79.
19. Busemann  A.  Verdichtungsstӧße  in  ebenen  Gasstrӧmungen.  Vorträge  aus  dem  Gebiet  der  Aerody-  namik,  Aachen  1929  [Text]  /  A.  Busemann;  heraus-  gegeben  von  A.  Gilles,  L.  Hopf  und  Th.  von  Kàrmàn.  –  Berlin:  Julius  Springer,  1930.  —  S.  162—169.
20. Courant  R.,  Friedrichs  K.O.  (1948)  Supersonic  flow  and  shock  waves.  New  York.
21. Ford  C.A.,  Glass  I.I.  (1956)  An  Experimental  Study  of  One–Dimensional  Shock  Wave  Refraction.  J.  Aero.  Sci.  —  Vol.  23,  —  №  2,  —  pp.  189—191. 
22. Gould  D.G.  (1952)  The  Head–On  Collision  of  Two  Shock  Waves  and  a  Shock  and  Rarefaction  Wave  in  One–Dimensional  Flow.  University  of  Toronto  Institute  of  Aerophysics  (UTIA)  Report  №  17.
23. Meyer  Th.  (1908)  Ueber  zweidimensionale  Bewegungsvorg ̈ange  in  einem  Gas,  dasmit  Ueberschallgeschwindigkeit  str ̈omt  //  Forschungsheft  des  Vereins  deut-  cher  Ingenieure,  Bd.  62,  —  S.  31—67. 
24. Molder  S.  (1960)  Head–on  interaction  of  oblique  shock  waves.  University  of  Toronto  Institute  for  Aerospace  Studies  (UTIAS)  Technical  Note  №  38.  September. 
25. Nicholl  C.I.H.(1951)  The  Head–On  Collision  of  Shock  and  Rare-factionWaves.  University  of  Toronto  Institute  of  Aerophysics  (UTIA)  Report  №  10.
26. Schardin  H.  (1932)  Physik.  Zeits.  33,  60. 
27. Silnikov  M.V.,  Chernyshov  M.V.,  Uskov  V.N.  Analytical  solutions  for  Prandtl-Meyer  wave  —  oblique  shock  overtaking  interaction  //  Acta  Astronautica.  —  2014.  —  Vol.  99.  —  Pp.  175—183.
28. Taub  A.H.  (1947)  Refraction  of  Plane  Shock  Waves.  Physical  Review.  Vol.  72.  №  1.  July  1. 
29. Uskov  V.,  Chernyshov  M.  2013.  “The  Interaction  of  Prandtl-Meyer  Wave  with  the  Oblique  Shock  of  the  Same  Direction.”  Journal  of  Energy  and  Power  Engineering.  Vol.  4(№  6):  —  P.  21.
30. Uskov  V.N.,  Bulat  P.V.,  Arkhipova  L.P.  Gas-dynamic  Discontinuity  Conception.  Research  Journal  of  Applied  Sciences,  Engineering  and  Technology,  —  2014,  —  Vol.  8,  (22).  —  p.  2255—2259.
31. Uskov  V.N.,  Chernyshov  M.  V.  2010.  “Analytical  Solutions  for  Overtaking  Prandtl-Meyer  Wave  —  Oblique  Shock.”  19th  International  Shock  Interaction  Symposium.  —  P.  4.
32. Uskov  V.N.,  Chernyshov,  M.V.  Extreme  shockwave  systems  in  problems  of  external  supersonic  aerodynamics  //  Thermophysics  and  Aeromechanics.  —  Vol.  21.  —  2014.  —  №  1.  —  p.  15—30.