ТЕПЛОПЕРЕДАЧА  ПРИ  ДВИЖЕНИИ  ЖИДКОСТИ  В  ТРУБЕ

Шевченко  Сергей  Николаевич

канд.  техн.  наук,  доцент, 
Балтийский  военно-морской  институт, 
РФ,  г.  Калининград

E -mail:  shevchenko_s@baltnet.ru

Шинкарева  Нина  Владимировна

канд.  физ.-мат.  наук,  доцент, 
Балтийский  военно-морской  институт, 
РФ,  г.  Калининград

Гузнаева  Ольга  Геннадьевна

канд.  пед.  наук,  доцент, 
Балтийский  военно-морской  институт, 
РФ,  г.  Калининград

HEAT  TRANSFER  AT  FLOW  OF  FLUID  IN  THE  TUBE

Sergey  Shevchenko

PhD,  Associate  Professor,  Baltic  Naval  Institute , 
Russia,  Kaliningrad

Nina  Shinkareva

PhD,  Associate  Professor,  Baltic  Naval  Institute, 
Russia,   Kaliningrad

Olga  Guznaeva

PhD,  Associate  Professor,  Baltic  Naval  Institute, 
Russia,   Kaliningrad

АННОТАЦИЯ

  Рассмотрена  задача  изменения  температуры  жидкости  при  движении  теплоносителя  с  учетом  переменного  коэффициента  теплопередачи.  Получено,  что  учет  зависимости  коэффициента  теплопередачи  от  теплофизических  характеристик  жидкости  приводит  к  повышению  расчетной  температуры  теплоносителя.

ABSTRACT

The  task  of  changing  the  temperature  of  the  liquid  heat  transfer  agent  in  the  motion  with  the  variable  heat  transfer  coefficient.  It  was  found  that  the  inclusion  of  the  heat  transfer  coefficient  depending  on  the  thermal  characteristics  of  the  fluid  increases  the  estimated  temperature  of  the  heat  transfer  agent.

Ключевые  слова:  коэффициент  теплопередачи;  тепловой  поток;  жидкость;  температура.

Keywords:  heat  transfer  coefficient;  heat  flow;  fluid;  temperature.

Пусть  в  начальном  сечении  А  (рис.  1)  температура  жидкости  t_A  и  температура  окружающей  среды  t₀.  Расход  жидкости  G_ж.  Выделим  элемент  трубы  длиной  dx  и  составим  баланс  тепла  на  этом  участке.

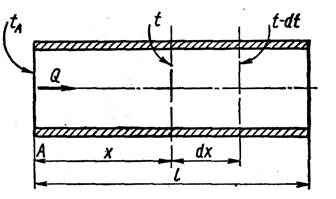
Рисунок  1.  Схема  движения  жидкости  при  изменении  температуры  теплоносителя

Потеря  тепла  Q₁  на  участке  dx  вследствие  охлаждения  равна.  Если  температура  внешней  среды  t₀,  то  количество  тепла,  отданного  на  участке  dx  во  внешнюю  среду,  равно  .  Потери  напора  на  участке  трубы  ,  где    —  пьезометрический  уклон.  Тогда    и  уравнение  баланса  тепла  имеет  вид  ,  где  g  —  удельный  объем.  Если  K=const,    или.  Или,  .  Обозначив    и    имеем  .  Разделим  переменные  и  проинтегрируем  ;  ;  .  Соответственно,  .  В  [1]  допущена  ошибка  при  интегрировании  данного  уравнения,  где  в  результате  получено  .  Так  как  при  х  =  0,  t  =  t_A.  Следовательно,  .  Отсюда,    Тогда  .  Окончательно  закон  распределения  температур  по  длине  трубы  имеет  вид  .  Если  пренебречь  теплотой  трения,  то,  .  Данное  уравнение  называют  формулой  Шухова.  В  ряде  случаев  формула  имеет  другой  вид  [2]  ,  где  ;  a  —  коэффициент  теплоотдачи.  Если  х  =  l,  получаем    или  без  учета  трения  .  Учтем,  что  K  является  функцией  температуры.  Значения  K  =  f(t)  определяется  зависимостями  a₁  =  f₁(t),  l  =  f₂(t),  a₂  =  f₃(t).  Пусть  l  имеет  линейную  зависимость  от  температуры,  то  .  При  вынужденном  течении 

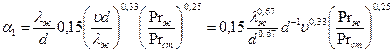
Если  принять  линейную  зависимость  l_ж  от  .  Тогда  .  Пусть  функция  n  =  f(t)  определяется  зависимостью  n  =  а₂  +  b₂t.  Тогда  для  свободного  теплообмена  с  внешней  стороны  .  После  преобразований  получаем

В  таком  случае  зависимость  коэффициента  теплопередачи  K  =  f(t)  будет  иметь  вид

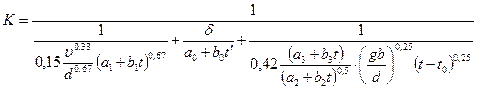
где    температурная  зависимость  коэффициента  теплопроводности  стенки  трубопровода.  Так  как  в  рассматриваемом  случае  коэффициенты  a  и  b,  являются  функциями  температуры  потока  теплоносителей,  то  уравнение  примет  следующий  вид  .  Тогда  .  Левый  интеграл  уравнения  равен

Так  как  t₀  является  постоянной  величиной,  то  .  Если  обозначить  величину  ,  тогда  первый  интеграл  приобретает  вид

Учитывая  зависимость  K(t)  от  температуры  теплоносителя  получаем

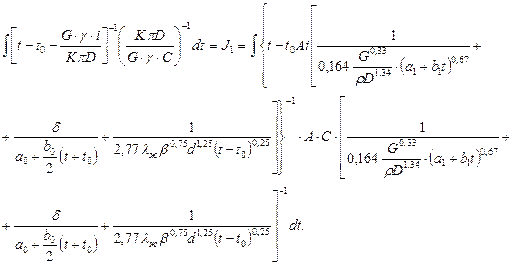
Если  обозначить  постоянные  величины,  входящие  в  подынтегральное  выражение  как  ;  ,  то  интеграл  приобретает  более  компактный  вид

Полученный  интеграл  не  интегрируется  в  квадратурах  и  получить  аналитическое  выражение  для  него  не  удается.  Однако  для  конкретного  трубопровода  при  постоянных  значениях  А,  С,  В₁,  В₂  можно  произвести  численное  интегрирование.  Так,  численный  расчет  показал,  что  при  движении  горячего  теплоносителя  (вода)  трубопровода  медного  теплообменника  с  толщиной  стенки  d  =  0,7  мм  и  внутренним  диаметром  D  =  15  мм,  температурой  t_A  =  96  °С,  t₀  =  20  °С,  l  =  4  м  увеличение  температуры  горячего  теплоносителя  по  сравнению  с  расчетами,  произведенными  по  формуле  Шухова  составляет  Dt  =  16  °С  или  12,4  %.

Таким  образом,  полученные  результаты  показывают,  что  при  учете  зависимости  теплофизических  параметров  теплоносителя  от  температуры,  конечная  расчетная  температура  потока  жидкости  в  теплообменнике  больше,  чем  при  K  =  const  в  среднем  на  10  ¸  12  %.  Приведенная  методика  расчета  позволяет  более  точно  определять  конечную  температуру  жидкости  и  тем  самым  увеличивает  точность  определения  тепловой  эффективности  теплообменника  в  целом.

Список  литературы:

1.Гавриленко  Б.А.,  Минин  В.А.,  Рождественский  С.Н.  Гидравлический  привод  М.:  Изд-во  Машиностроение.  1968.  —  502  с.

2.Чарный  И.А.  Основы  газовой  динамики  М.:  Гостехиздат.  1961.  —  200  с.