СПОСОБ  ЧИСЛЕННОЙ  ОЦЕНКИ  ЗАЩИЩЕННОСТИ  ОТ  ПРЕДНАМЕРЕННЫХ  ИСКАЖЕНИЙ  ИЗОБРАЖЕНИЙ  С  ИСПОЛЬЗОВАНИЕМ  РОБАСТНОЙ  ХЭШ  ФУНКЦИИ

Мартимов  Руслан  Юрьевич

старший  научный  сотрудник,  ОАО  СПбФ  «Концерн  Вега»,

РФ,  г.  Санкт-Петербург

E -mail:  Martimov.Ruslan@yandex.ru

NOVEL  APPROACH  FOR  NUMERICAL  ESTIMATES  ARE  PROTECTED  FROM  MODIFICATION  IMAGES  USING  ROBUST  HASH  FUNCTIONS

Ruslan  Martimov

senior  researcher  in  SPb  “Vega”, 
Russia,  St.  Peterburg

АННОТАЦИЯ

В  большинстве  сфер  деятельности  потребность  в  изображениях  и  видео  постоянно  растет.  При  этом  требуются  удобные  и  эффективные  методы  защиты  целостности  видовой  информации.  В  работе  представлен  новый  метод  оценки  защищенности  фрагментов  изображений  от  угроз  нарушения  целостности.  Метод  позволяет  получить  вероятность  необнаружения  преднамеренных  искажений.  В  качестве  непосредственно  инструмента  защиты  выступает  класс  робастных  хэш-функций,  предлагаемый  подход  оценки  легко  может  быть  обобщен  и  для  других  методов  защиты  целостности,  такие  как,  например,  цифровой  водяной  знак.

ABSTRACT

Nowadays,  the  need  in  image  and  video  is  increasingly  growing.  The  same  is  growing  need  for  easy-to-use,  and  effective  method  of  protection  against  modification.  The  paper  proposes  a  new  approach  to  evaluate  the  security  of  the  image  from  being  modifying.  That  lets  get  the  probability  of  not  detecting  modifications.  As  protection,  tools  used  class  robust  hash  functions,  although  the  proposed  approach  can  be  easily  extending  to  other  methods  of  protection,  for  example  digital  watermarks.

Ключевые  слова:  робастная  хэш  функция;  защита  целостности  изображений;  защита  информации

Keywords:  robust  hash  function;  protected  of  image  modification;

Для  обеспечения  удобной  и  эффективной  защиты  видовой  информации  все  чаще  используется  новый  класс  хэш-функций,  называемые  робастными  [1].  В  отличие  от  традиционных  криптографических,  данный  класс  хэш-функций  позволяет  обеспечить  робастность  к  допустимым  искажениям,  таким  как,  например,  сжатие  JPEG  или  пространственное  сжатие  I  кадров  в  H.264  видео-кодеке,  и  при  этом  позволяют  выявлять  преднамеренные  искажения. 

Существующие  большое  количество  подходов  защиты  от  преднамеренных  искажений  [7;8;  9].  При  этом  метод  принятия  решения  об  выявленной  модификации,  недостаточно  проработан,  а  тем-более  подходы  предварительно  оцени  защищенности. 

Предложим  способ,  позволяющий  связать  воедино  вносимые  преднамеренные  искажения  на  изображении  и  вероятность  их  детектирования.  Под  детектированием  понимается  изменение,  например,  расстояния  Хэмминга  [8]  на  величину  большую  заданного  порога.  Сам  же  этот  порог  выбирается  в  зависимости  от  робастных  свойств  хэш-функции. 

В  первую  очередь,  для  оценки  вносимых  искажений  необходимо  выбрать  метрику.  Рассмотрим  простейший  случай,  когда  такой  метрикой  выступает  нормированная  метрика  Минковского  [6]  4-степени  по  области  фиксированного  размера  W  на  H  пикселей  в  градациях  серого:

  (1)

где:  L  —  метрика  искажения, 

W  —  ширина  области  в  пикселях, 

H  —  высота  области  в  пикселях, 

  —  значение  яркости  пикселя  до  искажения, 

  —  после  искажения.  Четвертая  степень  берется  потому,  что  значение  метрики  получается  более  ровным,  чем  в  случае  со  2-ой.    —  максимальное  значение  искажения.  Соответственно  . 

В  качестве  метрики  показывающей  детектирование  будем  использовать  расстояние  Хэмминга.  Задача  состоит  в  том,  чтобы  построить  вероятностную  модель    ,  такую  что:

  (2)

Воспользовавшись  формулой  Байеса  [2],  можно  написать:

  (3)

где    —  условная  вероятность  необнаружения  при  заданном  L  и  порогового  расстояние  Хэмминга  с.  Таким  образом,  задача  сводится  к  восстановлению  плотности  функции  вероятности  ,  определению  вероятностей  P(с)  —  может  быть  получена  как  частота  возникновения  расстояния  с  при  моделировании  действий  нарушителя,  и  P(L)  —  вероятность  L,  зависящая  от  модели  нарушителя,  h  —  может  принимать  конечное  число  значений.  Если  длина  хэш-кода  составляет  256  бит,  то,  соответственно,  ,  0  —  значит  что  искажений  не  было  за  детектировано. 

Выполним  восстановление  плотности  отдельно  для  каждого  возможного  значения  с,  и  в  качестве  метода  для  удобства  выберем  параметрический  метод  [2].  А  в  качестве  описывающей  функции  –  обобщенное  распределение  экстремальных  значений  [1],  заданное  формулой 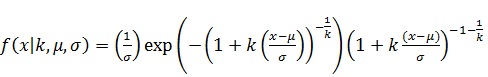 (4)

  (4)

В  ходе  исследований  формы  распределений  и  проверки  по  критерию  Хи-квадрат  [1],  было  установлено,  что  данная  функция  лучше  описывает  распределения.  В  качестве  альтернативных  распределений  рассматривались:  нормальное,  бета,  гамма  и  распределение  Вейбулла  [1]. 

В  соответствии  с  рассматриваемой  моделью,  искажения  L  —  случайная  величина  из  некоторого  распределения  с  плотностью  ,  где    —  вектор  параметров.  Плотность    описывает  возможное  множество  действий  нарушителя,  вносящих  преднамеренные  искажения.  Данное  распределение  и  его  параметры  подбираются  исходя  из  действий  нарушителя,  тех  целей,  которые  он  перед  собой  ставит.  Такими  действиями,  например,  может  быть  клонирование  одной  области  защищаемого  изображения,  копирование  из  одного  изображения  и  вставка  в  заверенное,  ухудшение  свойств  и  т.  д.

Тогда,  в  соответствии  с  длиной  хэш  кода  n,  общая  плотность  будет  представлена  набором  пересекающихся  плотностей  на  множестве  значений  L  для  всех  расстояний  Хэмминга.  Исходя  из  этого,  с  учетом  формулы  (4),  легко  вывести  формулу  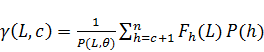(5)

  (5)

Где

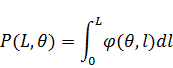
где:    —  кортеж  параметров  для  h  расстояния  Хэмминга  после  аппроксимации, 

L   —  исследуемое  искажение, 

с   —  исследуемое  пороговое  расстояние  Хэмминга. 

  —  вероятность  получения  заданного  расстояния  h,  получается  по  гистограмме. 

  —  априорная  вероятность  получения  L  исходя  из  модели  нарушителя. 

В  экспериментах  использовалась  стандартная  база  изображений  MIR  Flickr  [3].  Из  нее  были  взяты  2  непересекающиеся  случайные  подвыборки,  одна  для  обучения,  другая  для  тестирования.  Размеры  защищаемого  фрагмента  составляли  256  на  256  пикселей.  В  качестве  робастной  хэш-функции  была  взята  простейшая  функция  на  основе  дискретного  вейвлет  преобразования  с  квантованием  и  бинаризацией  низкочастотных  коэффициентов  [8].  В  опыте  случайным  образом  либо  клонировалась  область  одного  изображения,  либо  выполнялась  вставка  из  другого.  Для  обеспечения  достаточного  числа  экспериментов  области  тестирования  пересекались.  Число  экспериментов  составляло  порядка  двух  миллионов.  На  рисунке  1  представлена  гистограмма  обучающей  выборки,  а  на  рисунке  2  —  тестовой.

Тестовая  выборка  генерируется  по  той  же  модели  нарушителя,  что  и  обучающая,  но  как  было  указано  выше,  на  других  данных.  Данная  выборка  нужна,  для  того  чтобы  оценить  точность  предсказания  вероятности  детектирования  для  данного  L. 

Рисунок  1.  Обучающая  выборка  искажений

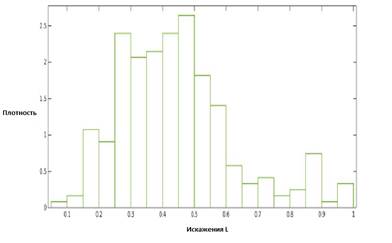
Рисунок  2.  Тестовая  выборка  искажений

Из  графика  на  рисунке  3  видно,  что  рабочей  областью  для  исследуемой  робастной  хэш-функции  ,  в  зоне  наиболее  точного  предсказания.  График  от  0,5  и  выше  идет  резко  вниз  по  причине,  в  основном,  недостатка  данных.  Это  следует  из  сопоставления  рисунков  1,  2,  3.  На  рисунке  4  представлен  итоговый  график  зависимостей  для  возможных  типовых  искажений.  Он  говорит,  с  какой  вероятностью  можно  получить  заданное  нормализованное  расстояние  Хэмминга.  Здесь  расстояние  Хэмминга  нормализуется,  для  того  чтобы  можно  было  исследовать  разные  длины  хэш-кода.

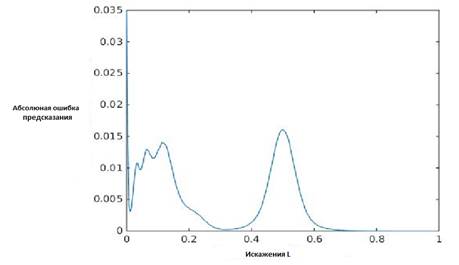
Рисунок  3.  Зависимость  ошибок  предсказания  от  L

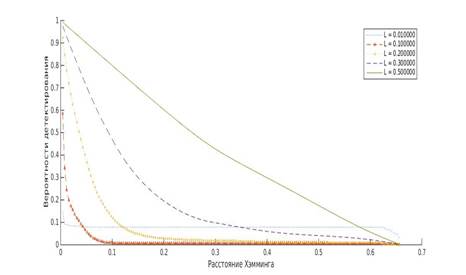
Рисунок  4.  Зависимость  вероятности  детектирования  от  требуемого  порогового  нормализованного  расстояния  Хэмминга  для  нескольких  искажений  L

Подводя  итог,  вероятность  необнаружения  искажений  рассчитывается  по  формуле 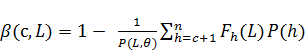 (6).

  (6)

Таким  образом,  был  представлен  метод  оценки  защищенности  фрагмента  изображения  от  атак  модификации.  В  качестве  инструмента  обеспечения  информационной  целостности  выступает  робастная  хэш-функция.  Один  из  ключевых  параметров,  позволяющих  оценить  защищенность,  —  это  точность  представления  вероятностной  модели  нарушителя,  связи  конкретных  его  целей  с  вносимыми  искажениями.  Данный  вопрос  заслуживает  отдельного  исследования  и  проработки.

Список  литературы:

1.Кобзарь  А.И.  Прикладная  математическая  статистика.  М.:  ФИЗМАТЛИТ,  2006.  —  812  с.

2.Машинное  обучение  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.machinelearning.ru/wiki/?title=Оценивание_плотности_распределения  (дата  обращения  20.06.2015). 

3.Тестовая  база  данных  изображений  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://press.liacs.nl/mirflickr/  (дата  обращения  20.06.2015) 

4.Флах  П.  Машинное  обучение  /  перевод  с  англ.  А.А.  Слинкина.  M.:  ДМК  Пресс,  2015.  —  400  с.:  ил. 

5.Электронная  энциклопедия.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ru.wikipedia.org/wiki/Расстояние_Хэмминга  (дата  обращения  20.06.2015).

6.Электронная  энциклопедия.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ru.wikipedia.org/wiki/Расстояние_Минковского  (дата  обращения  20.06.2015).

7.Brenden  Chong  Chen.  Robust  Image  hash  function  using  Higher  Order  Spector.  Laboratory  Science  and  Engendering  faculty,  2012.  —  185  с.

8.Venkatesan  R.,  S.-M.  Koon,  M.H.  Jakubowski  ,  and  P.  Moulin.  Robust  image  hashing,  2000  —  3  с.

9.Zhenjun  Tang,  Shuozhong  Wang,  Xinpeng  Zhang,  Weimin  Wei,  and  Shengjun  Su.  Robust  Image  Hashing  for  Tamper  Detection  Using  Non-Negative  Matrix  Factorization.  Journal  of  Ubiquitous  Convergence  and  Technology,  номер  7.  часть  1,  2008.  —  9  с.