МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ ВОЛН НАПРЯЖЕНИЙ ПРИ НАРУШЕНИИ СПЛОШНОСТИ УПРУГОЙ СРЕДЫ ТОНКОСТЕННЫХ КОНСТРУКЦИЙ

Патанин Андрей Владимирович

аспирант Сибирский государственный индустриальный университет,

г. Новокузнецк

Петрова Валентина Александровна

канд. техн. наук, доцент, Сибирский государственный индустриальный университет, г. Новокузнецк

Петров Валерий Иванович

канд. техн. наук, технический директор ООО «Виртуаль»,

 г. Новокузнецк

Меденков Александр Анатольевич

аспирант, Сибирский государственный индустриальный университет

г. Новокузнецк

Меденков Алексей Анатольевич

студент, Сибирский государственный индустриальный университет

г. Новокузнецк

E-mail: Medenkov_AA@inbox.ru

SIMULATION OF WAVE PROPAGATION OF PRESSURE AT DISTURBANCE MASSIVE OF AN ELASTIC MEDIUM OF THIN-WALL CONSTRUCTIONS

Andrew Patanin

The post-graduate student the Siberian state industrial university,

Of Novokuznetsk

Valentina Petrova

c.t.s., senior lecturer, Siberian state industrial university,

Of Novokuznetsk

Valerij Petrov

c.t.s., technical director ООО «Virtual»,

 of Novokuznetsk

Alexander Medenkov

The post-graduate student, Siberian state industrial university

Of Novokuznetsk

Alexei Medenkov

The student, Siberian state industrial university

Of Novokuznetsk

Аннотация

В работе рассматривается задача регистрации упругих волн, являющихся основополагающими при применении методов ультразвукового и акустического контроля. Особый интерес представляет исследование перераспределения энергии с учетом наличия свободных поверхностей материала и образовавшейся трещины. Таким образом, задача рассматривается в следующей постановке: требуется в первом приближении определить поля упругих напряжений и смещений, удовлетворяющие граничным условиям.

ABSTRACT

In activity the problem of registration of elastic waves being basic at application of methods of hypersonic and acoustic monitoring is considered. The soul interest represents a research of redistribution of energy with allowance for of availability of free surfaces of a stuff and derivated fracture. Thus, the problem is considered in following production: it is required as a first approximation to determine fields of elastic stresses and shifts satisfying to boundary conditions.

 Ключевые слова: ультразвуковой контроль; распространение волн напряжений; математическая модель; дефект.

Keywords: a ultrasonic control; wave propagation of pressure; mathematical model; defect.

 В качестве математической модели явления рассматривается плоская задача об излучении волн движущимся дефектом [1, 3] перпендикулярно свободной поверхности предварительно напряженного материала. Достаточно обстоятельно эта задача исследована в двух предельных случаях:

1.  При бесконечно малой длине трещины — плоская задача Лэмба. В этом случае подробно исследовано распределение энергии различных типов волн. В частности, показано, что энергетический вклад волн следующий: волны Рэлея — 67 % , поперечные — 26 %, продольные — 7 %. Однако в этом случае не учитывается влияние свободной поверхности, образуемой трещиной, что не позволяет автоматический перенос результатов исследований.

2.  Случай, когда свободная поверхность отнесена на бесконечность, то есть трещина полубесконечна. Основное внимание, однако, уделено процессам перераспределения энергии в вершине трещины, поэтому проведенный анализ для данной задачи не совсем приемлем.

Требуется в первом приближении определить поля упругих напряжений и смещений, удовлетворяющие граничным условиям:

где s_х , s_z , t — компоненты поля напряжения вдоль соответствующих осей, s₀ — приложенная нагрузка, z₀(t) — координата вершины трещины.

Напряжения и смещения внутри области удовлетворяют уравнениям движения (а) и закону Гука (б):

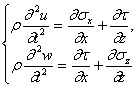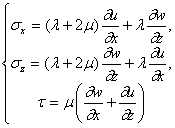   (а),  (б),

где l, m — постоянные Ламе; r — плотность материала; u , w — смещение вдоль координат x и z соответственно.

Вычитая равномерное поле напряжений s_х=s₀, s_z=t=0, перейдем к рассмотрению дополнительной задачи. Учитывая симметрию по координате в дополнительной задаче, имеем вместо вышеприведенных следующие граничные условия:

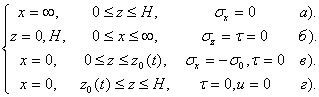
Данная задача является смешанной краевой задачей динамической теории упругости. В такой постановке анализ затруднителен, поэтому заменим условие (в) на приближенное:

при x=0,      0£z£z₀(t),    u=u₀ (z, t), t=0,

где u₀ (z, t) подбирается из соотношения:

.

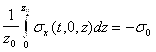Таким образом, на всей оси x=0 заданы смещения

u=u₀ (z, t), ^. Q [z₀ (t) - z],

где Q (y) — функция Хэвисайда.

Начальные условия предполагаются нулевыми:

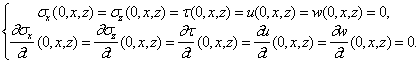
В такой постановке имеем:

u (t, x, z)=- u (t, -x, z), смещения u — функция нечетная;

w (t, x, z)=+w (t, -x, z), cмещения w — функция четная.

Это позволяет использовать для решения задачи преобразование

Фурье для u по синусам, а для w по косинусам: Определяются прообразы смещений:

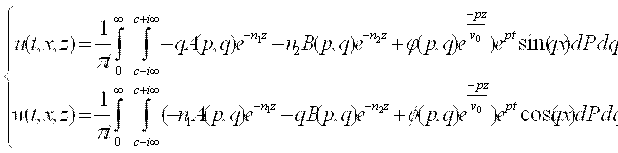
Из полученных интегральных представлений перемещений с помощью закона Гука [5, 4] можно получить все компоненты напряжений и, следовательно, вклад в перенос энергии соответствующих компонент волнового поля.

Количественной мерой локального смещения свободной поверхности является амплитуда, которая характеризуется плотностью кинетической энергии в данной точке. В продолжение вышеизложенного в данном получено решение в явном виде прообразов и представлено в удобной для эффективного численного исследования на ЭВМ форме. На основе этого решения проведен анализ вкладов в результирующее энергии продольных и поперечных волн и выбрана плотность кинетической энергии на свободной поверхности:

e (x, t)=.

Прямое вычисление интегралов представляет известные трудности, в связи с чем развито несколько методов вычислений прообразов. Для решения нашей задачи предлагается метод Каньяра-де Хупа в модификации Слепяна Л.И. [2].

I.  скорости отсутствуют: .

II.

III. .

В вышеприведенных выражениях С_R — скорость волн Рэлея;

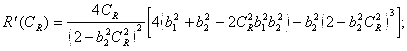
 — дельта-функция Дирака.

Для расчета кинетической энергии составлена программа на языке Паскаль. Были приняты значения параметров g=1/4; u₀=1;

v₀₌0,1c₂. При этом Н =»1,73.

В результате моделирования и обработки полученных вычислений получены требования к преобразователям ультразвуковых сигналов, их амплитудно-частотным характеристикам и соответственно к регистрирующей аппаратуре.

Список литературы:

1.Звуковое излучение двойникующих дислокаций при их выходе на поверхность / В.С. Бойко, Р.И. Гарбер, Л.Ф. Кривенко и др. // ФТТ. — 1969. — Т. 11. — С. 3624—3626.

2.Сарайкин В.А., Слепян Л.И. Плоская задача о динамике трещины в упругом теле // Изв. АН СССР. МТТ. — 1979. — № 4. — С. 54—73.

3.Синхронная регистрация перемещения дислокаций и генерируемого ими звукового излучения / В.С. Бойко, Р.И. Гарбер, В.Ф. Кившик и др. // ФТТ. — 1975. — Т. 17. — С. 1541—1543.

4.Слепян Л.И. Нестационарные упругие волны. — Л.: Судостроение, 1972. — 376 с.

5.Miller G.F., Pursey H. On the Partition of Energie between Elastic Weves in Semi — Infinite Solid // Proc. Roy. Soc. A. — 1955. — s. 223.