Статья опубликована в рамках: XII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 17 сентября 2012 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМИЗАЦИИ ТЕПЛОВОЙ ЭНЕРГИИ СИСТЕМЫ ТЕПЛОСНАБЖЕНИЯ
Мокроусов Валерий Сергеевич
аспирант, ВлГУ, г. Владимир
E-mail:
mathematical model of optimization thermal energy of heat supply system
Valeriy Mokrousov
Post-graduate student, Vladimir State University, Vladimir
АННОТАЦИЯ
В связи с повышением требований к эффективности системы теплоснабжения, важной стала проблема разработки математической модели описывающей ее оптимизацию. Разработка математической модели произведена на основании применения методов целочисленного программирования. Описана схема теплового баланса промышленного предприятия, по результатам которой разработана математическая модель оптимизации тепловых потерь. Использование полученной модели направлено на повышение качества анализа мероприятий по энергосбережению.
ABSTRACT
Due to the increasing demands for efficiency of heating system, a major problem was the development of mathematical models describing its optimization. Development of the mathematical model produced on the basis of application of integer programming. The scheme of the heat balance of the industrial enterprise was described, which resulted in the mathematical model of optimization of heat loss. The obtained results can be applied to improving the quality of analysis of energy conservation measures.
Ключевые слова: система теплоснабжения; математическая модель.
Keywords: heat supply system; mathematical model.
Постановка задачи оптимизации потребления тепловой энергии системы теплоснабжения определяется следующими положениями:
1. Объект оптимизации — система теплоснабжения промышленного предприятия (СТСПП); цель — максимальное сокращение потерь тепловой энергии путем проведения перечня организационно-технических мероприятий.
2. Ресурсы оптимизации — организационно-технические мероприятия, внедрение которых позволит снизить потери теплоэнергии или повысить энергоэффективность существующих установок.
3. Количественная оценка эффективности оптимизации выражена в количестве сэкономленной тепловой энергии в натуральном или стоимостном значении.
4. Ограничения при проведении процесса оптимизации — величина денежных средств, отпущенных на обеспечение работ по энергосбережению. При определении ограничений в ходе выполнения энергетического обследования предприятия с заказчиком дополнительно согласовываются максимальные сроки окупаемости внедряемых мероприятий.
Нахождение оптимального решения сокращения энергозатрат сводится к задачам целочисленного программирования. Результаты решения задачи оптимизации нерационального использования энергетических ресурсов могут быть представлены в виде некоторого списка организационно-технических мероприятий, выбранных тем или иным образом из общего их количества. Сами же эти мероприятия можно представить как объекты, не допускающие их дробление или декомпозицию на более мелкие части.
При поиске решения задачи оптимизации потерь энергоресурсов, необходимо учитывать наличие связей между элементами СТСПП. Это объясняется тем, что организационно-технические мероприятия, одинаковые по своему содержанию, но реализованные на различных элементах (уровнях) СТСПП, могут дать различный эффект по сокращению потерь.
Для оценки фактического состояния теплового хозяйства предприятия и разработки направлений повышения энергетической эффективности СТПП на рисунке 1 представлен принцип распределения тепловых поток на промышленном предприятии.
На основании представленной схемы (рис. 1) уравнение теплового баланса промышленного предприятия, имеет следующие формы записи:
![]() (1)
(1)
![]() (2)
(2)
 (3)
(3)
Выбор вида теплового баланса промышленного предприятия зависит от глубины и места определения потенциала энергосбережения и проработки перечня мероприятий по энергосбережению [2].
При анализе схемы теплового баланса следует обратить внимание на то, что тепловые потери присутствуют на каждой стадии, следовательно, снижение потребления тепловой энергии с помощью внедрения энергосберегающих мероприятий можно достичь при производстве, транспортировки и потребления тепловой энергии [1].
Представим постановку задачи оптимизации тепловых потерь промпредприятия с помощью комплекса взаимосвязанных математических моделей, предназначенных для решения отдельных задач (рис. 2).
По способу учета тепловой нагрузки постановку задачи оптимизации тепловых потерь системы теплоснабжения можно разделить на статическую (блок I) и динамическую (блок II). При статической постановке задачи расчетная тепловая нагрузка системы теплоснабжения задается на конечный уровень развития системы; при динамической — по годам расчетного периода.
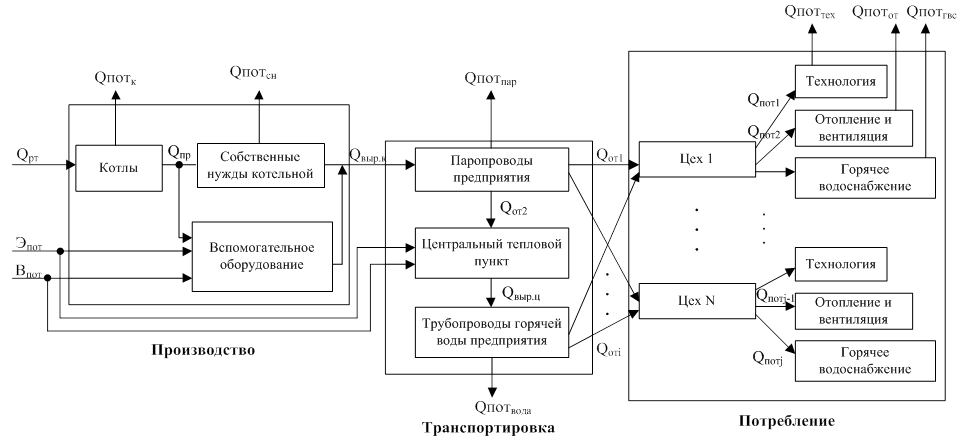
Рис.1 Схема теплового баланса промышленного предприятия.
Qрт — располагаемая теплота; Эпот, Впот — потребляемая электрическая энергия и вода для производства и передачи тепловой энергии; Qпр, Qвыр, Qот, Qпот — произведенная, выработанная, отпущенная и потребленная тепловая энергия; Qпотк, Qпотсн, Qпотпар, Qпотвода, Qпоттех, Qпотот, Qпотгвс — потери теплоты котлами, установками котельной, при передаче пара, теплофикационной воды, при технологическом процессе, в системе отопления и вентиляция, в системе ГВС.

Рис. 2 Схема решения задачи оптимизации тепловых потерь СТПП.
Общий алгоритм поиска наилучшего решения как статистической, так и динамической задачи оптимизации тепловых потерь системы теплоснабжения может быть представлен как итерационный процесс, состоящий из трех этапов: декомпозиции исходной задачи на ряд задач по числу альтернативных типов основных источников теплоснабжения (ИТ) (блок 1), далее решения каждой задачи отдельно (блок 2) с последующим сопоставлением оптимальных решений, полученных в задачах, и выбора оптимального решения задачи оптимизации структуры СЦТ (блок 3) [3].
В результате решения первой задачи определяются оптимальные трассировки транзитной и магистральной тепловой сети (ТС), места расположения и мощности ИТ; при этом используются укрупненные технико-экономические показатели ИТ. Результаты полученные в первой задаче, служат исходной информацией для второй задачи, при решении которой используются технико-экономические показатели ИТ с учетом состава их оборудования, а для ТС — диаметров трубопроводов. В результате решения второй задачи определяются оптимальные составы оборудования ИТ и диаметры трубопроводов ТС. В том случае, если технико-экономические показатели ИТ, полученные при решении второй задачи, отличаются от соответствующих укрупненных показателей первой задачи более чем на заданную величину, решение итеративно уточняется при скорректированных показателях ИТ и ТС.
На третьем этапе происходит сопоставление вариантов структур СЦТ с альтернативными типами основных ИТ и выбор оптимального варианта по критерию минимума приведенных затрат в СЦТ.
Обозначим через D множество всех мероприятий по энергосбережению. Исходное множество мероприятий D разделим на три непересекающихся множества D1, D2 и D3. Множество D1 будет включать в себя те мероприятия, которые планируются к внедрению на теплоэнергетических установках цехов, D2 мероприятия в тепловых пунктах цехов, D3 мероприятия в тепловых сетях организации.
Каждое мероприятие, рассматриваемое в задаче оптимизации энергосбережения СЭСПП имеет свою стоимость и свой эффект от внедрения, определяемый величиной снижения потерь в денежном выражении. При переходе к множествам D1, D2 и D3 предположим, что D1 содержит п мероприятий, D2 — т мероприятий, а D3 — k мероприятий. Тогда п - мерные вектора C1(i) и E1(i) содержат соответственно стоимости и эффекты мероприятий множества D1, векторы C2(i) и E2(i) — стоимости и эффекты мероприятий из множества D2, а векторы C3(i) и E3(i) — стоимости и эффекты мероприятий из множества D3. Введем также три вектора Х1(i), X2(i) и X3(i), элементы которых xi=1, если мероприятие с номером i будет выбрано для внедрения, в противном случае (мероприятие не выбрано) xi=0.
С учетом всех введенных обозначений математическая запись данной задачи имеет следующий вид:
 (4)
(4)
Предложенная математическая модель задачи оптимизации энергосбережения в СТСПП содержит две подзадачи:
1. Отбор по тем или иным признакам ЛПР энергосберегающих мероприятий — в общем случае как из множества D1, так и из множества D2 и D3 (одно или несколько из группы).
2. Решение задачи целочисленного линейного булева программирования — нахождение мероприятий, внедрение которых дает наибольший эффект.
Описанная математическая модель оптимизации тепловых потерь может быть также перенесена на модель электро- газо-, водоснабжения промышленного предприятия.
Список литературы:
1.Данилов О.Л. Энергосбережение в теплоэнергетике и теплотехнологиях: учебник для вузов. М.: Издательство МЭИ, 2011.— 424 с., ил.
2.Назмеев Ю.Г., Коназина И.А. Теплотехнические системы и энергобалансы промышленных предприятий: Учебное пособие для вузов. М.: Издательство МЭИ, 2002.— 407 с., ил.
3.Попырин Л.С. Математическое моделирование и оптимизация теплоэнергетических установок. М.: Энергия, 1978.— 416 с., ил.
дипломов


Оставить комментарий