Статья опубликована в рамках: XII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 17 сентября 2012 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
ПРЕОБРАЗОВАНИЯ СИСТЕМ КООРДИНАТ ПРИ ПОСТРОЕНИИ ПРОЕКЦИЙ ИЗОБРАЖЕНИЙ ДЛЯ РАЗЛИЧНЫХ РОТАЦИЙ КАМЕР
Лукоянов Сергей Владимирович
ассистент ФГБОУ ВПО АГТУ, г. Астрахань
E-mail:
Белов Сергей Валерьевич
канд. техн. наук, доцент, зав. кафедрой Автоматизированные системы обработки информации и управление, ФГБОУ ВПО АГТУ, г. Астрахань
TRANSFORMATIONS OF COORDINATE SYSTEM IN THE CONSTRUCTION OF PROJECTION OF IMAGES FOR DIFFERENT CAMERA ROTATION
Sergej Lukoyanov
Assistant of State Educational Institution of Higher Professional Education Astrakhan State Technical University, Asrakhan
Sergej Belov
Candidate of technical science,
head of computerized system of information processing and management,
State Educational Institution of Higher Professional Education Astrakhan State Technical University
Аннотация
В статье говориться о геометрических преобразованиях, основанные на оптических законах перспективы. Рассматриваются несколько степеней свободы движения камер, которые возможно учитывать при проектировании системы видеонаблюдения.
Abstract
The article deals with geometric transformations based on optical laws of perspective. Several degrees of free motions of cameras that may be considered by projection of video surveillance system are considered in this article.
Ключевые слова: преобразование систем координат; проецирование объектов; зоны обзора камер.
Keywords: transformation of coordinate systems; projection of objects; cameras’ coverage areas .
При проектировании объектов высокой сложности особенно трудно определить оптимальное расположение камер и взаимодействие их технических возможностей. В настоящее время на рынке существует множество калькуляторов расчетов установки камер, однако они не решают проблему выбора мест их установки и не учитывают существующий опыт, выраженный в рекомендациях Министерства внутренних дел РФ. Для создания надежной системы охраны необходимо учитывать такие характеристики, как вероятность обнаружения объекта в поле зрения камер, особенности работы камеры в ночном режиме, возможность определять точное значение затенения объектов и многие другие важные нюансы проектирования качественной системы наблюдения. Именно поэтому остается актуальной разработка системы, способной самостоятельно, безучастия человека или с минимальным его участием, с учетом огромного множества факторов и требований к установке камер, различного рода рекомендаций, основанных на опыте большого числа экспертов, утвержденных в регламентах Министерства внутренних дел РФ, размещать на объекте защиты камеры видеонаблюдения [1, с. 39—47].
Установить камеру на объекте защиты возможно во многих местах и в различных положениях. Как правило, у камеры иметься несколько степеней свободы движения, которые необходимо учитывать при проектировании. Для работы данного алгоритма необходимо математически описать процедуру перехода в различные системы координат [2, с. 28—33]. Изображение, которое видно на экранах мониторов является проекция сектора обзора камеры на матрицу камеры. Для создания модели описывающей положение камеры в пространстве необходимо выполнить следующие этапы.
1. Построение центральной проекции объекта
Для этого используются геометрические преобразования, основанные на оптических законах перспективы. Для анализа проекции объекта, как геометрической фигуры, вводиться дополнительная двумерная система координат Nuv, связанной с проецирующей плоскостью Σ, перпендикулярной оси камеры. Однако, двумерная система координат, не позволяет решать задачи, связанные с взаимным расположением нескольких объектов, в частности, задачу о закрытии одного объекта (наблюдаемого) другим (закрывающим). Для решения поставленных задач, дополнительно к осям Nu и Nv, добавляеться ось Nw, перпендикулярная осям Nu и Nv, таким образом, чтобы оси u, v и w образовывали правую систему координат. При таком построении ось w будет совпадать с прямой l — направлением оси камеры.
Направление оси камеры l зададим при помощи точки — расположения камеры и углов, задающих ротацию камеры. Координаты камеры и объектов будем задавать в глобальной пространственной системе координат Oxyz. Пусть (xc,yc,zc) — координаты камеры наблюдения C, α — угол между проекцией направления камеры l на горизонтальную плоскость и осью Ox, а β — угол между l и горизонтальной плоскостью Oxy (рис. 1).

Рис. 1: Построение центральной проекции точки A
Пусть точка N, начало системы координат, связанной с проецирующей плоскостью Σ, расположена на прямой l. Произвольному расположению точки N на прямой l соответствует определенная плоскость Σ и проекция объекта. Для простоты расчетов положим |CN|=1. Центральная проекция A′ отдельной точки A объекта на плоскость проецирования Σ определяется как точка пересечения проецирующей линии CA с указанной плоскостью:
![]()
Обозначим координаты точки A в исходной (глобальной) системе координат через (xA,yA,zA), а координаты той же точки в системе координат, связанной с проецирующей плоскостью Σ — через (uA,vA,wA).
2. Преобразования систем координат
Преобразование координат точек из глобальной системы координат (x,y,z) в локальную (u,v,w) может быть выполнено в три этапа:
1) Параллельный перенос начала координат в точку N — полученную первую вспомогательную систему координат обозначим (x’,y’,z’).
(x’,y’,z’) = (x,y,z,1) T1
где 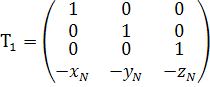 (1)
(1)
2) Вращение системы координат, полученной на первом этапе, вокруг оси z′ на угол α против часовой стрелки при наблюдении с конца оси z — полученную вторую вспомогательную систему координат обозначим (u’,v’,w’), причем оси z′ и u′ совпадают.
(u’,v’,w’) = (x’,y’,z’) T2
|
где
|
(2) |
3) Вращение системы координат, полученной на втором этапе, вокруг оси v′ на угол β против часовой стрелки при наблюдении с конца оси v′.
(u,v,w) = (u’,v’,w’) T3
|
где
|
(3) |
3. Построение матрицы преобразования
Матрица преобразования координат точек из глобальной системы координат (x,y,z) в локальную (u,v,w) может быть определена следующим образом:
(u,v,w) ![]() (u‘,v‘,w‘) T3 = ((x’,y’,z’) T2) T3 = (((x,y,z,1) T1) T2) T3 (4)
(u‘,v‘,w‘) T3 = ((x’,y’,z’) T2) T3 = (((x,y,z,1) T1) T2) T3 (4)
Используя свойство ассоциативности операции матричного умножения формула (4) может быть записана в виде:
(u,v,w) ![]() (x,y,z,1)( T1 T2 T3)
(x,y,z,1)( T1 T2 T3)
Учитывая множество вариантов расстановки камеры и ее различные степени свободы, создающие определенные ротации камеры, необходимо иметь и использовать выше приведенное математическое описание переходов в различные системы координат, которые в свою очередь зависят от выбранного место положения и направления камеры. Данное преобразование позволяет в дальнейшем построить проекцию всего объекта, в нужном виде для алгоритма проектирования расстановки камеры на объекте защиты на матрицу камеры. В дальнейшем модель проецирующих объектов на камеры в возможных местах расстановки камеры и в определенном положении, ротациях, позволит рассчитать важнейшие критерии правильности выбора данного варианта расположения камер. В том числе и критерий достаточной видимости всего объекта или его важнейших составляющих.
Список литературы:
1.Белов С. В. Попов Г.А. Оценка наблюдаемости ОЗ телекамерами на основе формирования полного набора показателей эффективности их функций . Датчики и системы № 5 — М.: ООО «СепСиДат» 2009 С. 39—47.
2.Попов Г.А., О систематизации методов поиска оптимальных решений. Вестник АГТУ. Сб. науч.трудов. Тел- ком- муникации, новые информ. Технологии и связь. Астрахань: 2000. С. 28—33.
дипломов



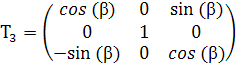
Оставить комментарий