ИССЛЕДОВАНИЕ ГЕНЕРАТОРА СЛУЧАЙНЫХ ЧИСЕЛ, РАСПРЕДЕЛЕННЫХ ПО НОРМАЛЬНОМУ ЗАКОНУ

Захарикова Елена Борисовна

аспирант, Пензенский государственный университет, г. Пенза

E-mail:

THE RESEARCH OF RANDOM NUMBER GENERATORS, DISTRIBUTED NORMALLY

Elena Zakharikova

 postgraduate student of Penza State University, Penza

АННОТАЦИЯ

В данной работе проводится исследование разработанного автором генератора случайных чисел, распределенных по нормальному закону, с помощью критерия согласия «- квадрат».

ABSTRACT

In this work the research of the random numbers distributed normally developed by the author with the goodness of fit «» is performed.

Ключевые слова: генераторы случайных чисел; закон распределения; имитационное моделирование; критерий согласия; достоверность; точность; относительная погрешность; выборка; генеральная совокупность.

Keywords: random number generators; the distribution; simulation; goodness of fit; the reliability; accuracy; relative error; sample; population.

Автором разработан пакет прикладных программ имитационного моделирования на языке С++, включающий программы для генерирования случайных величин с заданными законами распределения. Достоверность и точность результатов имитационного моделирования в значительной степени определяется качеством используемых в моделях программных генераторов псевдослучайных последовательностей.

Проверка генераторов распределенных псевдослучайных чисел предполагает формирование большой совокупности или представительной выборки случайных чисел и выполнение оценок соответствия по определенным критериям. Для статистической оценки гипотезы о том, что совокупность выборочных данных незначительно отличается от той, которую можно ожидать при некотором теоретическом законе распределения, воспользуемся критерием согласия «- квадрат» [2, с. 153]. Этот критерий позволяет проверить гипотезу, удовлетворяет ли рассматриваемая случайная величина заданному закону распределения При этом выполняются следующие этапы:

1.  Определение выборки с помощью генератора для конкретных параметров.

2.  Разбиение всего диапазона значений времени на равные интервалы (не менее 20).

3.  Определение частоты попаданий значений случайной величины в каждый интервал.

4.  Определение наблюдаемых вероятностей попаданий значений случайной величины в каждый интервал.

5.  Вычисление ожидаемых вероятностей попаданий значений случайной величины в каждый интервал.

6.  Вычисление величины  по следующей формуле:

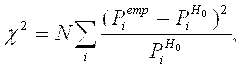
где — полный объем выборки, — наблюдаемая вероятность попадания значения в -й интервал,  — ожидаемая вероятность попадания значения в -й интервал.

Если , то практические и теоретические значения частот совпадают. Если , то полного совпадения нет, сравниваются расчетные значения  с табличными значениями. Значения статистики  табулированы для различных чисел степеней свободы и различных уровней доверительной вероятности . При практическом использовании этой статистики высказывается так называемая нулевая гипотеза о том, что между практическим и теоретическим распределением с теми же параметрами нет значительных расхождений. Если при проверке этой гипотезы расчетная величина  оказывается больше критического табличного значения (для данного уровня доверительной вероятности и соответствующего числа степеней свободы), то можно заключить, что при данном уровне доверительной вероятности наблюдаемые частоты значительно отличаются от ожидаемых, и гипотеза  отвергается.

В данной работе производится оценка функционирования разработанного генератора случайных чисел, распределенных по нормальному закону, по критерию согласия «- квадрат».

Параметры выборки: математическое ожидание случайной величины средеквадратическое отклонение , время моделирования  Рассматриваются значения случайной величины в интервале

Таблица 1.

Вычисление ожидаемых вероятностей попаданий значений случайной величины в каждый интервал для нормального распределения

Найдем критическое значение величины из таблицы [1, с. 94].

Значения наблюдаемых частот для каждого интервала должны быть не менее пяти. В противном случае смежные интервалы объединяются.

Число степеней свободы задается выражением:

где — число интервалов с учетом объединения (), — число параметров, определяемых опытным путем или на основе выборочных данных (). Таким образом, .

Табличное значение  при доверительной вероятности  равно 6.6. Следовательно, гипотеза принимается.

Таким образом, генератор нормально распределенных случайных величин функционирует корректно.

Графическая интерпретация функций плотности вероятностей эмпирического и теоретического нормального распределения (h и q соответственно) приведена на рисунке 1

Рисунок 1. Графическая интерпретация функций плотности распределения вероятностей

Соответствующие гистограммы представлены на рисунке 2

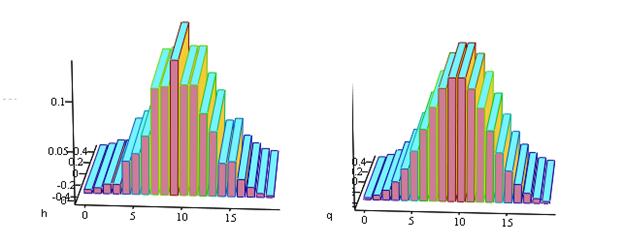
Рисунок 2. Гистограммы эмпирического и теоретического нормального распределения

Список литературы:

1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1980. — 976 с.

2. Шеннон Р. Имитационное моделирование систем. — Искусство и наука. — М.: Мир, 1978. — 418 с.