МОДЕЛЬ ТЕЧЕНИЯ ЖИДКОСТИ В ТРУБЕ

Амосов Евгений Александрович

канд. техн. наук, доцент СамГТУ, г. Самара

E-mail: amosov-ea@rambler.ru

MODEL OF THE LIQUID FLOWING IN THE PIPE

Evgeniy Amosov

Candidate Technical, Associate Professor of Samara State Tech. University, Samara

АННОТАЦИЯ

Предложена модель механической системы, являющейся аналогией жидкости, текущей в трубе. Показано, что данная модель верно отражает переход ламинарного течения в турбулентное.

ABSTRACT

A simple model of mechanical system, which is a analogy of liquid flowing in a pipe, has developed. It is shown that the model reflects the transition of a laminar flow in a turbulent.

Ключевые слова: моделирование; течение жидкости; жидкость в трубе

Keywords: modeling; liquid flowing; the liquid in the pipe

Из курса физики известно [2], что понятие вязкости было введено Ньютоном с помощью следующего мысленного опыта (рисунок 1).

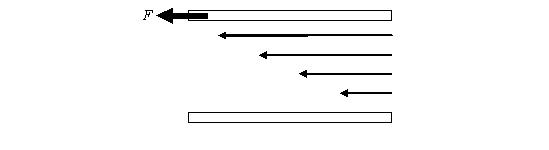
Рисунок 1 – Классический опыт Ньютона

Между двумя плоскими металлическими пластинами помещают тонкий слой жидкости. Нижняя пластина установлена неподвижно, а верхняя пластина под действием определенной силы F перемещается с постоянной скоростью. Эта сила необходима для преодоления вязких свойств жидкости.

Жидкость можно представить состоящей из очень тонких слоёв. Каждый такой тонкий слой жидкости движется с некоторой скоростью. Профиль векторов скоростей разных тонких слоев жидкости показан на рисунке 1. Такое течение жидкости принято назвать ламинарным.

Согласно представлениям Ньютона, каждый тонкий слой жидкости (если верхняя и нижняя металлические пластины имеют неограниченную протяженность в горизонтальном направлении) также имеет неограниченную протяженность в горизонтальном направлении. Проведённый автором анализ литературных данных о ламинарном течении позволяет выдвинуть гипотезу, что это не так, и каждый тонкий слой жидкости можно представить себе в виде набора плотно примыкающих друг к другу тонких пластин, движущихся вместе как один слой по другой совокупности тонких пластин или по металлической пластине.

Подобные представления позволили автору предложить следующую механическую модель – аналогию течения жидкости в трубе. Возьмём пачку тонких и плоских твердых тел, положим на стол, и будем сдвигать каждый последующий элемент пачки на малую величину по отношению к предшествующему элементу (рисунок 2).

Рисунок 2. – Модель текущей в трубе жидкости

Очевидно, что если сдвиг каждого элемента мал и количество элементов в пачке мало, то пачка не опрокинется. Опрокидывание, очевидно, произойдёт в двух случаях:

1.  пачка достаточно толстая,

2.  элементы пачки сдвигаются на достаточно большую величину.

Данная модель является аналогией ламинарного и турбулентного течения жидкости по трубе. Действительно, плоский элемент – это аналог тонкого слоя жидкости, стол – аналог стенки трубы, а высота пачки элементов – аналог радиуса трубы. Нижний элемент – аналог слоя жидкости, прилегающего к стенке трубы. Сдвиг верхнего элемента пачки пропорционален максимальной скорости движения жидкости.

Если течение ламинарное, например, в узкой трубе, то слои жидкости не перемешиваются, а скорость движения слоёв плавно возрастает от нулевой (у стенки трубы) до максимальной (в центре трубы), как показано ниже на рисунке 3.

Рисунок 3 – Распределение скорости жидкости (ламинарное течение)

Следовательно, расположение элементов на рисунке 2 напоминает реальное распределение скоростей слоёв жидкости при ламинарном течении и распределение скоростей на рисунке 1, а поэтому может считаться аналогией ламинарного течения жидкости по трубе.

Рассмотрим, как произойдёт опрокидывание пачки элементов, если выполнены указанные выше условия опрокидывания. Как показывает опыт, после опрокидывания пачки расположение элементов имеет примерно следующий вид (рисунок 4).

Рисунок 4 – Опрокинутая пачка элементов

Оставаясь в рамках нашей модели, определим, исходя из рисунка 4, что должно измениться в характере движения жидкости при переходе от ламинарного течения к турбулентному течению.

Как следует из модели, при переходе к турбулентному течению появляется вращательное движение слоёв жидкости (элементы, расположенные в правой части рисунка 4, находятся в повёрнутом положении). Кроме того, скорость некоторых слоёв жидкости (расположенных ближе к центру) выравнивается (элементы, расположенные в левой части рисунка 4, расположены одинаково). Образование разрывов между элементами (в правой части рисунка 4) говорит о возможном образовании пузырьков в жидкости при её турбулентном течении.

Сравним наши предположения с реальным турбулентным течением жидкости в трубе. Как известно, при турбулентном течении распределение скорости имеет следующий вид (рисунок 5).

Рисунок 5 – Распределение скорости жидкости (турбулентное течение)

Как видно из рисунка 5, действительно, скорости слоёв в средней части трубы выравниваются по сравнению со случаем ламинарного течения. Кроме того, турбулентное течение также называют вихревым движением жидкости, то есть в таком движении присутствует вращение, как это и следует из нашей модели.

Как известно, турбулентное течение может сопровождаться появлением пузырьков (или разрывов) в жидкости. Поэтому выводы, вытекающие из нашей модели, в принципе согласуются с реальным поведением жидкости при её турбулентном течении.

Определим, согласуется ли наша модель с представлениями о том, что переход ламинарного течения в турбулентное происходит, если число Рейнольдса, характеризующее движение жидкости, превысит некоторое критическое значение. Как известно [1], число Рейнольдса равно

Re=V∙L∙ρ/μ,                                                        (1)

где V – характерная скорость течения жидкости, L – характерный размер трубы (как правило, диаметр), ρ – плотность жидкости, μ – коэффициент вязкости жидкости. То есть, согласно этому критерию, движение жидкости станет турбулентным при большой скорости течения жидкости или большом размере трубы или при следующем условии (если жидкость одна и та же, то есть вязкость и плотность жидкости не изменяются)

V∙L>(V∙L) _крит.                                                     (2)

Как уже было отмечено, в нашей модели опрокидывание пачки происходит, если пачка достаточно толстая (или радиус трубы, пропорциональный толщине пачки, достаточно большой) или если сдвиг элементов пачки     достаточно большой (или скорость течения жидкости, пропорциональная сдвигу элементов пачки, достаточно большая). Таким образом, согласно нашей модели, переход ламинарного течения в турбулентное должен произойти при большой скорости течения жидкости или большом радиусе трубы, то есть если произведение V∙L превысит некоторое критическое значение, что полностью согласуется с рассмотренным выше условием турбулентности (2).

Таким образом, наша модель, несмотря на явное упрощение процесса течения жидкости в трубе, качественно верно отражает некоторые особенности течения жидкости. Поэтому данная модель вполне может быть использована как простая и наглядная аналогия процесса перехода ламинарного течения жидкости в турбулентное течение при её движении по трубам.

Список литературы:

1.Биркгоф Г. Гидродинамика. Методы. Факты. Подобие. М.: Иностранная литература, 1963. 246 с.

2.Лойцанский Л.Г. Механика жидкости и газа. М.: Наука, 1970. 904 с.