Статья опубликована в рамках: VII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 13 марта 2012 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ ДИНАМИКИ ГАЗОВ В МНОГОСТУПЕНЧАТЫХ КАНАЛАХ ТЕПЛО – И МАССООБМЕННЫХ АППАРАТОВ
Исмаилов Бахтияр Рашидович
д-р техн. наук, профессор ЮКГУ им. М. Ауезова, г. Шымкент
Исмаилов Хайрулла Бахтиярович
канд. техн. наук, доцент ЮКГУ им. М. Ауезова, г. Шымкент
Урматова Айжан-
докторант МКТУ им. Х. А. Яссави, г. Шымкент
E-mail: ismailb@mail.ru
Контактные устройства колонных технологических аппаратов системы «газ-жидкость» с регулярными насадками имеют различные конструкции, которые соответствуют требованиям реализуемых процессов. В них потоки газа и жидкости подвергаются многоступенчатой обработке, соответствующей количеству насадок в форме пластин, цилиндров, сфер и т. д. Поэтому, естественным названием таких контактных устройств аппаратов является «многоступенчатые каналы» (МСК). Различаются также соответствующие математические модели, описывающие гидродинамические и тепломассообменные процессы. Однако основные закономерности динамики потоков в каналах разных форм могут быть описаны одними и теми же уравнениями (Навье-Стокса в ламинарном режиме и Рейнольдса - в турбулентном). Геометрия МСК определяется граничными условиями на элементах насадок, стенках аппарата и схемой взаимного расположения этих элементов. Имеется большое количество работ по моделированию течения газа в каналах сложной формы, в которых исследована динамика потоков в массообменных аппаратах, влияние динамических характеристик на тепло- и массообмен. На наш взгляд, приемлемыми с точки зрения технических приложений и реализации численными методами являются подходы, разработанные в [1] (ламинарный режим) и [2] (турбулентный режим).
В настоящей работе вышеназванные методики нахождения динамических характеристик конкретизированы для случая МСК.
Длина большинства каналов с многоступенчатым взаимодействием фаз эксплуатируемых в настоящее время колонных массообменных аппаратов велика и сквозной расчет динамических характеристик численными методами требует очень большого объема памяти компьютера и времени счета. Из-за многократного повторения вычислительных процедур при этом происходит накопление погрешностей округления, что в конечном итоге может привести к искажению конечного численного решения. Для решения этой проблемы нами использован следующий прием, который можно назвать принципом гидродинамического установления, известный для прямых цилиндрических труб: профиль скорости, заданный на входе в канал (например, прямоугольный или параболический), развиваясь по течению, через определенное расстояние достигает такой формы, которую можно считать установившейся. Этот прием вписывается в рамки идеи о представлении аппарата как совокупности нескольких каналов. Для МСК, для которых нами проведены расчеты динамических характеристик газового потока, принцип установления означает следующее [3] (рис. 1):
- Пусть
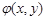 - одна из динамических характеристик в многоступенчатом канале (функция тока, завихренность
- одна из динамических характеристик в многоступенчатом канале (функция тока, завихренность 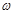 , кинетическая энергия
, кинетическая энергия 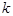 и масштаб турбулентности
и масштаб турбулентности 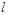 ). Обозначим через
). Обозначим через 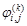 ее значения в узлах конечно-разностной сетки в момент времени
ее значения в узлах конечно-разностной сетки в момент времени 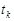 . На входе в МСК задаем значения
. На входе в МСК задаем значения 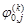 , определяющие форму входного профиля. На других сечениях разностной сетки в начальный момент времени задавали такие значения динамических функций, которые обеспечивали постоянство расхода по всем горизонтальным сечениям канала.
, определяющие форму входного профиля. На других сечениях разностной сетки в начальный момент времени задавали такие значения динамических функций, которые обеспечивали постоянство расхода по всем горизонтальным сечениям канала. - Проводится одна итерация по соответствующей формуле расчета и находятся
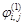 для одной ступени контакта.
для одной ступени контакта. - Для продолжения итерации во второй ступени контакта значения
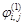 при i=n(на выходе из 1-ступени контакта) передаются значениям
при i=n(на выходе из 1-ступени контакта) передаются значениям 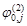 для 2-ступени контакта.
для 2-ступени контакта. - Находятся значения
 для второй ступени контакта.
для второй ступени контакта. - Если значения
 для двух следующих друг за другом ступеней контакта совпадают с заданной точностью, то итерации заканчиваются, и значения
для двух следующих друг за другом ступеней контакта совпадают с заданной точностью, то итерации заканчиваются, и значения 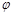 на последней ступени контакта могут быть приняты за установившиеся значения динамических характеристик на стабилизированном участке канала.
на последней ступени контакта могут быть приняты за установившиеся значения динамических характеристик на стабилизированном участке канала.
Таким образом, всю длину МСК можно представить как совокупность начального и стабилизированного участков, причем длина стабилизированного участка оказывается гораздо больше длины начального участка. Такой эффект установления известен для цилиндрических труб: входной профиль скорости, развиваясь по течению, устанавливается через определенное расстояние от входа, приобретая форму параболы, т. е. реализуется течение Пуазейля. Длина начального участка зависит от формы входного профиля (прямоугольная, трапециевидная, параболическая и т. д.).
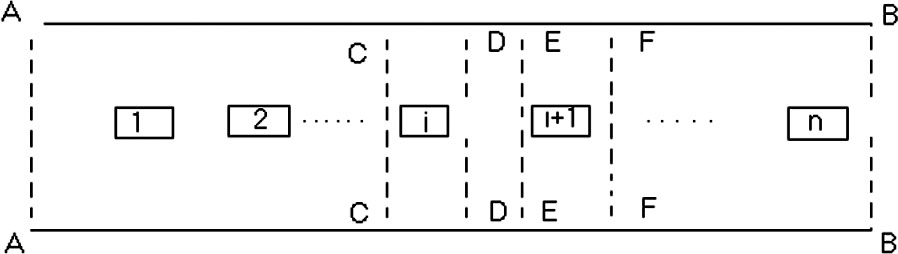
Ось абцисс - продольное направление, ось ординат - поперечное направление к потоку, 1,2,…,n- обтекаемые элементы.
Рис. 1. Схематическое изображение обтекания газом насадок в МСК.
В существующих тепло- и массообменных аппаратах могут использоваться не один, а несколько рядов параллельно установленных насадок, поэтому при моделировании течений в них необходимо учитывать взаимное влияние нескольких потоков. Этот эффект моделируется соответствующими граничными и начальными условиями, а также с условиями сопряжения:
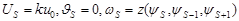 , (1)
, (1)
где 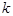 - коэффициент уменьшения, зависящий от разброса общего расхода газа;
- коэффициент уменьшения, зависящий от разброса общего расхода газа; 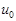 - среднерасходная скорость газа; -функция тока; S - кривая, которую можно считать линией симметрии между двумя рядами потоков, обтекающих 2 ряда элементов насадок или границей стенки канала;
- среднерасходная скорость газа; -функция тока; S - кривая, которую можно считать линией симметрии между двумя рядами потоков, обтекающих 2 ряда элементов насадок или границей стенки канала; 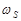 - значение завихренности на разделительной линии;
- значение завихренности на разделительной линии; 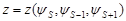 - функция, в общем случае получаемая трехточечной аппроксимацией граничного условия для функции завихренности:
- функция, в общем случае получаемая трехточечной аппроксимацией граничного условия для функции завихренности:
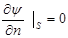 (2)
(2)
Уравнения Навье-Стокса в переменных Гельмгольца 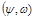 , моделирующие течение газа в МСК имеют следующий вид:
, моделирующие течение газа в МСК имеют следующий вид:
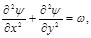 (3)
(3)
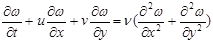 , (4)
, (4)
где 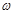 -функция напряженности вихря;
-функция напряженности вихря; 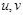 -компоненты вектора скорости по продольному и поперечному направлениям,
-компоненты вектора скорости по продольному и поперечному направлениям, 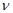 - коэффициент вязкости, t - время. Граничными условиями для функций тока и завихренности (в неявном виде) являются
- коэффициент вязкости, t - время. Граничными условиями для функций тока и завихренности (в неявном виде) являются
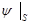 =const, (5)
=const, (5)
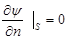 (6)
(6)
На рис. 2 приведено распределение продольной составляющей скорости в стабилизированном участке МСК с элементами насадки в виде неподвижных пластин, полученное численным решением (3)—(6) в безразмерных переменных. Результаты показывают, что в непосредственной близости от кромки пластины скорость достигает максимальных значений, а также возникают отрицательные значения скорости до и после пластины (вихрь).

Re=200; х – расстояние между насадками: 1-х=0,2; 2-х=0,8; у– расстояние от левой стенки либо разделяющей линии.
Рис.2. Продольная составляющая скорости газа в МСК с регулярными пластинчатыми насадками в стабилизированном участке.
Для учета влияния турбулентности фаз на интенсивность процессов переноса необходимо использование методов теории турбулентности. Нами используется метод Патанкара-Сполдинга [3, 4]. В декартовой системе координат
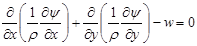 , (7)
, (7)
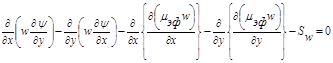 , (8)
, (8)
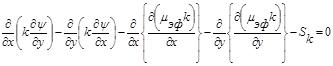 , (9)
, (9)
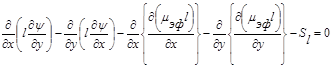 . (10)
. (10)
Особенностью уравнений (7)—(10) является их единая форма записи, которая дает возможность разработать универсальный алгоритм их численного решения. Отличительные свойства динамических функций отражают источниковые члены 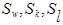 . Приведем их выражения в декартовой системе координат:
. Приведем их выражения в декартовой системе координат:
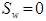 , (11)
, (11)
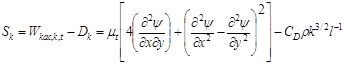 , (12)
, (12)
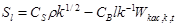 , (13)
, (13)
 . (14)
. (14)
Для использования математической модели (7)—(14) для расчета динамических характеристик в МСК с другими формами насадочных элементов необходимо ставить соответствующие начальные и граничные условия, описывающие геометрию насадок, а также выбрать значения констант 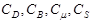 .
.
Список литературы:
- Госмен А. Д., Пан В. М., Ранчел А. К. и др. Численные методы исследования течений вязкой жидкости. - М.: Мир, 1972. – 324 с.
- Пасконов В. М., Полежаев В. И., Чудов Л. А. Численное моделирование процессов тепло- и массообмена. - М.: Наука, 1984. – 284 с.
- Kholpanov L. P., Ismailov B. R., Balabekov O. S. Distrubution of Gas Flow parameters in mass transfer columns with regularly spaced shelves // Theoretical foundations of chemical engineering. Vol.36, № 5, 2009. pp. 409—413.
- Kholpanov L. P., Ismailov B. R., Vlasec P. Modelling of multiphase flow containing bubbles, drops and solid particles //Engineering mechanics 2005. Vol. 12, № 6, p. 1—11.
дипломов


Оставить комментарий