МЕТОДИКА ЛИНЕАРИЗАЦИИ УРАВНЕНИЙ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА

Гулай Татьяна Александровна

доцент, канд. техн. наук, доцент СГАУ, г. Ставрополь

E-mail:

Литвин Дмитрий Борисович

доцент, канд. техн. наук, доцент СГАУ, г. Ставрополь

E-mail: litvin-372@yandex.ru

Линеаризация системы нелинейных уравнений пространственного движения самолета выполняется обычно после искусственной декомпозиции его на продольное и боковое в окрестности прямолинейного равномерного горизонтального полета. При этом линеаризация движения в окрестности некоторой заданной пространственной траектории практически не рассматривается и представляется громоздкой и не прозрачной процедурой.

В предлагаемой работе делается попытка устранить указанный пробел на примере динамических уравнений поступательного движения путем использования формального матричного подхода.

Нелинейные динамические уравнения пространственного движения самолета как твердого тела в векторной форме имеют вид [1]:

,

которые в проекциях на оси связанной системы координат  [2] с использованием матричного исчисления запишем в форме:

.           1

Здесь использованы следующие обозначения:

- векторы земной скорости, тяги двигателей и силы тяжести, заданные в проекциях на оси связанной  СК;

- вектор аэродинамической силы, заданный в скоростной СК;

 - вектор угловой скорости самолета, заданный в связанной СК,

и кососимметрическая матрица из его компонентов;

 - матрицы перехода к связанной СК от скоростной  и нормальной  СК [2] соответственно, которые представляют собой произведения матриц элементарных поворотов вида 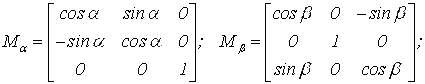[2]:

                      2

Для линеаризации уравнений воспользуемся методом малых отклонений, суть которого заключается в следующем.

Рассчитывается опорное (невозмущенное) движение, для которого векторы состояния, управления и возмущения становятся известными функциями времени . Далее записываются исходные нелинейные уравнения, описывающие данное опорное движение:

                                  3

Затем всем параметрам опорного движения придаются малые приращения для получения возмущенного движения:

.                      4

Поскольку возмущенное движение 4 мало отличается от опорного 3, то его можно с достаточно высокой точностью разложить в ряд Тейлора с сохранением лишь линейных членов, а затем вычесть из него опорное движение. Получим:

;

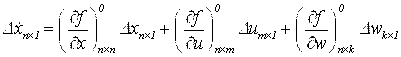,                5

где 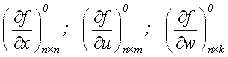 - матрицы первых частных производных (матрицы Якоби) соответствующих размерностей. Матрицы Якоби вычис­ляются на опорном движении , что обозначено индексом «о». Уравнение 5  называется линеаризованным уравнением.

Используя рассмотренную выше методику, линеаризованное в окрестности заданной пространственной траектории матричное уравнение 1  примет вполне обозримый вид:

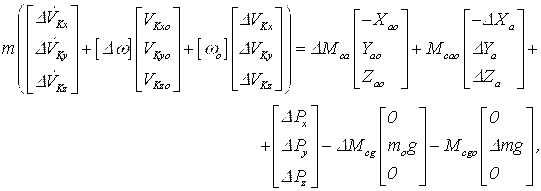       6

где  - матрица приращения матрицы  вида:

,     7

,

8

.                                                          9

Матрица , определяется по аналогии с выражениями 7— 8.

Линеаризованные для общего случая пространственного движения уравнения сил примут вид:

 ;

.

Теперь рассмотрим наиболее распространенный частный случай пространственного движения - равномерный прямолинейный горизонтальный полет, для которого характерны следующие значения параметров:

 10

В этом случае опорная фазовая траектория вырождается в точку фазового пространства, а модель движения становится стационарной. При этом все матрицы поворота становятся единичными

,                              11

а матрицы приращений 2, 8  приобретают наиболее простой вид:

 ,

.  12

Учитывая выражения 10, уравнения движения 6  примут вид: 

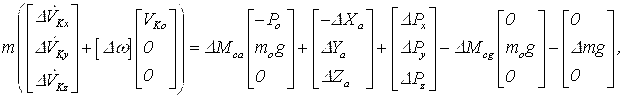                  13

а с учетом выражений 11—13  еще более простой и окончательный вид:

 .

Таким образом, использование предложенного матричного подхода придает большую компактность и наглядность процессу линеаризации уравнений пространственного движения самолета в окрестности заданной траектории.

Список литературы:

1.Вавилов Ю. А. Системы автоматического управления полетом. Учебник для курсантов и слушателей ВУЗов ВВС. М.: ВВИА им. проф. Н. Е. Жуковского, 2010 г. 495 с.

2.ГОСТ 20058-80 Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения. 52 с.