Статья опубликована в рамках: VI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 13 февраля 2012 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ ПЛАСТИЧЕСКОГО ТЕЧЕНИЯ ПРИ РЕЗАНИИ
Аверьянова Инна Олеговна
канд. техн. наук, доцент МГИУ, г. Москва
Одним из перспективных направлений развития науки о резании металлов является использование достижений теории пластичности. Основанием для применения теории пластичности служит то, что превращение срезаемого слоя в стружку происходит в пластической зоне. Причем в пластической зоне сложной формы с высокоградиентным неравномерным распределением напряжений, деформаций, скоростей деформаций и температуры. Многие исследователи пытались применять методы теории пластичности для анализа процесса резания. Наибольшее количество исследований выполнено с использованием метода линий скольжения, в рамках которого, к сожалению, может быть использована только идеальная жестко-пластическая модель обрабатываемого материала [2]. Аналогичным недостатком обладает энергетический метод, который применен в работе [1]. Методы анализа пластического течения в зоне стружкообразования, которые применены в работах [1, 2] относятся к приближенным инженерным методам и не позволяют ответить на целый ряд важных для теории и практики вопросов и дать количественную и достоверную оценку таких параметров как влияние угла резания силу резания, величину усадки стружки, влияние радиуса режущей кромки резца на указанные параметры, а также их влияние на глубину наклепанного слоя обработанной поверхности и др.
Ответы на эти вопросы могут быть найдены только на основе анализа локальных характеристик напряженно-деформированного состояния в каждой материальной точке области стружкообразования, полученных путем использования для расчетов реологических моделей обрабатываемых материалов адекватно отражающих их реальные свойства. К локальным характеристикам относятся данные о напряжениях, деформациях, скоростях деформаций и температуре. Одним из наиболее широко применяемых инструментов для исследования локальных характеристик напряженно-деформированного состояния (НДС) в пластической области является метод конечных элементов, который реализован в известных программных продуктах мирового уровня QFORM, FORGE, DEFORM, SUPERFORG/SUPERFORM, LS DYNA, ANSIS. Перечисленные программные продукты позволяют с высокой точностью произвести расчет сил резания, работы сил резания, усадки стружки, конфигурации и площади контактной поверхности с инструментом и границ пластической зоны, распределение давлений на поверхности инструмента, полей напряжений, деформаций, скоростей деформаций и температур в зоне стружкообразования и в инструменте.
В настоящей работе были произведены виртуальные и физические экспериментальные работы по резанию латуни Л60. Физические эксперименты проводили с целью последующей проверки адекватности принятой модели. Сопоставление результатов физического и виртуального экспериментов проводили сопоставлением интегральной характеристики процесса: силы резания, а также сопоставления кинематики течения металла в зоне резания, полученной в результате обработки экспериментальной координатной сетки и расчетной лагранжевой сетки, полученной моделированием процесса в DEFORM.
Для физического и виртуального экспериментов назначалась скорость резания ![]() = 0,4 мм/с при толщине срезаемого слоя а=0,15 мм и передних углах резца
= 0,4 мм/с при толщине срезаемого слоя а=0,15 мм и передних углах резца ![]() равных -5, +8, +17 и +39 градусов.
равных -5, +8, +17 и +39 градусов.
Для виртуальных экспериментов была задана реологическая модель обрабатываемого материала в виде зависимости напряжения текучести ![]() от степени деформации
от степени деформации ![]() , скорости деформации
, скорости деформации ![]() и температуры T:
и температуры T:
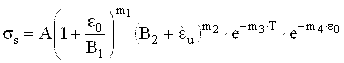 , (1)
, (1)
где А=217,176; В1=0,01; В2=0,008; m1=0,3; m2 =0,015; m3 =0,002; m4=0,01.
Аппроксимация (1) была получена в соответствии с экспериментальными данными для латуни Л60, приведенными в работе [3].
Использованный материал заготовки – упруго пластический с модулем упругости Е=98000 МПа, с пределом прочности![]() =350 МПа и
=350 МПа и ![]() =110 МПа, относительное удлинение при разрыве
=110 МПа, относительное удлинение при разрыве ![]() =0,4; толщина срезаемого слоя 0,15 мм, ширина срезаемого слоя 3 мм, резец – абсолютно жесткий, радиус округления режущей кромки – 0,02 и 0,05 мм; коэффициент трения – 0,1. Предполагалось плоское деформированное состояние. начальная температура – 200С; коэффициент теплопроводности – 108,8
=0,4; толщина срезаемого слоя 0,15 мм, ширина срезаемого слоя 3 мм, резец – абсолютно жесткий, радиус округления режущей кромки – 0,02 и 0,05 мм; коэффициент трения – 0,1. Предполагалось плоское деформированное состояние. начальная температура – 200С; коэффициент теплопроводности – 108,8 ![]() ; коэффициент теплопередачи в зоне контакта – 40
; коэффициент теплопередачи в зоне контакта – 40 ![]() ; температура стока - 20
; температура стока - 20![]() ; коэффициент теплопередачи в окружающую среду (воздух) - 0,4
; коэффициент теплопередачи в окружающую среду (воздух) - 0,4 ![]() . Предположение о плоском деформированном состоянии принято на том основании, что отношение ширины срезаемого слоя 3 мм к его толщине 0,15 мм составляет существенно более 6, при котором принимается указанное предположение.
. Предположение о плоском деформированном состоянии принято на том основании, что отношение ширины срезаемого слоя 3 мм к его толщине 0,15 мм составляет существенно более 6, при котором принимается указанное предположение.
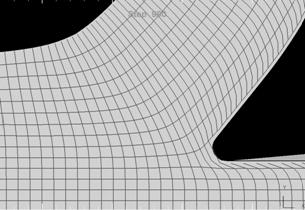
Результаты физического и виртуального моделирования кинематики течения на установившейся стадии течения металла при резании приведены на рис. 1.

|
|
|
Рис. 1. Деформированная сетка при строгании резцом с передним углом 39о:
а – физический эксперимент; б – моделирование (виртуальный эксперимент)
Продольные линии координатной сетки представляют собой в данном случае траектории перемещения частиц металла. В нашем исследовании производилось сопоставление траекторий перемещения узловых точек экспериментальной и расчетной (полученной в результате виртуального эксперимента) координатных сеток. Измерение координат узловых точек производилось по методике, изложенной в работе [4]. Начало координат было выбрано на пересечении линий, определяющих переднюю и заднюю поверхности резца. Среднестатистическое отклонение координат узловых точек полученных экспериментально и расчетным путем составило 5—7 %, что подтверждает удовлетворительное совпадение экспериментальных и расчетных результатов
Далее было произведено сопоставление экспериментальной и расчетной величины силы резания. Физический эксперимент по определению силы резания производили при строгании пластин толщиной 3 мм, закрепленных на столе фрезерного станка. Резец устанавливали в динамометре, зафиксированном на станине станка. Толщину среза 0,15 мм контролировали индикатором и измеряли на фотографии корня стружки. Таким образом, размеры срезаемого слоя составляли: толщина 0,15 мм, ширина 3 мм. По показаниям индикатора динамометра сила резания составила 702—708 Н.
При проведении виртуального эксперимента в программном комплексе DEFORM расчет производился с установленной по умолчанию для всех процессов плоской деформации единичной толщиной заготовки. Зависимость силы резания от времени протекания процесса, полученная в DEFORM, показана на рис. 2.

Рис. 2. Зависимость силы резания от времени (подачи)
Среднее расчетное значение силы резания на установившейся стадии, как видно из рис. 2, составило 230 Н. Экспериментальное значение равное 702—708 Н, приведенное к единице ширины срезаемого слоя, составило 234—236 Н, т. к. ширина срезаемого слоя была 3 мм. Некоторое превышение экспериментальной величины связано с колебаниями силы в процессе резания и осциллирующей реакцией стрелки индикатора динамометра на колебания силы. Таким образом, расчетные и экспериментальные данные практически совпали, что свидетельствует о хорошей сходимости результатов физического и виртуального экспериментов. Дополнительно было произведено сравнение силы резания, рассчитанной в DEFORM с результатами расчета по инженерной методике [2]. Сила резания, рассчитанная по методике [2] составила для резцов с различными величинами переднего угла от 260 до 280 Н, что дает ошибку до 20 % по сравнению с экспериментальными данными.
Конечноэлементное моделирование позволяет установить целый ряд важных технологических параметров, которые другим путем установить трудно или невозможно. В частности, непосредственным измерением модели может быть установлена толщина стружки в пластической зоне. Например, непосредственным измерением получена длина линии среза L=0,640209 на рис. 3.
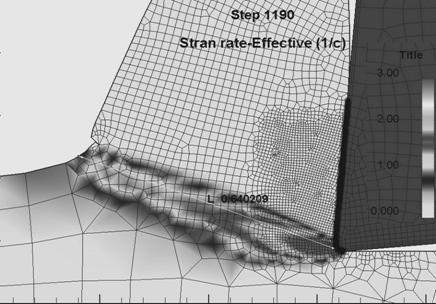
Рис. 3. Распределение интенсивности скоростей деформации в пластической области при резании резцом с передним углом 8о
Усадка стружки может быть получена для заданной марки материала в виде функции переднего угла, условий трения на контакте между заготовкой и инструментом и др. параметров при необходимости оптимизации по какому–либо параметру процесса. Аналогичные данные могут быть получены для уже упоминавшейся выше силы резания, площади контактной поверхности, след которой показан на рис. 3 в виде жирной черной линии, прилегающей к контуру резца.
Интересные данные можно получить о глубине наклепанного слоя под поверхностью обработанной детали на основе полей Stress-Effective (рис. 4, 5), в нашей терминологии интенсивности напряжений. На рис. 4 граница между серой и синей областью является границей между упругой и пластической областями. Данные, приведенные на рис. 4 и 5, показывают, что глубина наклепанного слоя существенно зависит от величины переднего угла резца. При резании с углом 8о наклепанный слой составляет ![]() 0,19 мм, а с углом 39о около 0,058 мм.
0,19 мм, а с углом 39о около 0,058 мм.
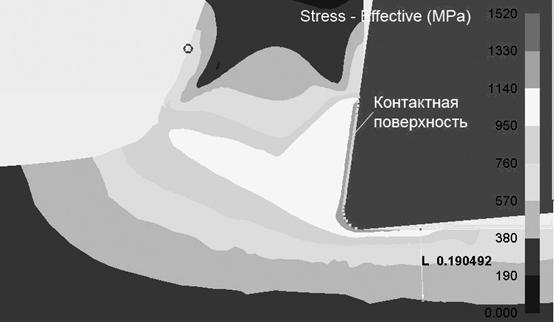
Рис. 4. Распределение интенсивности напряжений (Stress-Effective) в пластической области при резании резцом с передним углом 8о
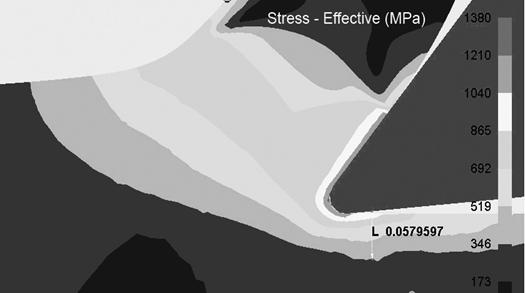
Рис. 5. Распределение интенсивности напряжений (Stress-Effective) в пластической области при резании резцом с передним углом 39о
Таким образом, используемые в качестве входной информации данные, адекватно отражающие основные механические и теплофизические свойства обрабатываемого материала, при конечноэлементном моделировании позволяют существенно расширить объем сведений о поведении материала при резании, его функциях отклика на воздействие режущего инструмента, произвести оценку влияния различных параметров резания на его силовые параметры, на свойства обработанной поверхности, на свойства и геометрию удаляемых объемов материала.
Список литературы:
1.Воронцов А. Л., Султан-Заде Н. М. Теоретические основы деформированного состояния поверхностного слоя и параметра точности деталей машин при изготовлении резанием // СТИН, № 3, 2010. с. 31—36.
2.Петрушин С. И., Проскоков А. В. Стружкообразование с развитой зоной пластических деформаций при резании материалов // Изв. Томского политехнического университета. - 2009, Т. 314, № 2, с. 57—62.
3.Полухин П. И., Гун Г. Я., Галкин А. М. Сопротивление пластической деформации металлов и сплавов: Справочник. – М.: Металлургия, 1976. –488 с.
4.Шестаков Н. А. Расчеты процессов обработки металлов давлением в Mathcad. Решение задач энергетическим методом. М., МГИУ, 2008, – 344 с.
дипломов


Оставить комментарий