Статья опубликована в рамках: V Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 12 декабря 2011 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
ОЦЕНКА ПРИМЕНИМОСТИ РАСЧЕТНЫХ МОДЕЛЕЙ ВИХРЕВОГО ПОТОКА
Мальцев Андрей Викторович
начальник производства, НПП«Доза», г. Зеленоград.
При проведении опытно-конструкторских работ при разработке любых систем и, в частности, вихревых расходомеров, требуется математический аппарат, позволяющий оценить характеристики проектируемых изделий. На текущий момент времени вопрос о поведении вращающегося потока сжимаемой среды в трубопроводе рассматривается на уровне общих рекомендаций. В связи с этим вопрос о необходимости создания модели, позволяющей получить пригодные для практических целей данные, а также оценить влияние таких эффектов, как образование буферного слоя, влияние потерь вращательного момента импульса, и т. п. является актуальным.
Для начала рассмотрим установившийся процесс вращения цилиндрического объема сжимаемой среды. В качестве расчетной модели возьмем цилиндр радиусом R0, высотой H0, заполненный газом плотностью r0 при давлении Р0. Цилиндр вращается с установившейся скоростью w при постоянстве температуры во всех точках цилиндра. Т. е. данное состояние является установившимся и в объеме отсутствуют какие-либо процессы тепло-массообмена.
Выделим элемент объема, представляющий цилиндр радиусом r и толщиной Dr. Давления P1 и P2, действующие на внутреннюю и внешнюю поверхности выделенного объема связаны соотношением:
![]() (1)
(1)
где:
 (2)
(2)
DP - приращение давления, вызванное действием центробежных сил на газ, заключенный в рассматриваемом объеме,
P(r) - функция, описывающая распределение давления по радиусу цилиндра (считаем рассматриваемый газ идеальным, для которого справедливо уравнение Менделеева-Клайперона).
Интегрируя уравнение (2) получаем:
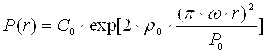 (3)
(3)
где коэффициент С0 суть давление в центральной части вращающегося объема.
Считаем, что в рассматриваемом объеме заключен газ массой m. Тогда для покоящегося цилиндра справедливо:
![]() (4)
(4)
для вращающегося:
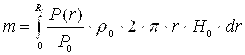 (5)
(5)
Интегрируя (5) получаем:
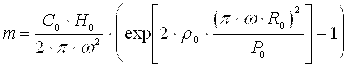 (6)
(6)
Приравняв (2.5), (2.7) и выразив С0, получаем:
 (7)
(7)
Подставив (2.8) в (2.4) получаем:
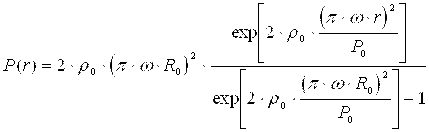 (8)
(8)
Для удобства чтения введем обозначение:
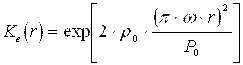 (9)
(9)
Рассмотрим вихреобразующую камеру. В качестве модели возьмем систему, состоящую из N подводящих каналов, одна из стенок которых касательна к образующей окружности камеры радиусом R0 (рисунок 1).
|
|
|
Рисунок 1. Модель, используемая при расчете момента импульса входящей в вихреобразующую камеру среды. а) общий вид камеры; б) выделенный элемент объема. |
Считаем, что в связи с малой протяженностью каналов профиль скорости потока в них линеен и связан с объемным расходом следующим соотношением:
 (10)
(10)
где: Vk - линейная скорость потока в подводящем канале (см/с);
VV - объемный расход (л/мин);
Hk - высота вихреобразующей камеры (см);
Yk - ширина канала (см);
N - количество каналов.
При этом указанная скорость для каждого элементарного объема на границе вихреобразующей камеры может быть представлена как сумма тангенциальной и радиальной составляющих (рисунок 1) и выраженных:
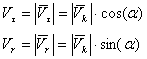 (11)
(11)
при этом:
 (12)
(12)
что очевидно.
Момент импульса рассматриваемого объема относительно центра симметрии равен:
 (13)
(13)
В уравнении (13) применена подстановка: ![]() , что позволяет использовать понятие: “импульс, пришедший в объем камеры за время Dt”. Интегрируя уравнение (13) по ширине канала получаем:
, что позволяет использовать понятие: “импульс, пришедший в объем камеры за время Dt”. Интегрируя уравнение (13) по ширине канала получаем:
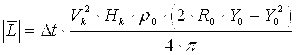 (14)
(14)
для одного канала. Для N каналов - соответственно в N раз больше, поскольку моменты импульсов имеют одинаковое направление вращения.
Перейдем к задаче нахождения частоты вращения вихря в формирующем патрубке. Для несжимаемой среды распределение массы по радиусу равномерно и, следовательно, можно записать для момента импульса, прошедшего через какое-либо сечение формирующего патрубка за время Dt следующее выражение:
![]() (15)
(15)
Приравняв (15) и (14) получаем:
 (16)
(16)
где w - искомая частота вращения.
Как видно из соотношения (16) частота вращения несжимаемой среды линейно зависит от ее скорости на входе в вихреобразующую камеру.
Для сжимаемой среды, распределение давления по радиусу вращающейся структуры которой описывается уравнением (8) справедливо:
 (17)
(17)
Интегрируя (17) с учетом (8), (9) и учитывая, что линейная скорость сформированной вихревой структуры равна:
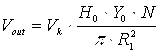 (18)
(18)
где R1 - радиус формирующего патрубка.
получаем:
 (19)
(19)
Система уравнений (14) и (19) решается численным методом.
Уравнение (19) выведено без учета влияния пограничного слоя на рассматриваемую систему. Очевидно, для вихревой структуры под пограничным слоем следует понимать область, в которой происходит прекращение вращательного движения, в то время как для поступательного движения это пристеночная область, в которой скорость потока снижается до нуля. В связи с этим можно рассматривать поток в формирующем патрубке как совокупность центральной вращающейся области, в которой распределение давления описывается уравнением (8) и периферийной части, давление в которой равномерно и определяется давлением на периферии вихревой структуры. Исходя из этого предположения найдем момент импульса такой системы.
Первоначально определим давление в центральной области вихря (C0 в уравнении (8)), для этого найдем массы газов, заключенные в центральной и периферийной областях.
Центральная область (уравнение (6)):
![]()
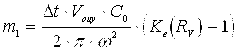 (20)
(20)
где RV - радиус вихревой структуры.
Периферийная область:
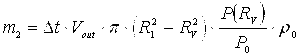 (21)
(21)
Суммарная:
![]() (22)
(22)
Приравняв (22) к сумме (20) и (21) выразим C0:
 (23)
(23)
Аналогично выводу (19) получим уравнение для момента импульса рассматриваемой структуры (с учетом нового коэффициента С0 и верхнего предела интегрирования RV):
 (24)
(24)
Видно, что при RV равном R1 уравнение (24) преобразуется в (19).
Полученное уравнение связывает момент импульса системы не только с геометрическими параметрами системы и скоростями среды, но и с толщиной пограничного слоя для вихревой формации без учета потерь на преодоление сил вязкостного трения, которые и обуславливают наличие этого слоя. В литературе [1, с. 264] для нахождения толщины пограничного слоя как ламинарного, так и турбулентного течения в трубе предлагается следующая зависимость:
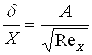 (25)
(25)
где: d - толщина пограничного слоя;
X - расстояние от края трубы;
A - постоянный коэффициент;
Rex - число Рейнольдса (в качестве характеристического размера предлагается брать расстояние X).
Так как при выводе данного уравнения скорость, входящая в число Рейнольдса, рассматривалась как основной фактор, приводящий к диссипации энергии, то логично при использовании данного уравнения учитывать как поступательную, так и вращательную составляющие скорости. Таким образом, уравнение (25) можно преобразовать:
 (26)
(26)
где u - кинематическая вязкость воздуха.
Значение коэффициента А, приведенные в литературе, изменяются от 5 при обтекания ламинарным потоком плоской пластины до 0.3 в случае турбулентного течения жидкости в трубопроводе и представляет интенсивность роста толщины пограничного слоя.
В свою очередь газ, перешедший в пограничный слой, является носителем некоторого момента импульса исходной вихревой структуры. Логично предположить, что данный момент импульса является для системы потерянным благодаря действию сил вязкостного трения.
Полученные соотношения не позволяют получить в явном виде зависимости выходной частоты первичных вихревых преобразователей с прецессирующей струей. Тем не менее, возможно численное решение данных уравнений, позволяющее оценить влияние тех или иных факторов на интересующие процессы.
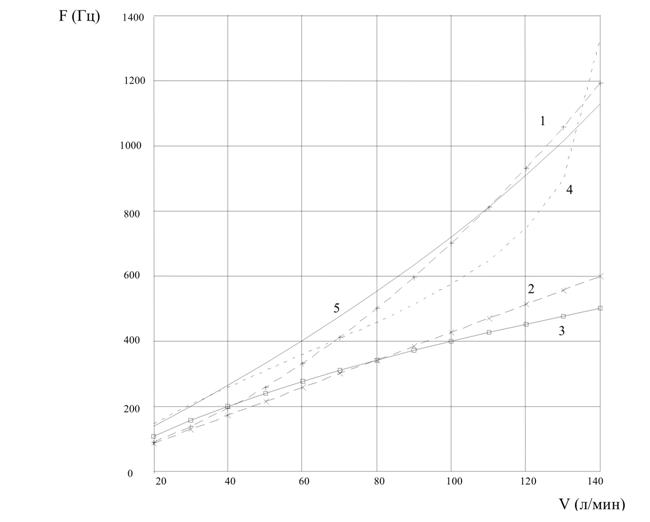
Рассчитанные с использованием приведенных выше соотношений зависимости расход/частота для системы, состоящей из вихреобразующей камеры высотой 8 мм с 8-ю каналами и формирующего патрубка диаметром 16 мм в сравнении с экспериментальными данными для подобной системы, представлены на рисунке 2.
Здесь:
· кривая 1 - аппроксимирующий экспериментальные данные полином 2-й степени.
· прямая 2 - случай несжимаемой среды (уравнение 16),
· кривая 3 - сжимаемая среда без учета образования пограничного слоя и потерь энергии на преодоление сил вязкостного трения,
· кривая 4 - сжимаемая среда с учетом образования пограничного слоя и без учета потерь энергии на преодоление сил вязкостного трения для расстояния 10.9 мм от начала ФП,
· кривая 5 - сжимаемая среда с учетом образования пограничного слоя и учетом потерь энергии на преодоление сил вязкостного трения для расстояния 34 мм от начала формирующего патрубка.
|
· |
|
Рисунок 2. Частотная зависимость, полученная экспериментальным путем для системы, состоящей из ВОК высотой 8мм и 8-ю подающими каналами с максимальной шириной и ФП, диаметром 16 мм (кривая 1) на расстоянии 34 мм от его начала в сравнении с рассчитанными по моделям: без учета сжимаемости, образования буферной области и потерь энергии (прямая 2), только с учетом сжимаемости (кривая 3), с учетом образования буферной области для сжимаемой среды без потерь вращательного момента импульса (кривая 4 - на расстоянии 1.09 см от начала ФП, на больших расстояниях решение отсутствует) и с учетом потерь энергии (кривая 5). |
Как видно из графиков, учет сжимаемости приводит к уменьшению частоты вращения вихревой структуры по сравнению с несжимаемой средой, что объясняется увеличением массы периферийной области с соответствующим увеличением момента инерции при увеличении расхода. В свою очередь, учет образования буферной области без потерь энергии приводит к потере решения системы уравнений для зон формирующего патрубка, отстоящих от его начала на расстояниях, превышающих некоторое критическое значение. Связанно это с тем фактом, что уменьшение массы вращающегося объема газа за счет образования буферной области приводит к уменьшению момента инерции вихревой структуры что требует, для выполнения закона сохранения импульса, роста частоты вращения вплоть до значений, превосходящих максимальное обрабатываемое машиной (стремиться к бесконечности). Расчетные зависимости в этом случае имеют характер, близкий к полученным для случая, не учитывающего образование буферного слоя, при низких расходах либо на малых расстояниях от начала формирующего патрубка, что соответствует незначительной интенсивности его образования.
Наиболее, по характеру кривой рабочей зависимости, экспериментальным данным соответствуют результаты, полученные в случае учета, как образования буферного слоя, так и потерь вращательного момента импульса. Кроме этого, решение данной системы может быть найдено для любых расстояний от начала ФП, что приводит к выводу о наибольшем соответствии этой модели реальной ситуации. Значение коэффициента А в уравнении 25, при котором достигается наилучшее приближение расчетных данных к экспериментальным, лежит в диапазоне от 1.4 до 2.4, что соответствует турбулентному движению газа в трубопроводе.
Список литературы:
1. Юдаев Б.Н. Техническая термодинамика. М.: Высшая школа, 1988. 497 с.
дипломов


Оставить комментарий