Статья опубликована в рамках: V Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 12 декабря 2011 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
ОСОБЕННОСТИ ДВИЖЕНИЯ ТОРОВЫХ ВНУТРИТРУБНЫХ ПРИВОДОВ В ХОДЕ ФОРМИРОВАНИЯ ЦЕМЕНТНОГО ПОКРЫТИЯ
Давыденко Ольга Васильевна
эксперт, ФГБОУ ВПО «Ставропольский государственный университет»,
г. Ставрополь
E-mail: labeta@mail.ru
Движение рукава в трубопроводе в ходе нанесения покрытия носит нагруженный характер, причем для каждого случая, в зависимости от характера совокупности сопротивлений, препятствующих выворачиванию рукава в трубопроводе, расчет минимального давления выворачивания рукава должен производиться индивидуально. В рамках настоящей работы определены выражения для расчета минимального давления выворачивания для двух вариантов исполнения устройства для нанесения покрытия.
Рассмотрим первый вариант исполнения установки: для нанесения смеси используется совокупность разомкнутой тороидальной оболочки (рукава) и поршня-заглушки (как показано на рисунке 1).

Рисунок 1 – Схема участка, восстанавливаемого с использованием совокупно рукава и поршня
Находящийся в полости между рукавом и поршнем цементно-песчаный раствор, используемый в качестве покрывающей смеси, представляет собой вязко-пластичную неньютоновскую жидкость [3]. Для начала движения необходимо создать определенную разность давлений, соответствующую равенству возникающего на стенке трубопровода касательного напряжения ![]() и начального напряжения сдвига жидкости
и начального напряжения сдвига жидкости ![]() . При этом вся масса жидкости движется как твердое тело с одинаковыми скоростями для всех частиц [1].
. При этом вся масса жидкости движется как твердое тело с одинаковыми скоростями для всех частиц [1].
Следует отметить, что используемый в качестве покрывающего состав на основе цемента является тиксотропным, ввиду чего ![]() зависит от времени. Однако для небольших промежутков времени между приготовлением смеси и началом восстановительных работ
зависит от времени. Однако для небольших промежутков времени между приготовлением смеси и началом восстановительных работ ![]() можно считать постоянным.
можно считать постоянным.
Принципиально, предельное напряжение сдвига является достаточно трудноопределимой величиной, точное экспериментальное определение которой требует специализированного лабораторного оборудования, неприменимого в построечных условиях. Однако, для исследуемого диапазона подвижностей цементно-песчаной смеси (6-9 см) справедливо следующее приближенное выражение для расчета ![]() через осадку стандартного конуса [2]:
через осадку стандартного конуса [2]:
|
|
(1) |
где ![]() - объемный вес смеси, кг/см3;
- объемный вес смеси, кг/см3; ![]() – объем конуса, см3;
– объем конуса, см3; ![]() - площадь нижнего основания конуса после осадки, см2;
- площадь нижнего основания конуса после осадки, см2; ![]() - ускорение свободного падения. При исследуемых величинах осадки стандартного конуса радиус верхнего основания конуса
- ускорение свободного падения. При исследуемых величинах осадки стандартного конуса радиус верхнего основания конуса ![]() допускается, для простоты расчета, полагать неизменным. В таком случае радиус нижнего основания и, соответственно, его площадь
допускается, для простоты расчета, полагать неизменным. В таком случае радиус нижнего основания и, соответственно, его площадь ![]() можно определить, исходя из условия постоянства объема смеси. Запишем его:
можно определить, исходя из условия постоянства объема смеси. Запишем его:
|
|
(2) |
где ![]() - объем нормального конуса, см3;
- объем нормального конуса, см3; ![]() – объем конуса после осадки, см3;
– объем конуса после осадки, см3; ![]() – высота нормального конуса, см;
– высота нормального конуса, см; ![]() – радиус верхнего основания нормального конуса, см;
– радиус верхнего основания нормального конуса, см; ![]() – радиус нижнего основания нормального конуса, см;
– радиус нижнего основания нормального конуса, см; ![]() - осадка конуса, см;
- осадка конуса, см; ![]() – радиус нижнего основания конуса после осадки, см.
– радиус нижнего основания конуса после осадки, см.
Проведя элементарные преобразования и подставив в выражение (3) известные и постоянные для используемого типа конуса величины, получим:
|
|
(4) |
Полученное приближенное выражение (4) позволяет, в совокупности с (3), осуществлять расчет предельного напряжения сдвига ![]() на основе простых, легко определяемых характеристик раствора: осадки стандартного конуса и объемного веса смеси.
на основе простых, легко определяемых характеристик раствора: осадки стандартного конуса и объемного веса смеси.
Запишем условие равновесия системы сил, действующих на рассматриваемый объем покрывающей смеси:
|
|
(5) |
где ![]() - площадь поперечного сечения рукава, м2. В проекции на ось S:
- площадь поперечного сечения рукава, м2. В проекции на ось S:
|
|
(6) |
Сила трения ![]() , возникающая у стенок трубы на боковой поверхности рассматриваемого объема, может быть представлена выражением:
, возникающая у стенок трубы на боковой поверхности рассматриваемого объема, может быть представлена выражением:
|
|
(7) |
где ![]() - длина пробки покрывающего состава в трубопроводе, м.
- длина пробки покрывающего состава в трубопроводе, м.
Сила трения покоя ![]() , преодоление которой необходимо для начала движения поршня-заглушки, равна:
, преодоление которой необходимо для начала движения поршня-заглушки, равна:
|
|
(8) |
где ![]() – коэффициент трения сцепления, а
– коэффициент трения сцепления, а ![]() – сила нормального давления, равная
– сила нормального давления, равная ![]() . Тогда:
. Тогда:
|
|
(9) |
откуда можно выразить критическое давление выворачивания:
|
|
(10) |
Таким образом, условие движения рассматриваемой совокупности рукава, покрывающей смеси и поршня-заглушки, в рамках принятых допущений, представляет собой критическое давление выворачивания рукава и зависит от физико-механических характеристик используемой покрывающей смеси, ее количества, конструктивных параметров рукава, поршня-заглушки и восстанавливаемого трубопровода.
Рассмотрим второй вариант исполнения установки: для нанесения смеси используется совокупность двух разомкнутых тороидальных оболочек (рукавов) (как показано на рисунке 2).
 Рисунок 2 – Схема участка, восстанавливаемого с использованием двух рукавов
Рисунок 2 – Схема участка, восстанавливаемого с использованием двух рукавов
Запишем условие равновесия системы сил, действующих на рассматриваемый объем покрывающей смеси:
|
|
(11) |
в проекции на ось S:
|
|
(12) |
Подставив выражение (7) для силы трения ![]() и проведя элементарные алгебраические преобразования, получим:
и проведя элементарные алгебраические преобразования, получим:
|
|
(13) |
В рассматриваемой системе критическое давление выворачивания управляемо и зависит, в том числе, от произвольно устанавливаемого давления в запирающем рукаве. Для начала выворачивания рукава при любом произвольно установленном запирающем давлении ![]() в трубопроводе необходимо создать разность давлений, определяемую в соответствии с (13). Возможность произвольного варьирования давления выворачивания, при этом, имеет большое практическое значение.
в трубопроводе необходимо создать разность давлений, определяемую в соответствии с (13). Возможность произвольного варьирования давления выворачивания, при этом, имеет большое практическое значение.
Скорость разворачивания рукава под действием давления выворачивания ![]() определяется в соответствии с выражением
определяется в соответствии с выражением
|
|
(14) |
Однако, если разворачивание покрывающего рукава происходит самопроизвольно, то запирающий рукав необходимо удалять из трубопровода принудительно. При этом, не учитывая потери длины пробки раствора в ходе движения ее по трубопроводу, положим, что скорость выведения запирающего рукава должна быть равна скорости, вычисленной по (14). Соответственно, для обеспечения возможности разворачивания покрывающего рукава в трубопроводе запирающий рукав должен сматываться с равной скоростью.
В результате настоящей работы получены выражения для минимального давления выворачивания покрывающего рукава в двух вариантах исполнения установки для нанесения покрытия. Показано, что в случае использования в качестве запирающего элемента второго рукава возможно произвольное регулирование давлений, поддерживаемых в полостях рукавов, что имеет большую практическую ценность.
Список литературы:
1.Рабинович Е.З. Гидравлика: учебное пособие / Е.З. Рабинович. - М.: Недра, 1980.
2.Черкасов Г.И. Введение в технологию бетона. – Иркутск: Восточно-Сибирское книжное издательство, 1974.
3.Neville A.M. Properties of concrete. – England, Essex: Prentice Hall, 2008.
дипломов


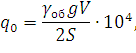
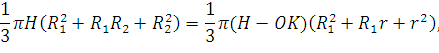
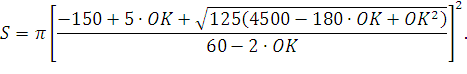

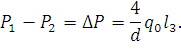
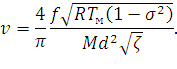
Оставить комментарий