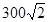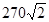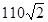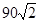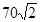ОСОБЕННОСТИ ФУРЬЕ – И ВЕЙВЛЕТ-СПЕКТРОВ

ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ РАБОТЫ

Коваленко Дмитрий Валерьевич

аспирант,

Омский государственный технический университет,

РФ, г. Омск

E-mail: Dmitrii_Kovalenko92@mail.ru

PARTICULARLY THE FOURIER AND WAVELET SPECTRUM

FOR NON-STATIONARY OPERATING MODE

Dmitriy Kovalenko

graduate, Omsk State Technical University,

Russia, Omsk

АННОТАЦИЯ

В статье рассмотрены графики тока, напряжения и спектра Фурье при различных режимах работы простейшей электрической системы, а также показан эффект «растекания спектра», который появляется при построении спектра Фурье для нестационарных сигналов. Рассмотрены пространственные вейвлет-спектры нестационарного режима при различных значениях масштаба.

ABSTRACT

The article describes the graphs of current, voltage and Fourier spectrum for different modes of operation of the simplest electrical system, and shows the effect of "spectrum leakage" that appears when you build a Fourier spectrum for non-stationary signals. Considered, the spatial wavelet spectra of non-stationary modes for different values of the scale.

Ключевые слова: вейвлет-преобразование; преобразование Фурье; стационарный режим; нестационарный режим; Фурье-спектр; вейвлет-спектр.

Keywords: wavelet transform; Fourier transform; stationary regime; non-stationary regime; Fourier spectrum; wavelet spectrum.

Существует два основных метода, позволяющих проводить спектральный анализ сигналов: преобразование Фурье и метод вейвлет-преобразования. Описанию этих методов посвящено достаточно большое количество работ [1–9]. В работах [2; 7] достаточно подробно рассматривается теория дискретного и непрерывного вейвлет-преобразования. Также, в этих работах выполнен краткий обзор практического применения этих методов. В настоящей статье внимание читателя обращено на Фурье-спектры гармоник простейшей электрической системы при различных режимах работы (стационарном и нестационарном) и на трехмерные вейвлет-спектры при различных значениях параметра масштаба.

На рисунке 1 приведена схема замещения простейшей электрической системы. Параметры элементов: R=22,5 Ом, L=38,2 мГн.

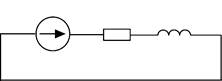
Рисунок 1. Схема замещения простейшей электрической системы

Вначале смоделируем стационарный режим работы. Это такой режим работы, при котором не происходит внезапных изменений («скачков») сигнала за рассматриваемый промежуток времени.

Зададим источник ЭДС периодическим несинусоидальным сигналом, имеющим постоянную составляющую, основную (первую), третью, пятую, седьмую и девятую гармоники (начальную фазу для упрощения расчета примем равной нулю).

,

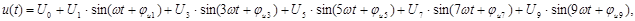
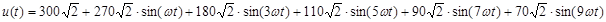где: 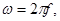 f – частота сети (50 Гц).

Индуктивные и полные сопротивления отдельных гармоник определяются по следующим формулам (Ом)[1]:

, .

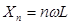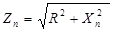Фазы токов отдельных гармоник (градус):

.

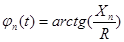Амплитудные значения токов отдельных гармоник определяются как (А):

.

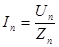Отсюда уравнение сигнала тока будет иметь следующий вид:

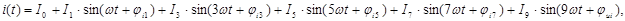Результаты расчетов приведены в таблице 1.

Таблица 1.

Результаты расчетов

Примечание к таблице: индуктивное сопротивление постоянной составляющей рассчитывается как индуктивное сопротивление постоянному току, т. е. при 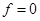 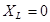и полное сопротивление равно активному

Графики напряжения, тока и Фурье-спектр приведены на рисунке 2.

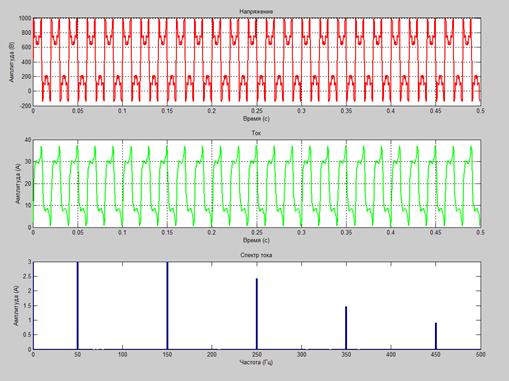
Рисунок 2. Графики напряжения, тока и Фурье-спектра при стационарном режиме работы

Далее смоделируем нестационарный режим работы. Нестационарный режим – это такой режим, при котором происходит внезапное изменение («скачок») сигнала за рассматриваемый промежуток времени.

Параметры системы рассчитываются по аналогии со стационарным режимом (поэтому и результаты вычислений будут подобными), однако графики режима будут несколько иные (рисунок 3).

Также на рисунках 4–6 показаны трехмерные графики вейвлет-спектров (графики вейвлет-спектров приведены для нестационарного режима за исключением вейвлет-спектра, приведенного на рисунок 7. – Это стационарный режим).

В работе [2] автор дает следующее определение вейвлет-спектра: «Вейвлет-спектр представляет собой поверхность в трехмерном пространстве. Вид поверхности определяет изменения во времени спектральных компонентов различного масштаба и называется частотно-временным спектром».

При построении трехмерных графиков вейвлет-спектров использовались: вейвлет Морле, непрерывное вейвлет-преобразование (CWT). Значения масштабирующего параметра в различных диапазонах: а=(1; 35) для спектра, изображенного на рисунке 4, а=(1; 25) для рисунка 5, а=(1; 5) для рисунка 6). При внимательном рассмотрении рисунка 6 нетрудно убедиться, что левая и правая части спектра (по оси времени) различны: в правой части заметны «штрихи», которые сообщают нам, что мы имеем дело с нестационарным режимом. Если бы мы строили вейвлет-спектр для стационарного режима, то он был бы ровным и не имел бы никаких «штрихов». Это хорошо иллюстрируется графиком вейвлет-спектра, приведенного на рисунке 7.

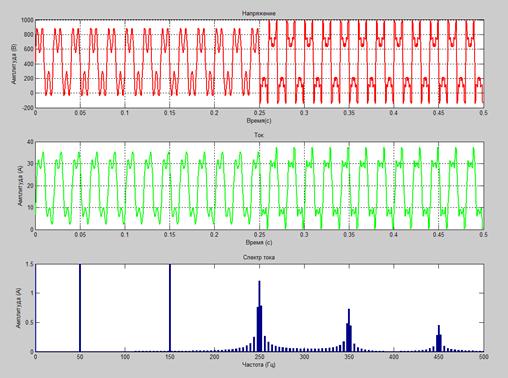
Рисунок 3. Графики напряжения, тока и Фурье-спектра при нестационарном режиме работы

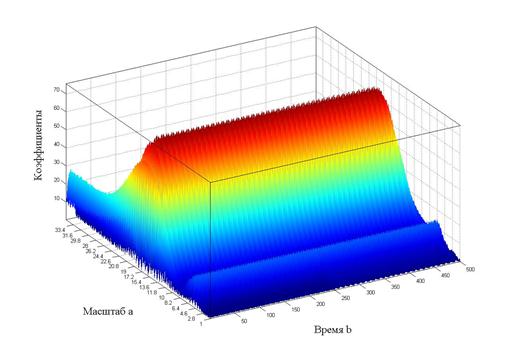
Рисунок 4. Вейвлет-спектр при коэффициенте масштаба а=35 (нестационарный режим)

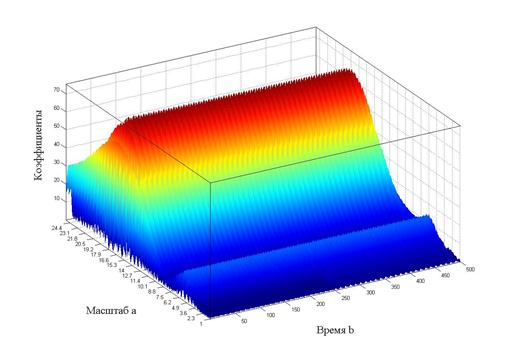
Рисунок 5. Вейвлет-спектр при коэффициенте масштаба а=25 (нестационарный режим)

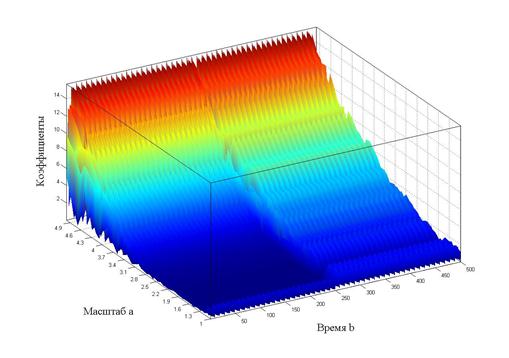
Рисунок 6. Вейвлет-спектр при коэффициенте масштаба а=5 (нестационарный режим)

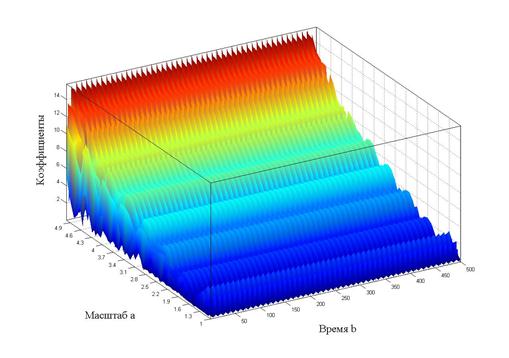
Рисунок 7. Вейвлет-спектр при коэффициенте масштаба а=5 (стационарный режим)

Рассматривая графики стационарного и нестационарного режимов (рисунки 2, 3), можно сделать следующие выводы:

1. Графики напряжения и тока в первом случае (рисунок 2) одинаковые на всем рассматриваемом промежутке времени (стационарный режим работы). Во втором случае (рисунок 3) форма графиков напряжения и тока резко изменяется (в момент t=0,25 с). Это связано с тем, что в этот момент времени в системе происходят резкие и серьезные изменения, что нашло отражение в графиках напряжения и тока (нестационарный режим работы).
2. Из графика Фурье-спектра видно, что в стационарном режиме Фурье-спектр четкий (видны только вертикальные линии – постоянная составляющая и гармоники – 50 (основная), 150 (третья), 250 (пятая), 350 (седьмая) и 450 (девятая), Гц – четные гармоники отсутствуют, так как рассматриваемая нами система не имеет выпрямителей или частотных преобразователей). В нестационарном режиме наблюдается эффект «растекания спектра» с появлением огромного количества ложных частот, которых не существует в реальности – появляется множество «штрихов» на графике (особенно сильно это проявляется в спектре пятой, седьмой и девятой гармониках, имеющих частоты 250, 350 и 450 Гц).

Анализируя графики вейвлет-спектров (рисунки 4–7), можно сделать следующие выводы.

1. Трехмерный вейвлет-спектр – это представление сигнала в трехмерном пространстве (именно поэтому он является поверхностью).
2. Изменение параметра масштаба позволяет рассмотреть, как общую картину спектра (при большом диапазоне изменения параметра а), так и локальные области спектра (при малом диапазоне изменения параметра а). Таким образом, мы получаем своеобразный «микроскоп», который позволяет «просматривать» как весь спектр, так и его отдельные области.
3. Вейвлет-спектр (при правильно выбранном масштабе) позволяет нам судить о характере режима (стационарный или нестационарный).

Заключение.

Преобразование Фурье основано на представлении сигнала в базисе функций синусов и косинусов, бесконечно повторяющихся (периодичных) во времени. Фурье-спектр при нестационарном режиме работы имеет множество ложных частот (проявляется эффект «растекания спектра»).

Вейвлет-преобразование основано на разложении сигнала базисными функциями, которые имеют временное ограничение. Поэтому при анализе нестационарных режимов оно имеет преимущество перед преобразованием Фурье.

Список литературы:

1.    Бессонов Л.А. Теоретические основы электротехники. Электрические цепи / Л.А. Бессонов. – Москва: «Высшая школа». – 1996. – 638 с.

2.    Вейвлет-анализ в примерах: учебное пособие / О.В. Нагорнов, В.Г. Никитаев, В.М. Простокишин и др. – Москва: НИЯУ МИФИ, 2010. – 120 с.

3.    Воробьев В.П. Теория и практика вейвлет-преобразования / В.П. Воробьев, В.Г. Грибунин. – Санкт-Петербург. – 1999. – 203 с.

4.    Давыдов А.В. Цифровая обработка сигналов: Тематические лекции / Екатеринбург: УГГУ, ИГиГ, кафедра геоинформатики. – 2007 – 2010.

5.    Осипов Д.С. Применение вейвлет-преобразования для расчета мощности в системах электроснабжения при нестационарных режимах работы / Д.С. Осипов, Д.В. Коваленко, Л.А. Файфер // Инновации в науке: Сборник статей по материалам LI Международной научно-практической конференции. – Новосибирск: изд. СибАК. – 2015. – № 11 (48).

6.    Осипов Ю.М. Частотный и временной анализ стационарных и переходных характеристик линейных электрических цепей: учебное пособие по курсам электротехники и ТОЭ, в 2-х ч. / Ю.М. Осипов; Санкт-Петербургский государственный институт точной механики и оптики (Технический университет). – Санкт-Петербург. – 2002. – 129 с. – 2 ч.

7.    Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB / Н.К. Смоленцев. – Москва: ДМК Пресс. – 2005. – 304 с.

8.    Яковлев А.Н. Введение в вейвлет-преобразования: учебное пособие / А.Н. Яковлев. – Новосибирск: Изд-во НГТУ, 2003. – 104 с.

9.    Paul S. Addison. The Illustrated Wavelet Transform Handbook: Introductory Theory and Application in Science, Engineering, Medicine and Finance / Paul S. Addison. – Institute of Physics Publishing Bristol and Philadelphia. – 2002. – 362 p.