АНАЛИЗ  ОБЕСПЕЧЕННОСТИ  НОРМАТИВНЫХ  И  РАСЧЕТНЫХ  НАГРУЗОК  НА  ОСНОВАНИИ  СОВРЕМЕННЫХ  НОРМ

Сухина  Ксения  Николаевна

старший  преподаватель  кафедры  «Строительные  конструкции,  основания  и  надежность  сооружений»,

Волгоградский  государственный  архитектурно-строительный  университет,

РФ,  г.  Волгоград

E-mail:  ya.elektronka2011@yandex.ru

ANALYSIS  OF  THE  SECURITY  OF  REGULATORY  AND  SETTLEMENT  LOADS  ON  THE  BASIS  OF  MODERN  STANDARDS

Kseniya  Suhina

senior  Lecturer  department  “Building  construction,  grounds  and  reliability  of  structures”,

University  of  architecture  and  civil  engineering,  Russia,  Volgograd

АННОТАЦИЯ

В  статье  представлен  алгоритм  вычисления  всех  необходимых  статистических  характеристик  снеговой  нагрузки  по  их  расчетным  значениям,  приведенным  в  нормативных  документах,  а  также  представлены  результаты  исследований  фактической  снеговой  нагрузки  и  ее  обеспеченности  в  г.  Волжском  Волгоградской  области.

ABSTRACT

The  paper  presents  an  algorithm  for  calculating  the  necessary  statistical  characteristics  of  the  snow  load  on  their  calculated  values  given  in  the  regulations,  as  well  as  the  results  of  studies  of  actual  snow  loads  and  its  security  in  the  Volzhsky  city  of  Volgograd  region.

Ключевые  слова:  обеспеченность;  статистический  момент;  индекс  надежности;  метеостанции;  коэффициент  вариации.

Keywords:  security;  statistical  moment;  reliability  index;  weather  stations;  the  coefficient  of  variation.

Применение  вероятностных  методов  для  расчета  зданий  и  сооружений  на  действие  различных  нагрузок  является  достаточно  сложным  процессом,  т.  к.  требует  наличия  обширных  статистических  данных  [1;  2;  4].  Вместе  с  тем,  задачи  такого  рода  могут  быть  решены  на  основании  нормативных  данных  и  исследованиях,  регламентированных  современными  нормами.

Рассмотрим  снеговые  нагрузки.  Для  этого,  на  первом  этапе,  проведем  анализ  реализаций  ежегодных  максимумов  снеговой  нагрузки  за  последние  43  года,  полученных  метеостанциях,  расположенных  в  разных  снеговых  районах  (табл.  1).

Таблица  1.

Статистические  характеристики  снеговых  нагрузок

На  основании  полученных  данных,  представленных  в  таблице  1  найдем  индекс  надежности  для  расчетного  значения  снеговой  нагрузки:

                                       (1)

Выразив  переменные  в  правой  части  формулы  (1)  через  параметры  закона  Гумбеля  получаем:

·     расчетная  нагрузка 

  ,                              (2)

·     математическое  ожидание

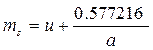  ,                 (3)

·     стандарт 

  .                           (4)

Откуда

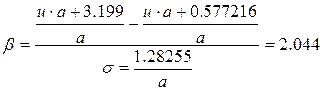    (5)

То  есть,  интервал    соответствует  2.044  стандартам:

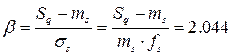  ,                    (6)

Отсюда  следует,  что 

.                       (7)

С  учетом  того,  что  коэффициент  вариации  ежегодных  максимумов  снеговой  нагрузки  для  всех  районов  приблизительно  одинаков  f_s=0,4,  выражение  (7)  можно  записать  в  виде:

.                                        (8)

По  известным  расчетным  значениям  снеговой  нагрузки,  приведенным  в  [3],  можно  определить  все  требуемые  статистические  характеристики  случайной  величины  ее  годичных  максимумов,  а  также  параметры  закона  распределения  Гумбеля  для  всех  снеговых  районов. 

В  качестве  примера  найдем  вероятность  превышения  фактической  снеговой  нагрузкой  расчетное  значение  в  городе  Волжском  Волгоградской  области,  относящегося  ко  II-му  снеговому  району.  По  табл  10.1  [3]  получаем,  что  расчетное  значение  S_q  составляет  120  кг/м².

Тогда  используя  формулу  (8)  получим,  что

·     математическое  ожидание  годичных  максимумов:  кг/м²;

·     коэффициент  вариации:  ;

·     стандарт:    кг/м²;

·     параметры  закона  Гумбеля:  ;  .

Плотность  распределения  максимумов:

          (9)

Функция  распределения  максимумов:

  .        (10)

Т.  к.  среднее  значение  периода  повторяемости  снеговой  нагрузки  составляет  25  лет,  соответствующее  25,  найдем  значение  S_q. 

Значение  функции  распределения:

  ,  (11)

то  есть  обеспеченность  снеговой  нагрузки  S_q  составляет  0,96.  Тогда  из  уравнения 

    (12)

выразим  S_q:

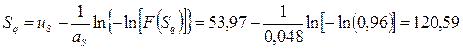  кг/м²  (13)

Таким  образом,  вес  снегового  покрова  на  поверхности  земли,  превышаемый  в  среднем  1  раз  в  25  лет,  вычисленный  г.  Волжского,  составляет  S_q=120,59  кг/м².  На  основании  карты  снеговых  районов  находим,  что  Волжский  относится  ко  II  снеговому  району,  для  которого,  согласно  табл.1,  S_q=120  кг/м².

Зная  фактические  и  расчетные  значения  снеговой  нагрузки  в  рассматриваемом  районе  можно  легко  найти  вероятность  превышения  значения  наибольшей  нагрузки  за  любой  временной  период. 

Вероятность  того,  что  фактическая  нагрузка  не  превысит  расчетную  на  протяжении  25  лет  находиться  по  формуле:

    (14)

Тогда  вероятность  превышения  будет  равна:

    (15)

Т.  е.  вероятность  того,  что  фактическая  снеговая  нагрузка  превысит  расчетную  за  период  25  лет  составляет  65  %.

На  рисунке  1  представлен  график  изменения  вероятности  превышения  снеговой  нагрузкой  заданный  уровень  120  кг/м²  во  времени.

Рисунок  1.  График  превышения  снеговой  нагрузкой  заданный  уровень  120  кг/м²  во  времени

Список  литературы:

1.            Райзер  В.Д.  Теория  надежности  сооружений.  Научное  издание.  –  М.:  Издательство  АСВ,  2010.  –  С.  384.

2.            Ржаницын  А.Р.  Теория  расчета  строительных  конструкций  на  надежность.  –  М.:  Стройиздат,  1978.  –  С.  285.

3.            Свод  правил:  СП  20.13330.2011  «Нагрузки  и  воздействия»  [Текст]:  нормативно-технический  материал.  М.:  Минрегион  России,  2011.  –  С.  98.

4.            Шпете  Г.  Надежность  несущих  строительных  конструкций.  М.:  Стройиздат,  1994.  –  С.  288  –  перевод  изд.:  Gerhard  Spaethe.  –  Die  Sicherheit  tragende  Bankonstruktionen.  –  ISBN.5-274-01208-6.