Статья опубликована в рамках: LI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 30 ноября 2015 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ПРИМЕНЕНИЕ ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЯ ДЛЯ РАСЧЕТА МОЩНОСТИ В СИСТЕМАХ ЭЛЕКТРОСНАБЖЕНИЯ ПРИ НЕСТАЦИОНАРНЫХ РЕЖИМАХ РАБОТЫ
Осипов Дмитрий Сергеевич
канд. техн. наук, доцент Омского государственного технического университета,
РФ, г. Омск
E-mail:
Коваленко Дмитрий Валерьевич
аспирант, Омский государственный технический университет,
РФ, г. Омск
E-mail: Dmitrii_Kovalenko92@mail.ru
Файфер Лилия Андреевна
магистрант группы ЭЭм-143, Омский государственный технический университет,
РФ, г. Омск
" target="_blank">
APPLICATION OF WAVELET TRANSFORM TO CALCULATE THE POWER IN POWER SYSTEMS UNDER NON-STATIONARY OPERATING MODES
Dmitriy Osipov
candidate of Technical Sciences, assistant professor Omsk State Technical University, Russia, Omsk
Dmitriy Kovalenko
graduate, Omsk State Technical University, Russia, Omsk
Liliya Fajfer
undergraduate of EEm-143 group,
Omsk State Technical University, Russia, Omsk
АННОТАЦИЯ
В статье рассмотрены краткие теоретические сведения вейвлет преобразования, Фурье преобразования, а также основные направления применения вейвлет преобразования в электроэнергетике.
В настоящей работе предложен способ определения активной, реактивной и полной мощностей на основе коэффициентов дискретного вейвлет преобразования. Проведено сравнение полученных результатов имитационного моделирования с известными способами. Также кратко были упомянуты особенности применения этих методов (преобразования Фурье и вейвлет преобразования).
ABSTRACT
The article describes a brief theory of wavelet transformation, Fourier transformation and basic directions of applications of wavelet transform in power.
In this paper we propose a method for determining active, reactive and apparent power based on the coefficients of the discrete wavelet transform. A comparison of the results of simulation with known methods. Also briefly mentioned was the particular application of these methods (Fourier transform and wavelet transform).
Ключевые слова: вейвлет; вейвлет преобразование; преобразование Фурье; расчет мощностей; стационарный и нестационарный режимы. Keywords: wavelet; wavelet transform; Fourier transform; capacity calculations; stationary and nonstationary regimes.
О происхождении термина «вейвлет» в работе [4] автор отмечает: «Слово wavelet – английское. Оно происходит от французского “ondelette” и переводится как «короткая (или маленькая) волна». В различных зарубежных статьях, переведенных на русский язык, можно встретить и другие варианты перевода (например, «всплеск», «всплесковая функция», «маловолновая функция», «волночка»).
Вейвлет-преобразование произвольного одномерного сигнала – это представление сигнала обобщенным рядом, либо интегралом Фурье по системе базисных функций
![]() ,
,
полученных из исходного вейвлета ψ(t), который обладает определенными свойствами «за счет операций сдвига во времени b и изменения временного масштаба a. Множитель 1/a обеспечивает независимость нормы этих функций от масштабирующего числа a». При заданном значении параметров a и b функция ψab(t) является вейвлетом. И одновременно производной материнского вейвлета ψ(t).
Идеи теории вейвлет-анализа возникли с появлением большого количества рядов экспериментальных данных, обработка которых методом Фурье-преобразования показала ограниченность последнего для поиска закономерностей в них.
Один из первых, кто понял ограниченность применение фурье-анализа, был А. Хаар, опубликовавший систему базисных функций, которые обладали основными свойствами вейвлетов. Эта работа появилась в 1910 году, а сам термин «вейвлет» появился почти через 70 лет. Система функций, которую ввел Хаар обладала свойствами, присущими для вейвлетов, а именно: локальной областью определения (ограниченными носителями), ортогональностью и единичной нормой, нулевым средним и самоподобием (автомодельностью).
Приведем популярные (также называемые иногда классическими) вейвлеты [1].
«Haar-вейвлет:

Рисунок 1. Вейвлет Хаара
Mhat-вейвлет ("Мексиканская шляпа"):

Рисунок 2. Вейвлет «Мексиканская шляпа»
Вейвлет Морле (образует комплексный базис, изображена действительная часть)»:
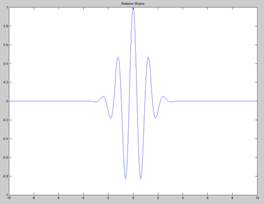
Рисунок 3. Вейвлет Морле
Рассмотрим в качестве примера вейвлет функцию и модуль спектральной плотности этой функции (рис. 4, 5).
«Малые значения параметра а соответствуют мелкому масштабу вейвлет-функции ψab(t) или высоким частотам (ω ~ 1/a ), большие значения a – крупному масштабу вейвлет-функции ψab(t)» [4]. Иначе говоря, мы растягиваем исходный вейвлет ψ(t) и сжимаем его спектр.
Если рассматривать частотную область, то спектры вейвлетов напоминают, так называемые, всплески или волночки. (Именно из-за этого обстоятельства встречаются и такие варианты перевода слова wavelet на русский язык, как «волночка»). Они (всплески и волночки) имеют пик на частоте ω0 и полосу Δω (полосовой фильтр); при этом величины ω0 и Δω снижаются при увеличении параметра a.
Из вышесказанного следует, что вейвлеты локализованы не только во временной, но и в частотной областях.
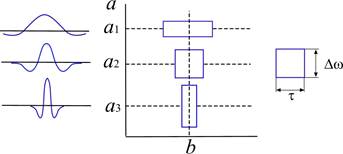
Рисунок 4. Масштабирование вейвлет-функции
Вейвлет-преобразование может быть дискретным и непрерывным.
Непрерывное вейвлет преобразование. Непрерывное вейвлет преобразование функции s(t) Î L2(R) – это функция двух переменных:
![]() ,
, ![]() ,
,
в которой вейвлеты
дипломов


Оставить комментарий