МАТЕМАТИЧЕСКИЕ  МОДЕЛИ  ДЛЯ  КАЧЕСТВЕННОЙ  ОЦЕНКИ  ПРОИЗВОДИТЕЛЬНОСТИ  СЕМАФОРОВ  МНОГОПРОЦЕССОРНЫХ  ВЫЧИСЛИТЕЛЬНЫХ  СИСТЕМ

Мартышкин  Алексей  Иванович

канд.  техн.  наук,  доцент  кафедры  Вычислительных  машин  и  систем

Пензенского  государственного  технологического  университета, 
РФ,  г.  Пенза

E-mail:  Alexey314@yandex.ru

Карасева  Елена  Александровна

магистрант  кафедры  Вычислительных  машин  и  систем

Пензенского  государственного  технологического  университета, 
РФ,  г.  Пенза

E-mail: 

MATHEMATICAL  MODEL  FOR  QUALITATIVELY  ASSESS  THE  PERFORMANCE  OF  SEMAPHORES  OF  MULTIPROCESSOR  COMPUTING  SYSTEMS

Alexey  Martyshkin

candidate  of  Science,  assistant  professor  Department  of  Computational  Systems  and  Machines 
of  Penza  State  Technological  University, 
Russia,  Penza

Elena  Karaseva

master  student  Department  of  Computational  Systems  and  Machines 
of  Penza  State  Technological  University, 
Russia,  Penza

Работа  выполнена  при  финансовой  поддержке  стипендии  Президента  РФ  молодым  ученым  и  аспирантам  на  2015—2017  гг.  (СП-828.2015.5)

АННОТАЦИЯ

В  статье  рассмотрены  математические  модели  управления  доступом  множества  процессов,  выполняющихся  на  множестве  процессоров,  к  общему  ресурсу  на  основе  стратегий  спин-блокировки  и  блокировки  в  ядре.

ABSTRACT

The  article  considers  mathematical  models  of  access  control  of  multiple  processes  running  on  multiple  processors  to  a  shared  resource  based  on  strategies  for  spin  locks  and  blocking  in  the  kernel.

Ключевые  слова:  многопроцессорная  вычислительная  система;  параллельные  процессы;  семафор;  общий  ресурс;  критическая  секция;  латентность;  блокировки  в  ядре;  спин-блокировка.

Keywords:  multiprocessor  computer  systems;  parallel  processes;  semaphore;  shared  resource;  critical  section;  latency;  locking  in  the  kernel;  spin  lock.

Семафоры  применяют  для  координации  доступа  к  одиночному  общему  ресурсу  (ОР),  или  фиксированному  множеству  ОР  несколькими  параллельными  процессами  [2].  Проблема  производительности  семафоров  заключается  в  том,  что  во  взаимодействующих  процессах  возникают  одновременные  требования  доступа  к  ОР,  которые  приводят  к  конфликтным  ситуациям,  а  они  в  свою  очередь  приводят  к  потерям  общей  производительности  операционной  системы  (ОС).  Наиболее  характерно  это  проявляется  в  многопроцессорных  вычислительных  системах  (МПВС),  когда  взаимодействующие  процессы  реализуются  в  независимых  процессорах  (ЦП),  функционирующих  в  мультипрограммном  режиме.  Если  ресурс  требуется  слишком  большому  числу  ЦП,  то  они  ставятся  в  очередь.  При  этом  запросы  обслуживаются  по  принципу  FIFO  или  по  приоритетам.

Различают  методы  управления  доступом  к  ОР  в  пространстве  пользователя  и  в  пространстве  ядра  ОС.  Механизм  критических  секций  (КС)  заключается  в  том,  что  если  процесс,  пытающийся  получить  доступ  к  ОР,  находит  его  занятым,  то  он  должен  ждать  освобождения  ОР.  Это  ожидание  может  быть  организовано  следующими  способами:  1)  находясь  в  активном  ожидании,  т.е.  процесс  занимает  некоторый  ЦП,  непрерывно  пытаясь  получить  доступ  к  своей  КС;  2)  процесс  должен,  освободив  ЦП,  перейти  в  состояние  блокировки  до  тех  пор,  пока  не  будут  одновременно  свободны  КС  и  ЦП.  Первая  из  приведенных  выше  стратегий  реализуется  в  пространстве  пользователя  и  носит  название  «спин-блокировки»,  вторая  —  реализуется  непосредственно  ОС  и  называется  блокировкой  в  ядре.  Недостатком  спин-блокировки  является  тот  факт,  что  ЦП,  выполняющий  соответствующий  процесс,  пребывает  в  непроизводительном  простое  в  течение  всего  времени  ожидания  доступа  к  ОР.  Блокировка  процесса  в  ядре  приводит  к  переключению  текущего  процесса  и,  следовательно,  к  возможной  перезагрузке  кэш-памяти  ЦП,  что  требует  существенных  временных  затрат  и  увеличивает  вероятность  кэш-промаха.  Перезагрузка  кэш  возникает  в  связи  с  тем,  что  после  выхода  процесса  из  состояния  блокировки  он  с  высокой  вероятностью  будет  назначен  на  другой  ЦП.  В  кэш  этого  ЦП  естественно  не  будет  блоков,  в  которых  бы  содержались  данные  рассматриваемого  процесса  [2].

Основными  характеристиками  производительности  методов  доступа  к  ОР  приняты:  латентность  семафора  —  время,  требуемое  процессу  на  захват  и  освобождение  семафора;  латентность  доступа,  которую  определим  как  время  ожидания  доступа  к  КР  в  условиях  конкуренции  множества  параллельных  процессов.  Как  латентность  семафора,  так  и  латентность  доступа  вносят  накладные  расходы  на  вычислительный  процесс,  реализующий  процедуру  доступа  к  ОР,  которые  приводят  к  большим  потерям  производительности  выполняющихся  программ.

К  рассмотрению  принята  МПВС,  ОС  которой  реализует  метод  планирования  с  разделением  пространства,  когда  каждый  процессорный  узел  (ПУ)  имеет  собственную  очередь  готовых  процессов  (ОГП).  Общая  схема  выполнения  процессов  с  учетом  обращения  к  ОР  представлена  на  рис.  1. 

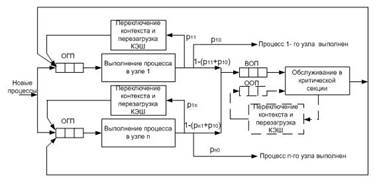
Рисунок  1.  Общая  схема  выполнения  процессов  с  учетом  обращения  к  общему  ресурсу

Новые  процессы  помещаются  в  ОГП.  Каждый  процесс  из  ОГП  получает  квант  процессорного  времени,  по  истечении  которого  происходит  прерывание  текущего  процесса  и  переключение  контекста,  после  чего  текущий  процесс  с  вероятностью  p₁₁,…,  p_1n  помещается  в  конец  очереди,  а  из  очереди  выбирается  на  обслуживание  следующий  процесс.  Выполненные  процессы  с  вероятностями  p₁₀,…,p_n0  покидают  ПУ.  Обращение  процессов  к  ОР,  который  обслуживается  в  КС,  происходит  с  вероятностями  [1-  (p₁₁+  p₁₀)],…,  [1-  (p_1n+  p_n0)].  Первоначально  все  запросы  на  доступ  в  КС  помещаются  во  входную  очередь  процессов  (ВОП).  На  рис.  1  показаны  два  варианта  доступа  процессов  к  ОР:  1)  с  применением  спин-блокировки,  когда  переключение  контекста  не  происходит.  Если  КС  занята,  то  процесс  сканирует  семафор  до  тех  пор,  пока  тот  не  освободится;  2)  с  применением  блокировки  в  ядре,  когда  при  занятости  семафора  происходит  немедленное  переключение  контекста  с  целью  перемещения  процесса  из  ОГП  в  очередь  ожидающих  процессов  (ООП)  и  обратно  после  освобождения  КС  [1].

Модель  управления  одиночным  общим  ресурсом. 

Стохастические  модели  для  оценки  латентности  описанных  выше  методов  доступа  к  ОР  представлены  на  рис.  2.  ПУ  выступают  в  качестве  источника  заявок,  формирующих  запросы  в  КС  каждого  процесса.  Будем  считать,  что  процессы,  выполняемые  в  ЦП,  являются  идентичными,  а  сами  ЦП  одинаковыми.  В  этом  случае  МПВС  буде  генерировать  поток  запросов  на  доступ  к  семафору  с  интенсивностью  ,  где    —  интенсивности  запросов  к  ОР  i-го  ЦП.

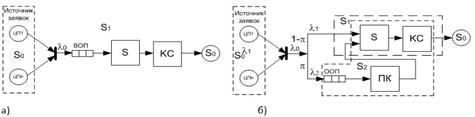
Рисунок  2.  Схемы  математических  моделей  МПВС  с  одним  ОР  на  основе  семафора  со  спин-блокировкой  (а)  и  с  блокировкой  в  ядре  (б)

На  рис.  2:  ЦП_i  —  процессорные  узлы;  S  —  семафор;  КС  —  критическая  секция;  ПК  —  переключение  контекста;  ВОП  —  очередь  входных  процессов;  ООП  —  очередь  ожидающих  (блокированных)  процессов.

Математические  модели  представлены  в  виде  открытых  систем  массового  обслуживания  (СМО).  Первая  модель  (рис.  2а)  представлена  одноканальной  СМО,  которой  в  качестве  обслуживающих  ресурсов  выступают  время,  требуемое  процессу  на  захват  и  освобождение  семафора    и  время  работы  в  КС  .  СМО  S₀  выполняет  функцию  внешнего  источника  заявок  и  поглотителя  обслуженных  заявок  [1]. 

Вторая  модель  —  стохастическая  сеть  (рис.  2б),  состоящая  из  двух  одноканальных  СМО  S₁  и  S₂.  Здесь  поток  запросов    разделятся  на  два  подпотока    и  .  Заявки  из  потока    поступают  на  вход  СМО  S₁,  моделирующую  процедуру  входа  и  обслуживания  в  КС  в  условиях  отсутствия  конкуренции.  Интенсивность  таких  запросов  составляет  .  Входная  очередь  в  СМО  S₁  не  образуется  в  связи  с  тем,  что  процесс,  получивший  отказ  в  обслуживании  в  КС,  немедленно  перемещается  в  ООП.  В  то  же  время  процесс,  поступивший  в  отсутствие  конкуренции,  немедленно  получает  обслуживание.  Заявки  из  потока    поступают  на  вход  СМО  S₂,  моделирующую  обслуживание  запросов  в  условиях  конкуренции.  Интенсивность  таких  запросов  составляет  .  Здесь  в  модель  обслуживания  вносится  дополнительное  время,  затрачиваемые  на  переключение  контекста  ,  которое  тоже  создает  накладные  расходы,  являющиеся  непроизводительными. 

C  учетом  ранее  отмеченного  считаем,  что  время  между  подачей  запроса  на  доступ  к  КС  и  входом  в  КС  составляет  латентность  доступа  ,  а  время,  затраченное  на  захват  семафора  —  латентность  семафора  .  Обозначим  через    время  доступа  к  ОР  по  стратегии  спин-блокировки,  а  через    –  время  доступа  по  стратегии  блокировки  в  ядре  соответственно.  С  учетом  указанного  выше  латентность  доступа  по  стратегии  спин-блокировки  определится  как  время  ожидания  в  очереди  для  одноканальной  СМО  и  времени,  требуемого  на  захват/освобождение  семафора  :

,                                                     (1)

а  латентность  доступа  по  стратегии  блокировки  в  ядре: 

  .                                    (2)

Результаты  моделирования  представлены  на  графике  (рис.  3),  где  верхняя  кривая  соответствует  латентности  доступа  по  стратегии  блокировки  в  ядре,  а  нижняя  —  латентности  по  стратегии  спин-блокировки.

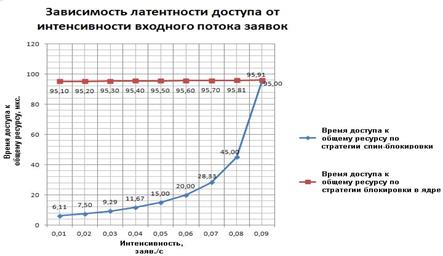
Рисунок  3.  График  результатов  моделирования

Очевидно,  что  при  небольшой  интенсивности  потоков  запросов  стратегия  спин-блокировки  является  оптимальной.  В  условиях  высокой  нагрузки  стратегия  блокировки  в  ядре  становится  более  предпочтительной.

Список  литературы:

1. Бикташев  Р.А.  Модели  оценки  производительности  средств  синхронизации  параллельных  процессов.  //  Вопросы  радиоэлектроники,  серия  ЭВТ,  —  2010,  —  вып.  5,  —  c.  21—29.
2. Таненбаум  Э.,  Бос  Х.  Современные  операционные  системы.  —  СПб.:  Питер,  2015.  —  1120  с.