АППАРАТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В ИССЛЕДОВАНИЯХ МЕТАЛЛУРГИЧЕСКОГО ПРОИЗВОДСТВА

Швалёва Анна Викторовна

канд. пед.наук, доцент НФ НИТУ «МИСиС», г. Новотроицк

E-mail: 

В черной металлургии имеется много процессов, в которых действует большое количество факторов. Таковы, например, исследо­вания процессов выплавки стали, свойств сложных железоугле­родистых сплавов, дефектов при прокатке и т. д. Параметры металлур­гического производства носят массовый случайный характер. Теория случайных процессов — раздел математической науки, изучающий закономерности случайных явлений в динамике их развития. 

Статистические методы обработки данных стали привычным и широко распространенным аппаратом для инженеров металлургичес­кого производства для оценки результатов механических испытаний, хими­ческого состава стали и температурно-деформационных парамет­ров. Это послужило причиной роста требований к качеству статистической обработки экспериментальных данных, соответствен­но к компетентности инженера в области прикладной статистики. Однако, как показывает практика, выпускник технического вуза оказы­вается не всегда готов к выполнению исследовательской деятельности, особенно если речь идет об использовании достаточно большого объема математических средств. Зачастую, это является следствием формальности изложения дисциплины, и студенты, имея даже хоро­ший запас знаний, не всегда могут его использовать в профессиональ­ной деятельности. Мотивация изучения студентами этого раздела (не очень простого, надо отметить,  в восприятии) может быть обеспечена осознанием ими значимости статистики для будущей профессии. С этой целью содержание дисциплины целесообразно наполнять профес­сионально-ориентированными задачами, исследовательскими заданиями.

Ориентация на практическое использование знаний предполагает постановку задач с учетом будущей профессиональной деятельности студента, подбор конкретного материала и выбор формы организации работы [2, c. 121].

Новотроицкий филиал «МИСиС» готовит специалистов по заказу металлургического комбината ОАО «Урал Сталь», это позволяет тесно взаимодействовать преподавателям и студентам с предприятием. Преподавателями кафедры математики и естествознания Новотроиц­кого филиала «МИСиС» была организована работа с центральной лабораторией комбината, c целью выявить аппарат математической статистики, используемый в исследованиях металлургического производства.    

Существуют несколько основных понятий, необходимых для эффективного использования методов современной статистики. Одним из таковых является выборочная совокупность — понятие, лежащее в основе всех статистических методов, и представляющее собой часть объектов из генеральной совокупности, отобранных для изучения, с тем, чтобы сделать заключение о всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна быть представительной. Значительные объемы производства металлопроката, стабилизация технологического процесса производст­ва позволили сформировать представительную выборочную совокуп­ность и разработать математические модели для расчета уровня меха­нических свойств в зависимости от углеродного эквивалента, химичес­кого состава стали и технологических параметров прокатки.

Чтобы обеспечить однородность выборочной совокупности необходимо учитывать следующие факторы:

• нормативную документацию;
• марку стали;
• период времени;
• агрегат выплавки;
• состояние поставки.

Следующим шагом является составление вариационного ряда — в возрастающем порядке располагаются значения признака и указываются относительно каждого варианта частота. Этот ряд харак­теризует изменение (варьирование) значений признака. Можно проде­монстрировать изображение вариационного ряда графически (полигон распределения, гистограмма). 

В качестве одного из важнейших параметров статистики является средняя величина (арифметическая, геометрическая, гармоническая, квадратичная, кубическая). Чаще используют арифметическую среднюю [1, с. 200], вычисляемую по формуле:

Средние величины, характеризуя частотный ряд одним числом, не учитывают разброса признака. Для измерения колебания признака используют вариационный размах, дисперсию и среднее квадра­тическое отклонение. Вариационный размах R есть разность между экстремальными значениями частотного ряда: R=x_max–x_min. Вариа­ционный размах — величина неустойчивая, зависящая от случайных обстоятельств. Дисперсия— средняя арифметическая из квадратов отклонений вариантов от их средней арифметической [1, с. 206]: 

По сравнению со значениями случайной величины, дисперсия измеряется в квадратных единицах. Для того, чтобы иметь меру рас­сеяния, сопоставимую со значениями средней величины, используют среднее квадратическое отклонение случайной величины:

Часто для характеристики колеблемости признака используют относительные показатели: коэффициент вариации,  представляющий собой отношение среднего квадратического отклонения к средней арифметической:

.

Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах.

Следующим важным звеном в исследовательском аппарате инженера является владение законами распределения. Наблюдая многочисленные ряды распределения, исследователи стремятся по­строить теоретическое распределение, исходя из данных эмпири­ческого распределения.  Теоретическим законом многих рядов, встре­чаемых на практике, является нормальное распределение, которое зависит от средней арифметической и квадратического отклонения. Это объясняется теоремой А. М. Ляпунова: если случайная величина представляет собой сумму большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно, то величина имеет распределение, близкое к нормаль­ному [1, с. 135]. Умение выявить нормальное распределение в некото­ром эмпирическом ряде является важным условием для практических расчетов. Зная, что фактическое распределение является нормальным, можно определить оптимальные размеры резервов, оптимальное содержание элементов химического состава в металле. Для того, чтобы определить, является ли данное распределение нормальным, исполь­зуют специально подобранные случайные величины, называемые критериями согласия. В технических исследованиях наиболее часто употребляемыми являются критерии Пирсона, Стьюдента, Романовс­кого, Колмогорова и др. Для оценки близости эмпирического распре­деления к теоретическому используется критерий Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности. С этой целью сравнивают эмпирические (наблюдаемые)  и теорети­ческие (вычисленные в предположении нормального распределения) частоты. Случайная величина имеет вид:

.

Чем меньше различаются эмпирические и теоретические частоты, тем меньше значение критерия, что свидетельствует о близости эмпирического и теоретического распределений. По таблице значений критических точек распределения хи-квадрат, заданному уровню значимости и числу степеней свободы находят критическую точку и сравнивают наблюдаемым значением.  

При изучении распределений, отличных от нормального, возни­кает необходимость количественно оценить это различие [3, с. 158]. Оценку можно произвести с помощью характеристик: асимметрии (A_s — свидетельствует о симметрии кривой распределения) и эксцесса (E_k — оценка «крутости» кривой, то есть большего лил меньшего подъема кривой распределения относительно нормальной кривой):

,

где: ;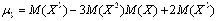

.

Для нормального распределения  эти величины нулевые. Если асимметрия и эксцесс — небольшие величины, это свидетельствует о близости распределения к нормальному.

Уже только этот описанный аппарат математической статистики (а это лишь очень немногая часть) позволяет оценить статистические параметры и построить частотные распределения массовой доли хими­ческих элементов в различных видах стали и механических свойств (характеристик растяжения: предела текучести, временного сопротив­ления, относительного удлинения; вязких свойств — ударной силы). В качестве примера в таблицах 1 и 2 приведены статистические парамет­ры и частотные распределения массовой доли химических элементов C и Si в стали одной марки, выплавленной в электродуговых печах. 

Таблица 1

Статистические параметры

Таблица 2

Частотные распределения массовой доли химических элементов

После определения необходимого математического аппарата, преподаватель формулирует учебно-профессиональную исследова­тельскую задачу — ситуацию, требующую от студентов мыслитель­ных и практических действий, направленных не только на усвоение ими профессиональных знаний и умений, но и на овладение исследо­вательскими умениями, на приобретение опыта исследовательской деятельности [4, с. 6]. В качестве таковой может быть оценка стабиль­ности технологического процесса (постоянство механических свойств марки стали при одном технологическом процессе) или зависимость механических свойств стали от химического состава.

Статистические данные по механическим свойствам предназначены:

• для анализа показателей качества выпускаемой продукции;
• дальнейшего совершенствования технологии производства;
• улучшения качественных показателей металлопродукции;
• для подбора оптимальной марки-аналога на основе идентично производимой и сопоставимой продукции по механическим свойствам.

Список литературы:

1. Гмурман В. Е. Теория вероятностей и математическая статистика. Учеб. Пособие для вузов. — изд. 7-е, стер. — М.: Высш. шк., 2001. — 479 с.
2. Земцова В. И. Управление учебно-профессиональной деятельностью сту­дентов на основе функционально-деятельностного подхода: Монография. — М.: Компания Спутник+, 2008. — 208 с.
3. Калинина В. Н., Панкин В. Ф. Математическая статистика: Учеб. Для сту. Сред. Спец. Учеб. Заведений. — 3-е изд., испр. — М.: Высш. шк., 2001. — 336 с.
4. Методика решения учебно-профессиональных исследовательских задач при изучении естественнонаучных дисциплин (на примере курса общей физики): методические рекомендации для студентов технических специальностей / сост. И. А. Ткачева. — Орск: Издательство ОГТИ, 2009. — 63 с.