Статья опубликована в рамках: VIII Международной научно-практической конференции «Экономика и современный менеджмент: теория и практика» (Россия, г. Новосибирск, 21 декабря 2011 г.)
Наука: Экономика
Секция: Экономические аспекты регионального развития
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРОГНОЗИРОВАНИЕ УРОВНЯ ИНВЕСТИЦИОННОЙ ПРИВЛЕКАТЕЛЬНОСТИ РЕГИОНОВ
Алексеева Оксана Анатольевна
канд. экон. наук, доцент кафедры экономики и управления СевКавГТУ,
г. Ставрополь
E-mail: tokmolotok@yandex.ru
Формирование эффективной региональной социально-экономической политики невозможно без проведения широкого круга аналитических и методологических работ, одно из направлений которых – региональное прогнозирование. В условиях России региональный аспект прогнозирования играет особую роль, поскольку без учета специфики развития регионов не может быть реализована ни одна долгосрочная общегосударственная программа, невозможно проведение никаких социальных и экономических реформ. Кроме того, только прогнозы территориального развития позволяют определить вероятность возникновения кризисных ситуаций в различных субъектах Федерации, а также оценить саму возможность реализации основных направлений государственной экономической политики в различных сферах и на разных уровнях.
Предвидение основных направлений социально-экономического развития регионов предполагает использование специальных вычислительных и логических приемов, позволяющих определить параметры функционирования отдельных элементов производительных сил в их взаимосвязи и взаимозависимости. Систематизированное научно обоснованное прогнозирование развития социально-экономических процессов осуществляется с первой половины 50-х годов XXвека, хотя некоторые методики прогнозирования были известны и ранее.
В развитии методологии прогнозирования социально-экономических процессов большую роль сыграли научные разработки отечественных и зарубежных ученых А.Г. Аганбегяна, И.В. Бестужева-Лады, Л. Клейна, В. Гольдберга и др. В работах этих ученых рассматривается значение, сущность и функции прогнозирования, его роль и место в системе планирования, исследуются вопросы методологии и организации экономического прогнозирования, показываются особенности научного прогнозирования. Развитие работ, освещающих вопросы прогнозирования, осуществляются по таким основным направлениям: углубление теоретических и прикладных разработок нескольких групп методик, отвечающих требованиям разных объектов и разных видов работ по прогнозированию; разработка и реализация на практике специальных способов и процедур использования различных методических приемов в ходе конкретного прогнозного исследования; поиск путей и способов алгоритмизации методик прогнозирования и реализация их с использованием ЭВМ [1].
Под методами прогнозирования следует понимать совокупность приемов и способов мышления, позволяющих на основе анализа ретроспективных данных, экзогенных (внешних) и эндогенных (внутренних) связей объекта прогнозирования, а также их измерений в рамках рассматриваемого явления или процесса вывести суждения определенной достоверности относительно его (объекта) будущего развития [2].
По оценкам отечественных и зарубежных ученых, в настоящее время насчитывается свыше 20 методов прогнозирования, однако число базовых значительно меньше. Многие из них относятся скорее к отдельным приемам и процедурам, учитывающим нюансы объекта прогнозирования. Другие представляют собой набор отдельных приемов, отличающихся от базовых или друг от друга количеством частных приемов и последовательностью их применения.
Процедура построения прогноза инвестиционной привлекательности регионов подразумевает предварительное решение ряда задач:
1.подобрать эконометрическую модель зависимости инвестиционной привлекательности регионов от предикторов, ее формирующих (потенциал и ограничения);
2.выявить силу влияния каждого предиктора на результирующий показатель инвестиционной привлекательности региона;
3.определить приоритетные факторы, отвечающие за потенциал и ограничения, формирующие инвестиционную привлекательность региона и выявить их взаимосвязь при формировании итогового показателя.
Для решения первой задачи в ходе построения прогноза инвестиционной привлекательности региона необходимо определить вид и характер зависимости существующих тенденций в динамике исследуемого показателя. Для этого производится подбор теоретического уравнения регрессии для региона на основе использования производственных функций.
Первоначально строится линейная модель взаимосвязи инвестиционной привлекательности региона и факторов, его формирующих (потенциал и ограничения).
Линейное двухфакторное уравнение регрессии имеет вид:
 ,
,
где а, b1и b2– параметры уравнения регрессии; x1и x2– экзогенные переменные; y – эндогенная (результирующая) переменная.
В проводимом исследовании результатом взаимодействия таких факторов, как потенциал (х1) и ограничения (х2) развития региона, является показатель инвестиционной привлекательности (у). То есть факторы являются ресурсами, а инвестиционная привлекательность региона – результатом.
Для решения поставленной задачи построения прогноза инвестиционной привлекательности региона рассматривается возможность применения и других (нелинейных) видов производственных функций:
· степенная: 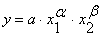 ;
;
· показательная:  ;
;
· обратная: 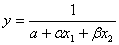 ;
;
· полулогарифмическая: ;
;
· гиперболическая: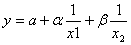 ;
;
· экспоненциальная: 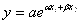
где α и β– параметры уравнения регрессии.
При этом для нелинейных функций проводится их линеаризация. Нелинейные регрессии по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов.
Адаптируя используемые модели к особенностям проводимого исследования определим, что параметры α и β характеризуют зависимость (эластичность) инвестиционной привлекательности региона (у) от объема и динамики элементов его формирующих (х1 и х2), причем α характеризует прирост y, приходящийся на единицу приростаx1 (при x2 = const), а β – прирост y, приходящийся на единицу прироста x2(приx1= const). Параметр aотражает влияние не идентифицированных, т. е. не учтенных в модели факторов и меняющихся условий инвестиционной привлекательности.
Апробация представленных моделей прогноза инвестиционной привлекательности регионов проводилась на регионах Юга России (табл. 1).
Таблица 1.
Результаты построения двухфакторной регрессионной модели инвестиционной привлекательности регионов Юга России
|
Наименование региона |
Уравнение регрессии |
Параметры оценки уравнения регрессии |
||
|
Коэффициент корреляции |
F-критерий |
Ошибка аппроксимации |
||
|
ВО |
y= 2,280 + 0,062 ∙ x1 - 0,142 ∙ x2 |
0,9999 |
18078,2 |
0,227 |
|
РО |
y= 2,786 + 0,063 ∙ x1- 0,175 ∙ x2 |
0,9996 |
4621,1 |
0,605 |
|
КК |
|
0,999 |
7703,3 |
0,07 |
|
ЧР |
y= 0,269 + 0,076 ∙ x1- 0,020 ∙ x2 |
0,9954 |
385,4 |
3,267 |
|
РСОА |
y= 1,831 + 0,104 ∙ x1- 0,189 ∙ x2 |
0,9995 |
3950,3 |
0,586 |
|
КЧР |
y= 1,125 + 0,112 ∙ x1- 0,126 ∙ x2 |
0,9999 |
14305,2 |
0,278 |
|
РК |
y= 1,219 + 0,104 ∙ x1- 0,125 ∙ x2 |
0,9958 |
415,8 |
2,516 |
|
КБР |
y= 1,388 + 0,129 ∙ x1- 0,177 ∙ x2 |
0,9989 |
1707,6 |
1,047 |
|
РИ |
y= 0,769 + 0,099 ∙ x1- 0,077 ∙ x2 |
0,9992 |
2112,1 |
0,951 |
|
РД |
y= 2,107 + 0,124 ∙ x1- 0,260 ∙ x2 |
0,9997 |
6377,8 |
0,542 |
|
АО |
y= 1,074 + 0,106 ∙ x1- 0,123 ∙ x2 |
0,9991 |
1955,4 |
1,040 |
|
СК |
|
0,999 |
2290,00 |
0,27 |
|
РА |
y= 1,145 + 0,099 ∙ x1- 0,113 ∙ x2 |
0,9998 |
10596,2 |
0,251 |
Полученный результат позволяет констатировать тот факт, что по одиннадцати из исследуемых регионов линейная модель наиболее точно и качественно определяет взаимосвязь потенциала, ограничений и инвестиционной привлекательности регионов. Взаимосвязь указанных факторов и функции по Краснодарскому краю описываются полулогарифмической моделью, а по Ставропольскому краю – гиперболической моделью.
Полученные регрессионные модели обеспечивают достаточно высокую корреляционную связь и приемлемый уровень ошибки аппроксимации в регрессионном уравнении, что позволяет сделать вывод о возможности их использования в целях прогноза.
Решение второй поставленной задачи позволило сделать вывод, что с ростом потенциала региона уровень инвестиционной привлекательности увеличивается. При этом при росте ограничений, напротив, происходит снижение итогового показателя. По одиннадцати из исследуемых регионов коэффициенты регрессии при х2 больше, чем соответствующий показатель при х1, следовательно ограничения в развитии оказывают большее влияние на формирование уровня инвестиционной привлекательности регионов Юга России. Только по двум регионам наблюдается противоположная взаимосвязь (Чеченская Республика и Республика Ингушетия).
Для решения третьей поставленной задачи построения прогнозной модели инвестиционной привлекательности регионов определяются частные коэффициенты эластичности и β-коэффициент (табл. 2).
Таблица 2.
Результаты расчета критериев, характеризующих влияние факторов, формирующих инвестиционную привлекательность регионов Юга России
|
Наименование региона |
коэффициент эластичности |
β-коэффициент |
||
|
х1 |
х2 |
х1 |
х2 |
|
|
ВО |
0,885 |
0,957 |
0,425 |
0,974 |
|
РО |
0,922 |
1,017 |
0,264 |
0,734 |
|
КК |
0,978 |
0,989 |
0,554 |
1,629 |
|
ЧР |
1,030 |
0,509 |
0,775 |
0,204 |
|
РСОА |
0,957 |
1,030 |
0,566 |
1,028 |
|
КЧР |
1,029 |
1,007 |
0,852 |
0,959 |
|
РК |
0,931 |
1,089 |
0,552 |
0,664 |
|
КБР |
1,041 |
0,995 |
1,083 |
1,486 |
|
РИ |
0,969 |
0,998 |
0,109 |
0,933 |
|
РД |
1,040 |
0,998 |
0,665 |
1,395 |
|
АО |
1,250 |
0,916 |
0,440 |
0,510 |
|
СК |
1,111 |
0,965 |
0,445 |
0,788 |
|
РА |
0,740 |
1,009 |
0,740 |
0,845 |
В результате получено, что при росте уровня потенциала на 1 единицу, инвестиционная привлекательность увеличится максимально на 1,250 единицы по Астраханской области, а минимально – на 0,740 по Республике Адыгея. По ограничениям имеем обратную связь, то есть при увеличении данного фактора на 1 единицу, показатель инвестиционной привлекательности региона снизится максимально по Республике Калмыкия на 1,089 единицы, минимально – на 0,509 единицы по Чеченской Республике.
β-коэффициент с математической точки зрения показывает, на какую часть величины среднеквадратического отклонения меняется среднее значение переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значениях независимых переменных. Максимум данного показателя имеется у Кабардино-Балкарской Республике по потенциалу и Краснодарскому краю – по ограничениям инвестиционной привлекательности регионов. Минимальные значения имеются по Ростовской области и Чеченской Республике соответственно.
Построение непосредственно прогноза инвестиционной привлекательности региона должно сопровождаться прогнозом предикторов, формирующих итоговый показатель. При этом в ходе проведенной оценки инвестиционной привлекательности регионов Юга России выявлено, что достигнутые в последние годы уровни потенциала и ограничений не могут меняться критически быстро. Поэтому для прогноза предикторов используется метод экспоненциального сглаживания, позволяющий придавать наибольшую значимость более поздним наблюдениям.
Результаты построения прогноза предикторов х1 и х2 представлены в таблице 3.
Таблица 3.
Результаты прогноза факторов, формирующих инвестиционную привлекательность регионов Юга России
|
Наименование региона |
Потенциал |
Ограничения |
||
|
Уравнение тренда |
Прогноз на 2012 год |
Уравнение тренда |
Прогноз на 2012 год |
|
|
ВО |
Y=0,1648∙t+29,697 |
31,84 |
Y=0,0405∙t+13,998 |
14,52 |
|
РО |
Y=-0,1178∙t+36,607 |
35,08 |
Y=0,0340∙t+15,341 |
15,78 |
|
КК |
Y=0,0529∙t+42,649 |
43,34 |
Y=0,0807∙t+14,970 |
16,02 |
|
ЧР |
Y=0,323∙t+4,879 |
9,08 |
Y=-0,28101∙t+17,158 |
13,51 |
|
РСОА |
Y=-0,2355∙t+16,775 |
13,71 |
Y=0,1262∙t+8,717 |
10,36 |
|
КЧР |
Y=-0,1084∙t+10,946 |
9,54 |
Y=-0,009∙t+9,632 |
9,51 |
|
РК |
Y=-0,308∙t+11,154 |
7,53 |
Y=0,147∙t+8,047 |
9,96 |
|
КБР |
Y=-0,286∙t+12,755 |
9,04 |
Y=-0,1349∙t+8,643 |
6,89 |
|
РИ |
Y=-0,1494∙t+8,709 |
6,77 |
Y=-0,064∙t+10,392 |
9,55 |
|
РД |
Y=0,0105∙t+17,216 |
19,17 |
Y=0,0414∙t+8,587 |
9,12 |
|
АО |
Y=-0,084∙t+18,807 |
17,71 |
Y=0,2143∙t+10,555 |
13,34 |
|
СК |
Y=-0,194∙t+25,613 |
23,09 |
Y=-0,0611∙t+13,346 |
12,56 |
|
РА |
Y=-0,2562∙t+13,638 |
10,31 |
Y=0,0166∙t+10,213 |
10,43 |
Построение прогноза инвестиционной привлекательности регионов осуществляется двух вариантах:
· точечный прогноз, получаемый с помощью подстановки в итоговое уравнение регрессии прогнозные значения предикторов х1 и х2;
· интервальный прогноз, в основе построения которого заложен расчет доверительного интервала, позволяющего учитывать случайные колебания:
· нижний интервал: 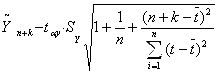 ,
,
· верхний интервал: 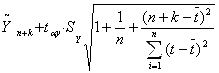 ,
,
где  – точечный прогноз;
– точечный прогноз; 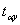 – t-критерий Стьюдента с доверительной вероятностью (1-α) и (n-1) степенями свободы;
– t-критерий Стьюдента с доверительной вероятностью (1-α) и (n-1) степенями свободы; 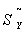 – стандартная ошибка прогнозируемого показателя; n– длительность предпрогнозного периода; k– период упреждения;t– момент наблюдения.
– стандартная ошибка прогнозируемого показателя; n– длительность предпрогнозного периода; k– период упреждения;t– момент наблюдения.
Стандартная ошибка прогнозируемого показателя определяется по формуле:
 ,
,
где m– число параметров модели.
Результаты расчета точечного и интервальных прогнозов представлены в таблице 4, по которой можно сказать, что с вероятностью 95% можно утверждать, что при сохранении сложившихся закономерностей инвестиционной привлекательности регионов прогнозируемые на 2012 год значения по избранным моделям попадут в промежуток, образованный нижней и верхней границей доверительного интервала.
Таблица 4.
Прогноз инвестиционной привлекательности регионов Юга России 2012 г.
|
Наименование региона |
Точечный прогноз |
Интервальный прогноз |
|
|
нижняя граница |
верхняя граница |
||
|
ВО |
2,192 |
2,155 |
2,230 |
|
РО |
2,235 |
2,142 |
2,326 |
|
КК |
2,702 |
2,629 |
2,776 |
|
ЧР |
0,689 |
0,585 |
0,792 |
|
РСОА |
1,299 |
1,227 |
1,370 |
|
КЧР |
1,099 |
1,075 |
1,122 |
|
РК |
0,757 |
0,588 |
0,927 |
|
КБР |
1,335 |
1,245 |
1,424 |
|
РИ |
0,704 |
0,664 |
0,743 |
|
РД |
2,113 |
2,045 |
2,180 |
|
АО |
1,310 |
1,213 |
1,408 |
|
СК |
1,831 |
1,759 |
1,904 |
|
РА |
0,987 |
0,957 |
1,017 |
Таким образом, мы можем отметить повышение инвестиционной привлекательности шести регионов Юга России (Волгоградской области, Краснодарского края, Чеченской Республики, Карачаево-Черкесской Республики, Ставропольского края и Республики Адыгея) в 2012 году.
В семи из исследуемых регионов Юга России в прогнозном периоде наблюдается ежегодная тенденция к снижению инвестиционной привлекательности, что связано в основном с негативными тенденциями их потенциала и ограничений в развитии.
Список литературы:
1.Горелов С. Математические методы в прогнозировании. М.: Прогресс, 1993. – 257 с.
2.Цыгичко В. Основы прогнозирования систем. М.: Финансы и статистика, 1986. – 768 с.
дипломов


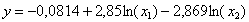
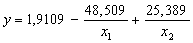
Оставить комментарий