ПОСТРОЕНИЕ СЕЗОННОЙ МОДЕЛИ ДЕЯТЕЛЬНОСТИ ЛИЗИНГОВОЙ КОМПАНИИ С ИСПОЛЬЗОВАНИЕМ ФИКТИВНЫХ РЕГРЕССОРОВ

Трифонова Елена Михайловна

ст. преподаватель, филиал КФУ, г. Набережные Челны

E-mail: telmi1@mail.ru

Сезонные модели считаются эффективным механизмом, способным повысить точность прогнозирования. Введение фиктивных регрессоров позволяет получить большое число наблюдений, что выступает важным фактором процесса прогнозирования, кроме того, с введением фиктивных переменных сезонные модели приобретают преимущества статистического подхода к моделированию, опираю­щегося на понятие вероятности.

Построение множественной регрессии начинается с введения фиктивных регрессоров (таблица 1).

Таблица 1.

Определение фиктивных регрессоров

Рассматривая модель множественной регрессии, будем опираться на модель, приведенную [1], нопериодичностью12 месяцев.

y_i'=b₁+s₁Ф_i⁽¹⁾+ s₂Ф_i⁽²⁾+ s₃Ф_i⁽³⁾+ s₄Ф_i⁽⁴⁾+ s₅Ф_i⁽⁵⁾+ s₆Ф_i⁽⁶⁾+ s₇Ф_i⁽⁷⁾++s₈Ф_i⁽⁸⁾+ s₉Ф_i⁽⁹⁾+ s₁₀Ф_i⁽¹⁰⁾+ s₁₁Ф_i⁽¹¹⁾+ s₁₂Ф_i⁽¹²⁾+e'_i,                    (1)

где y_i'=ln Y'_i, e'_i=lne_i.

Для нахождения коэффициентов регрессии приведенной модели, построим рабочую таблицу 2, содержащую значения фиктивных регрессоров от Ф⁽¹⁾ до Ф⁽¹¹⁾.

Таблица 2.

Определение значений фиктивных регрессоров

С помощью данной таблицы и опций MSExcel«Сервис→Анализ данных→Регрессия» получены следующие значения сезонного индекса и его 95% доверительные интервалы (в таблице 4 приведен отчет MSExcelдля модели s12).

Таблица 3.

Значения коэффициентов и соответствующих 95% доверительных интервалов для сезонной модели с фиктивными регрессорами (s12=0)

Сезонный индекс Sj определен по формуле [1, 220]:

Sj=exp(b₁+s_j),                                                 (2)

где    j=1,2,3…11

Таблица 4.

Расчет сезонных компонент

Для определения S₁₂используется формула:

S₁₂=exp(b₁)                                                      (3)

Для определения доверительного интервала S₁используется модель множественной регрессии y_i’ по всем фиктивным регрессорам, за исключением Ф_i⁽¹⁾:

y_i'=b₁^*+s₂^*Ф_i⁽²⁾+s₃^*Ф_i⁽³⁾+s₄^*Ф_i⁽⁴⁾+s₅^*Ф_i⁽⁵⁾+s₆^*Ф_i⁽⁶⁾+s₇^*Ф_i⁽⁷⁾+s₈^*Ф_i⁽⁸⁾++s₉^*Ф_i⁽⁹⁾+ s₁₀^*Ф_i⁽¹⁰⁾ + s₁₁^*Ф_i⁽¹¹⁾ + s₁₂^*Ф_i⁽¹²⁾ + e'^*_I                                                                  (4)

Таблица 5.

Значение коэффициентов по фиктивным регрессорам (Фi (1) исключен)

Из представленного отчета мы видим, что b₁^*= –0,5021091 имеет 95% доверительный интервал:

–2,70515<b₁^*<1,70093

Соответственно  получено значение коэффициента сезонности S₁:

S₁ = exp(b₁^*) = exp(–0,50211) =0,605252771

Значение полученного коэффициента соответствует значению, полученному при расчете модели в таблице 4.

Таблица 6.

Доверительный интервал для S₁

Чтобы получить доверительный интервал для оставшихся сезонных компонент, необходимо построить модель множественной линейной регрессии, последовательно исключая каждый из сезонных компонент, т. е. приняв фиктивный регрессор Фi=0. Алгоритм включения фиктивных регрессоров в модель линейной регрессии оформим в таблице 7.

Таблица 7.

Фиктивные регрессоры, образующие модель множественной регрессии

Таким образом, с помощью MSExcelполучены 12 отчетов, обработанные отчеты позволяют определить 95% доверительные интервалы для каждого сезонного индекса, при этом данные значения сезонных факторов не совпадают со значениями сезонных факторов, вычисленных методом скользящего среднего.

Таблица 8.

Коэффициенты сезонности и соответствующие им 95% доверительные интервалы

Полученные результаты представлены на рис.1.

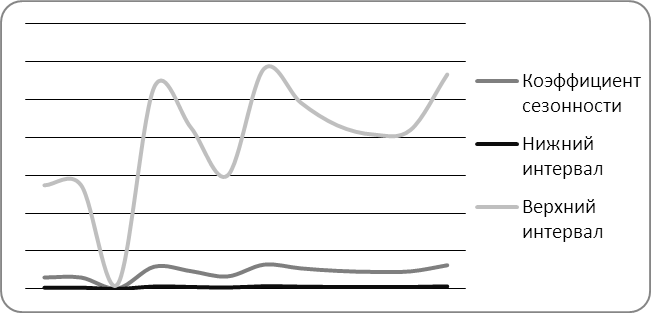
Рисунок 1. Сезонный индекс и соответствующие 95% доверительные интервалы

Таким образом, нами получены не только сезонные индексы, но еще и соответствующие им доверительные интервалы.

Далее с помощью expostпрогнозирования было проведено тестирование моделей с сезонным индексом полученных методом скользящего среднего и с использованием фиктивных регрессоров. Как при применении фиктивных регрессоров, так и в методе скользящей средней, использовавшихся при вычислении сезонных индексов, ошибка прогноза выходит за границы 95% рекурсивных интервалов прогноза. Но при использовании фиктивных регрессоров превышены только верхние значения границы,  а в методе скользящей средней —ошибки expostпрогнозов выходят как за верхние, так и за нижние границы интервалов. Обе модели плохо реагируют на выбросы. Величина ошибок в подавляющем большинстве превышает 10% от исходных данных временного ряда Y.

Список литературы:

1.        Слуцкин Л. Н. Курс МВА по прогнозированию в бизнесе / Л. Н. Слуцкин. —М. : Альпина Бизнес Букс, 2006. —277 с.