Статья опубликована в рамках: II Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 16 апреля 2012 г.)
Наука: Технические науки
Секция: Радиотехника, Электроника
Скачать книгу(-и): Часть I, Часть II, Часть III, Часть IV, Часть V
дипломов
Исследование ВЗАИМОСВЯЗИ ТЕПЛОВОГО РЕЖИМА РАБОТЫ ВЫСОКОЧАСТОТНЫХ ВАКУМНЫХ ВЫКЛЮЧАТЕЛЕЙ С РАЗМЕРАМИ ТОКОПРОВОДЯЩИХ ЭЛЕМЕНТОВ И КОНТАКТНЫМ НАЖАТИЕМ
Кожевникова Вероника Дмитриевна
студентка 2 курса, ФПЭИС, ПГТА, г. Пенза
E-mail: veronikakojev@mail.ru
Мешкова Оксана Александровна
студентка 2 курса, ФПЭИС, ПГТА, г. Пенза
Е-mail: po4ta1994@mail.ru
Бочкарев Владимир Семенович
научный руководитель, д-р. техн. наук., проф. каф. «Электроника и электротехника» ПГТА, г. Пенза
Ермолаев Николай Александрович
научный руководитель, канд. техн. наук., доцент. каф. «Информационные технологии и системы» ПГТА, г. Пенза
Тепловой режим работы высокочастотных вакуумных выключателей, переключателей и реле (высокочастотные вакуумные приборы коммутации - ВВПК) при пропускании тока высокой частоты зависит от омического сопротивления цепи их замкнутых контактов на высокой частоте, которое определяется геометрическими размерами токопроводников и контактным нажатием. Поэтому обеспечение нормального теплового режима ВВПК, являющегося гарантией надежной и долговечной их работы при эксплуатации, требовало установления взаимосвязи допустимого тока высокой частоты с геометрическими размерами их токопроводников и контактным нажатием. Для этого необходимо знать температуру в зоне контактирования, на поверхности токопроводящих элементов внутренней арматуры и внешней поверхности выводов (оболочки) при установившемся тепловом режиме.
Для нахождения температур нагрева элементов контактной зоны в вакууме составим уравнения теплового баланса [1] и объединим их условиями сопряжения [3]
 (1)
(1)
где t – время > 0; а12=λ1/с1m1 и а22=λ2/с2m2 – коэффициенты температуропроводности; λ1 и λ2, m1 и m2, c1 и с2 – коэффициенты теплопроводности, удельной массы и удельной теплоемкости материалов контактной группы; g1=If12ρ1/4π2λ2 и g2=If22ρ2/4π2λ2 – коэффициенты, характеризующие удельную мощность локальных источников тепла.
Для рассматриваемой системы уравнений в вакууме справедливы начальные и граничные условия идеального теплового контакта [2]:
![]() и
и ![]() . (2)
. (2)
В совокупности (1 и 2) приводятся к следующим уравнениям:
![]() и
и ![]() . (3)
. (3)
Решение (3) найдено с помощью интегрального преобразования Лапласа в следующем виде:
![]() (4)
(4)
где  ;
; 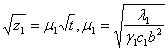 ;
;  ;
;  , где
, где ![]() .
.
Из (4) при ![]() (установившийся тепловой режим), получено следующее соотношение для расчета установившейся температуры контактной зоны Ту.кз. при пропускании тока высокой частоты:
(установившийся тепловой режим), получено следующее соотношение для расчета установившейся температуры контактной зоны Ту.кз. при пропускании тока высокой частоты:
![]() (5)
(5)
Поскольку температура окружающей среды То может отличаться от нуля, а нагрев контактной зоны дополнительно происходит за счет выделяемого тепла в токопроводниках Ту.пр, то общая (максимальная) температура контактной зоны Тм.кз. определяется выражением:
![]() . (6)
. (6)
При этом изотерма максимальной температуры в контактной зоне, при прохождении через нее тока высокой частоты, будет расположена по окружности радиусом а0, ибо плотность тока высокой частоты и потери максимальны на поверхности цилиндра, эквивалентного контактному переходу с радиусом а0.
Зависимость температуры нагрева в любой точке токопроводников от выделяемой в зоне контактирования мощности потерь может быть рассчитана по следующему известному выражению [1–3]:
 (7)
(7)
где х – текущая координата по направлению вдоль токопроводника или параллельно зоне контактирования.
В случае, когда температура окружающей среды не равна нулю, выражение (7) принимает вид:
 . (8)
. (8)
При одновременном учете температуры нагрева токопроводников пропускаемым через них током высокой частоты выражение (7) преобразуется к виду:
 (9)
(9)
Выделяемое при пропускании тока высокой частоты тепло dQ1 в единице длины токопроводника dx за время dt определяется выражением:
![]() , (10)
, (10)
где If – A (действ. знач.), Rf – Ом.
На повышение температуры токопроводника на dT расходуется тепло, определяемое известным соотношением [1]:
![]() , (11)
, (11)
где с – удельная теплоемкость единицы веса материала токопроводника,
Вт с/град.; Sп – поперечное его сечение, см2; m – удельный вес материала токопроводника, г/см3.
В вакууме отсутствует теплоотдача за счет конвекции, поэтому отвод тепла идет за счет излучения (Киз) с боковой поверхности Sб (см2) и теплопроводности (Кт) вдоль токопроводника:
![]() , (12)
, (12)
где Т и То – температура токопроводника и окружающей среды, °С;Ко=Киз+Кт – общий коэффициент теплоотдачи, равный для круглого токопроводника (8–13)·10-4 Вт/см2 ·°С и для прямоугольного – (6–9)·10 - 4 Вт/см2 ·°С .
С учетом (10–12), уравнение теплового баланса запишется в виде:
![]() , (13)
, (13)
которое после преобразования и разделения по переменным преобразуется к следующему виду:
![]() , (14)
, (14)
а с учетом температурной зависимости сопротивления токопроводника, уравнение (14) принимает вид:
![]() , (15)
, (15)
где Ro(f) – активное сопротивление токопроводника на высокой частоте при температуре 0 ºС.
После интегрирования (15) по переменной t от нуля до t, по переменной Т от Тн (температура наружной поверхности вывода) до Т, получаем:
 , (16)
, (16)
где τ = сmSп/KoSб-If12R0(f)α - постоянная времени нагрева токопроводника до установившейся температуры в секундах. При t, стремящемся к бесконечности, Т=Ту.пр, т.е. равна установившейся температуре токопроводника, а поэтому из (16) имеем:
 , (17)
, (17)
где ![]()
![]() – температурный коэффициент сопротивления.
– температурный коэффициент сопротивления.
В начальный момент пропускания тока высокой частоты температура наружной поверхности вывода равна температуре окружающей среды, т.е. Тн=То. Учитывая это, после подстановки (17) в (16) имеем:
![]() . (18)
. (18)
Выражение (18) позволяет найти температуру токопроводника, с неизменным по длине сечением, в любой момент времени пропускания тока высокой частоты.
Поскольку в ВВПК токопроводники имеют переменное сечение, необходимо их температуру рассчитывать с учетом повышенного нагрева локального участка с меньшим сечением. Для определения изменения температуры нагрева токопроводника по длине в этом случае составим тепловой баланс для его элемента длиной dx с сечением Sп, отстоящего от участка с меньшим сечением на расстоянии х. Температура нагрева сечений, ограничивающих участок dx, соответственно равна : ![]()
Тогда количество тепла, входящего в элемент dx за время dt, равно:
![]() (19)
(19)
а выходящего из него за время dt:
![]() (20)
(20)
Оставшееся при этом в элементе dx за время dt количество тепла будет равно:
![]() (21)
(21)
Оно суммируется с теплом dQ2, выделенным в элементе dx при прохождении по токопроводнику тока высокой частоты:
![]() (22)
(22)
Полученное элементом dx тепло частично идет на его нагрев:
![]() (23)
(23)
а частично отдается им в окружающую среду:
![]() , (24)
, (24)
в результате тепловой баланс элемента dx имеет вид:
![]() . (25)
. (25)
После подстановки вместо dQ их выражений, проведения преобразований и учета зависимости сопротивления от температуры, получим следующее дифференциальное уравнение второго порядка для температуры перегрева V суженного участка токопроводника:
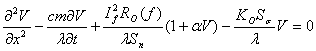 . (26)
. (26)
Оно описывает изменение температуры как по длине токопроводника х, так и по времени пропускания t тока высокой частоты.
Для ВВПК решение уравнения найдем для частного случая, когда требуется определить установившуюся температуру на расстоянии х от суженного участка. При этом максимальную температуру его примем одинаковой по всей длине. При установившемся режиме ![]() , а поэтому уравнение (26) принимает вид:
, а поэтому уравнение (26) принимает вид:
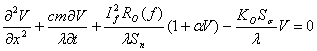 . (27)
. (27)
Частное решение уравнения (27) при ![]() позволяет определить установившуюся температуру перегрева Vy.np однородного токопроводника при отсутствии суженного участка:
позволяет определить установившуюся температуру перегрева Vy.np однородного токопроводника при отсутствии суженного участка:
![]() (28)
(28)
С учетом (28), общее решение уравнения (27) имеет вид:
![]() , (29)
, (29)
где Vc – х температура перегрева суженного участка, a![]() Из граничных условий при х = 1 и х = 0 находим, что C1= 0 и С2 = Vmах - Vy.np. После их подстановки выражение (29) принимает вид:
Из граничных условий при х = 1 и х = 0 находим, что C1= 0 и С2 = Vmах - Vy.np. После их подстановки выражение (29) принимает вид:
![]() (30)
(30)
По аналогии с выражением для максимальной температуры перегрева суженного участка Vmах при пропускании тока промышленной частоты выражение для Vmах применительно к току высокой частоты, после преобразования, принимает вид:
 (31)
(31)
где Sбс – площадь боковой поверхности, а Sc - поперечное сечение суженного участка. Преобразуем выражение (17) к следующему виду:
![]() . (32)
. (32)
После подстановки Ro(f) = ρ0L/П![]() и Sб = ПL в (32) и решения полученного равенства относительно периметра токопроводника П, получим следующее выражение для его расчета по заданному току высокой частоты при длине токопроводника 1 см:
и Sб = ПL в (32) и решения полученного равенства относительно периметра токопроводника П, получим следующее выражение для его расчета по заданному току высокой частоты при длине токопроводника 1 см:
 . (33)
. (33)
В соответствии с (33) величина тока определяется периметром токопроводника П, допустимой его температурой Ту.пр, температурой окружающей среды То и коэффициентом теплоотдачи Ко. Рассчитанные по (33) зависимости периметра для токопроводников длиной 1 см из меди, серебра, молибдена и бронзы БрБ2, по заданному току частотой 30 МГц при Ту.пр = 125 °С и То = 100 °С, приведены на рис.1.
Эти зависимости использованы для выбора диаметра D круглого, ширины h и толщины t плоского токопроводников созданных отечественных ВВПК. Указанные размеры могут быть рассчитаны и по следующим полученным в работе из (33) формулам:
 ; (34)
; (34) 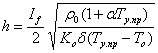 -
- ![]() , (если задана t) (35)
, (если задана t) (35)
 -
- ![]() , (если задана h). (36)
, (если задана h). (36)

Рис.1.Зависимость периметра токопроводника длиной 1 см, от тока частотой 30 МГц в вакууме при температуре теплорассеивающего элемента 100˚ С и нормальном давлении воздуха вокруг ВВПК
При задании отношения ширины к толщине n = h/t формулы для их расчета принимают вид:
 (37)
(37)  (38)
(38)
где ![]() удельное электрическое сопротивление материала токопроводника при температуре 20о С.
удельное электрическое сопротивление материала токопроводника при температуре 20о С.
Заключение
Полученные аналитические соотношения позволяют на этапе проектирования ВВПК по заданному току высокой частоты и рабочему напряжению рассчитать требуемые размеры токопроводящих элементов и контактного нажатия и оценить термический режим работы контактной группы ВВПК при пропускании заданного тока высокой частоты.
Список литературы:
1. Зарубин B. C. Инженерные методы решения задач теплопроводности. -М: Энергоатомиздат, 1983. – 328 с.
2. Камке Э. Справочник по обыкновенным дифференциальным уравнениям /Пер. с англ./. -М.: Наука, 1979. – 536 с.
3. Ким Е. И., Омельченко В. Т., Харин С. Н. Математические модели тепловых процессов в электрических контактах. – Алма-Ата: Наука, 1977. – 236 с.
дипломов


Оставить комментарий