Статья опубликована в рамках: IV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 20 сентября 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
КОМПЛЕКС ПРОГРАММ ДЛЯ РАСЧЕТА И МОДЕЛИРОВАНИЯ КОНСТРУКЦИИ ПЕРВИЧНОГО ПРЕОБРАЗОВАТЕЛЯ ДВУХКООРДИНАТНОГО МАГНИТОСТРИКЦИОННОГО НАКЛОНОМЕРА
Илюхин Кирилл Николаевич
студент 5 курса, ФИОТ, ПГТА, г. Пенза
Е-mail: Kirik.super@mail.ru
Зюзина Елена Григорьевна
студентка 5 курса, ФИОТ, ПГТА, г. Пенза
Е-mail: lena_412@mail.ru
Ермолаев Николай Александрович
научный руководитель, канд. тех. наук, доцент. каф. «Информационные технологии и системы» ПГТА, г. Пенза
Воронцов Александр Анатольевич
научный руководитель, аспирант каф. «Электроника и электротехника» ПГТА, г. Пенза
В настоящее время в промышленности для измерения углов наклона объекта относительной горизонтальной или вертикальной плоскости применяются различные виды наклономеров. По ряду основных параметров: точности, разрешающей способности, стоимости, наибольший интерес вызывают ультразвуковые магнитострикционные приборы. Их принцип действия основан на явлениях продольной магнитострикции, проявляющиеся через эффекты Видемана и Виллари.
Различают однокоординатные и двухкоординатные наклономеры. Один из вариантов последней группы, описан в [1] и представлен на рисунке 1.
Он содержит магнитострикционный преобразователь перемещений, выполненный в виде сферического корпуса 1 из немагнитного материала, например пластика, с заполненной наполовину рабочей жидкостью 2, поплавковым элементом 3 с кольцевым постоянным магнитом, называемого также поляризатором 4, однотипными С-образными звукопроводами 5, 6 из магнитострикционного материала [2]. Для изготовления опытного образца и запуск его в серийное производство, необходим предварительный расчет параметров элементов конструкции. Поэтому целью данной статьи является создание программы, учитывающей как конструктивные особенности элементов конструкции, а также их массу, размеры и материалы.
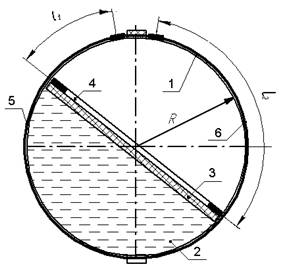
Рисунок 1. Первичный преобразователь двухкоординатного магнитострикционного наклономера.
Так как, с увеличением расстояния от звукопровода до поляризатора происходит резкое уменьшение напряженности магнитного поля, создаваемого поляризатором (П), то возникает необходимость в расчете и создании такой конструкции, где это расстояние было бы минимально. Данное условие выполняется при условии, что ![]() , где
, где ![]() — диаметр поляризатора, а
— диаметр поляризатора, а ![]() — радиус сферического корпуса. Это будет возможно, если ПЛ (поляризатор) будет располагаться симметрично относительно горизонтали, проведенной через центр сферического корпуса.
— радиус сферического корпуса. Это будет возможно, если ПЛ (поляризатор) будет располагаться симметрично относительно горизонтали, проведенной через центр сферического корпуса.
Для расположения ПЛ (поляризатора) над поверхностью рабочей жидкости (РЖ) необходимо, чтобы средняя плотность поплавкового элемента(ПЭ) и поляризатора была меньше плотности РЖ (рабочей жидкости).
Плотность РЖ (рабочей жидкости) определится по формуле:
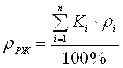 (1)
(1)
где ![]() и
и ![]() — процентное содержание и плотность парциальной жидкости, входящей в состав РЖ (рабочей жидкости).
— процентное содержание и плотность парциальной жидкости, входящей в состав РЖ (рабочей жидкости).
Для расширения областей применения наклономера, РЖ (рабочая жидкость) должна обладать следующими свойствами:
1. Большой коэффициент вязкости для гашения колебаний, возникающих от поплавкового элемента (ПЭ) с ПЛ (поляризатором) при изменении угла наклона.
2. Иметь малый коэффициент расширяемости и сжимаемости, что необходимо для работы в большом диапазоне температур.
3. При наличии нескольких жидкостей, они должны быть смешивающимися.
Так как в справочных данных указывают массу и габаритные размеры поляризатора, то вычисление средней плотности поляризатора и поплавкового элемента будет осуществляться по формуле:
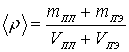 (2)
(2)
где ![]() и
и ![]() — массы поплавкового элемента и поляризатора, а
— массы поплавкового элемента и поляризатора, а ![]() и
и ![]() — их объемы.
— их объемы.


а) б)
Рисунок 2. Сферический корпус, содержащий поляризатор, поплавковый элемент а) цилиндрической формы и б) в виде шарового слоя, а также рабочую жидкость
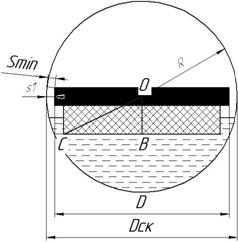
Рисунок 3. Сферический корпус. Поясняющий рисунок
Так как корпус первичного преобразователя будет сферическим, то для обеспечения минимального расстояния от поляризатора до звукопровода возможно использование кольцевого или дискового поляризатора.
Для расчетов объема для кольцевого и дискового поляризатора воспользуемся следующими формулами:
![]() (3)
(3)
![]() (4)
(4)
где ![]() и
и ![]() — высота, внешний и внутренний диаметры поляризатора соответственно. Выбор радиуса сферического корпуса R будем осуществлять из условия (см. рисунок 3)
— высота, внешний и внутренний диаметры поляризатора соответственно. Выбор радиуса сферического корпуса R будем осуществлять из условия (см. рисунок 3) 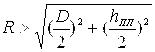 , откуда его диаметр
, откуда его диаметр![]() определится по формуле:
определится по формуле:
![]() (5)
(5)
Также необходимо учитывать изменение объема рабочей жидкости, возникающее вследствие температурного расширения или сжимаемости жидкости, с учетом которого неравенство (5) запишется следующим образом:
![]() (6)
(6)
где: ![]() ,
,
![]() — рабочий диапазон изменения температур,
— рабочий диапазон изменения температур,
![]() — коэффициент объемного расширения жидкости, являющийся справочной величиной.
— коэффициент объемного расширения жидкости, являющийся справочной величиной.
Так как расстояние s1 вдоль горизонтальной линии симметрии сферического корпуса от поляризатора до звукопровода согласно рисунку 2 ![]() , то учитывая формулу (6) получаем:
, то учитывая формулу (6) получаем:
 (7)
(7)
Минимальное расстояние Smin определится по формуле
 (8)
(8)
Радиус ПЭЦФ ![]() согласно рисунку определится по теореме Пифагора из
согласно рисунку определится по теореме Пифагора из ![]() неравенством:
неравенством:  , откуда его диаметр
, откуда его диаметр ![]() будет рассчитан по формуле:
будет рассчитан по формуле:
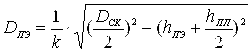 (9)
(9)
Значение диаметра ![]() ПЭСШ, согласно рисунку 1 б, выбираем равным внешнему диаметру D поляризатора, то есть
ПЭСШ, согласно рисунку 1 б, выбираем равным внешнему диаметру D поляризатора, то есть ![]() .
.
Диаметр ПЭЦФ должен выбираться из условия ![]() для кольцевого и
для кольцевого и ![]() для дискового поляризатора соответственно.
для дискового поляризатора соответственно.
Расстояние от звукопровода до поляризатора также зависят от глубина погружения в рабочую жидкость поплавкового элемента, что в свою очередь зависит от формы и размеров последнего, а также материала, из которого он изготовлен. Объем и масса поплавкового элемента диаметром ![]() и высотой
и высотой ![]() , указанных на рисунках 2 и 3 определится по формулам (10) — (13) соответственно:
, указанных на рисунках 2 и 3 определится по формулам (10) — (13) соответственно:
1. для поплавкового элемента цилиндрической формы (ПЭЦФ):
![]() (10) ;
(10) ; ![]() (11)
(11)
2. для поплавкового элемента в виде шарового слоя (ПЭШС):
 (12)
(12)
 (13)
(13)
соответственно, где ![]() — плотность поплавкового элемента, являющаяся справочной величиной. В качестве материала для изготовления поплавковых элементов отечественными и зарубежными компании, такие, как «Сенсор», “Baluff”, ОВЕН, Temposonics и другие используют эбонит, фторопласт, нержавеющие стали и т. д..
— плотность поплавкового элемента, являющаяся справочной величиной. В качестве материала для изготовления поплавковых элементов отечественными и зарубежными компании, такие, как «Сенсор», “Baluff”, ОВЕН, Temposonics и другие используют эбонит, фторопласт, нержавеющие стали и т. д..
Таким образом, объединяя формулы (1—4) и (9—13) определяем условие, при котором дисковый (14) и (16) и кольцевой (15) и (17) поляризаторы будут располагаться над поверхностью рабочей жидкости.
1. для ПЭЦФ:
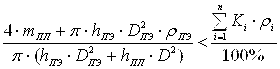 (14)
(14)
 (15)
(15)
2. для ПЭШС:
 16)
16)
 (17)
(17)
Из формул (1—4) и (9—13) следует, что средняя плотность поляризатора и поплавкового элемента будет вычисляться по формулам:
1. для дискового и кольцевого поляризатора с использованием ПЭЦФ соответственно:
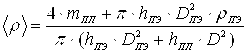 (18) и
(18) и  (19)
(19)
2. для дискового и кольцевого поляризатора с использованием ПЭШС соответственно:
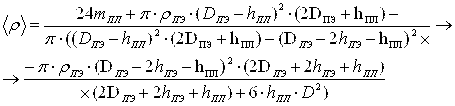 (20)
(20)
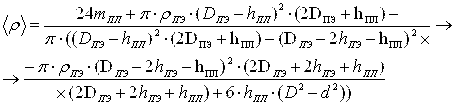 (21)
(21)
Расчет глубины погружения ![]() для ПЭЦФ и ПЭШС будет осуществляться по формулам (17) и (18) соответственно:
для ПЭЦФ и ПЭШС будет осуществляться по формулам (17) и (18) соответственно:
 (22)
(22)
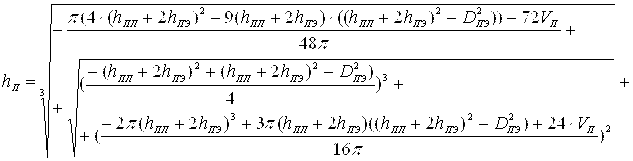
 (23)
(23)
где ![]() — объем части поплавкового элемента, погруженной в рабочую жидкость, для ПЭЦФ и ПЭШС определяемые по формулам (24) и (25) соответственно:
— объем части поплавкового элемента, погруженной в рабочую жидкость, для ПЭЦФ и ПЭШС определяемые по формулам (24) и (25) соответственно:
![]() (24)
(24)
 (25)
(25)
Выведем формулу для расчета объема рабочей жидкости, необходимой для достижения минимального расстояния между поляризатором и звукопроводом.
Объем рабочей жидкости найдем, вычитая из полученного объема шарового сегмента ![]() объем части поплавкового элемента
объем части поплавкового элемента ![]() , погруженного в рабочую жидкость.
, погруженного в рабочую жидкость.
![]() (26)
(26)
Объем шарового сегмента ![]() высотой
высотой ![]() определится по формуле где
определится по формуле где ![]() — радиус сферического корпуса.
— радиус сферического корпуса.
![]() (27)
(27)
Высота ![]() , согласно рисунку 2, определится по формуле:
, согласно рисунку 2, определится по формуле:
![]() (28)
(28)
Решая совместно уравнения (20—28) получаем формулу для расчета объема рабочей жидкости ПЭЦФ и ПЭШС соответственно:
![]() (29)
(29)
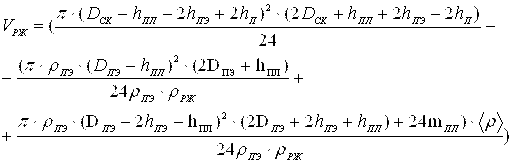 (30)
(30)
где: ![]() — диаметр сферического корпуса первичного преобразователя.
— диаметр сферического корпуса первичного преобразователя.
Исходя из всего написанного ранее, авторами статьи был разработана программа по расчету конструкции первичного преобразователя «Расчет ДМН», экранная форма которого приведена на рисунке 4.
В ней в качестве поплавкового элемента рассматривались ПЭ, изготовленные из пробки и пенопласта марки М35. В качестве рабочей жидкости использовалась смесь, состоящая из 80 % глицерина и 20 % спирта.

Рисунок 4. Экранная форма программы по расчету первичного преобразователя ДМН.
Результаты расчетов, полученные программно для различных диаметров поляризаторов и сферических корпусов что при выборе сферического корпуса диаметром менее 50 мм расстояние между звукопроводом и поляризатором достигает 5 % от внешнего диаметра, что свидетельствует о необходимости его выбора при расчетах исходя из условия ![]() >50 мм. При увеличении диаметра это значение уменьшается. Также стоит отметить, что значительное увеличение диаметра позволяет уменьшить это отношение, но и способствует увеличению массы как поляризатора, так и ДМН в целом. Как показывают результаты моделирования программы, наиболее приемлемым для моделирования автор видит выбор диаметра сферического корпуса в интервале 90—120 мм, что отображено в таблицах 1 и 2.
>50 мм. При увеличении диаметра это значение уменьшается. Также стоит отметить, что значительное увеличение диаметра позволяет уменьшить это отношение, но и способствует увеличению массы как поляризатора, так и ДМН в целом. Как показывают результаты моделирования программы, наиболее приемлемым для моделирования автор видит выбор диаметра сферического корпуса в интервале 90—120 мм, что отображено в таблицах 1 и 2.
Таблица 1
Входные данные программы «Расчет ДМН»
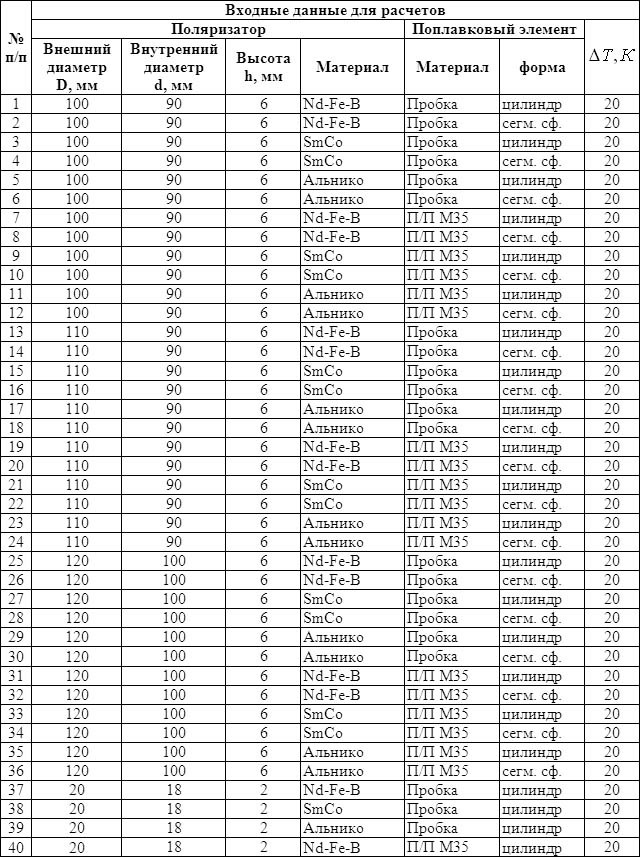
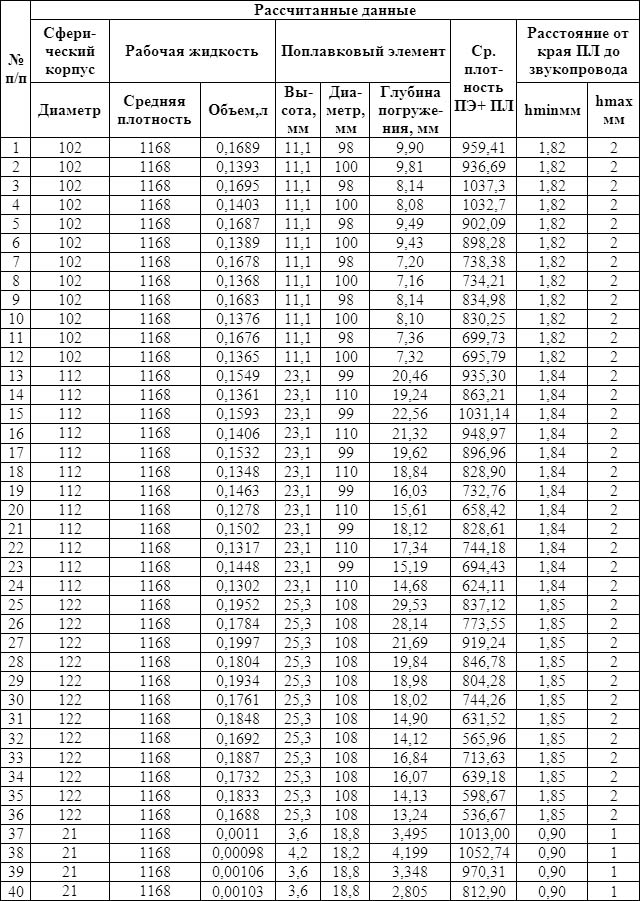
Таблица 2
Выходные данные программы «Расчет ДМН»
Список литературы:
1. Воронцов А.А., Демин С.Б, Демин Е.С. Магнитострикционный двухкоординатный наклономер. Патент РФ № 2389975. МПК: G01C9/18. Бюл. № 14, 2010. — 10 с.
дипломов



Оставить комментарий