ПОВЫШЕНИЕ ДАВЛЕНИЯ ВОДЫ В ТРУБЕ ПРИ ЕЁ ЗАМЕРЗАНИИ ВБЛИЗИ ГРАНИЦЫ

Калимуллин Ильдар Рашитович

студент 4 курса, физико-математический факультет, БФ БашГУ, г. Бирск

Е-mail: ild.kalimullin@mail.ru

Шагапов Владислав Шайхулагзамович

научный руководитель, д-р физ.-мат. наук, профессор, БФ БашГУ, г. Бирск

Значение льда трудно недооценить. Лёд оказывает большое влияние на условия обитания и жизнедеятельности растений и животных, на разные виды хозяйственной деятельности человека. Покрывая воду сверху, лед играет в природе роль своего рода плавучего экрана, защищающего реки и водоемы от дальнейшего замерзания и сохраняющего жизнь подводному миру. Если бы плотность воды увеличивалась при замерзании, лед оказался бы тяжелее воды и начал тонуть, что привело бы к гибели всех живых существ в реках, озерах и океанах, которые замерзли бы целиком, превратившись в глыбы льда, а Земля стала ледяной пустыней, что неизбежно привело бы к гибели всего живого.

Вода, попавшая летом в трещины, зимой замерзает и расширяет их; следующим летом количество воды в трещине увеличивается, и в результате с годами образуются клиновидные ледяные жилы, ширина которых достигает нескольких метров, а глубина — десятков метров. Часто давление льда и незамерзшей воды приподнимает вышележащий грунт, и возникает бугор вспучивания. Иногда грунт прорывается, вода выходит на поверхность и, замерзая, образует наледь. Эти процессы сильно осложняют строительство и эксплуатацию зданий и дорог, приходится принимать меры для сохранения мерзлого грунта в естественном, природном состоянии. С этой целью ставят здания на опоры, прокладывают охлаждающие трубы и др.

В процессе эксплуатации технических устройств в различных температурных режимах работы, используемых например в нефтегазодобыче, строительстве, могут возникнуть аварийные ситуации, связанные с образованием льда в замкнутых системах [4, с. 73]. Это объясняется повышением давления жидкости, так как при ее замерзании происходит уменьшение плотности.

В работе рассмотрена радиально-симметричная задача о замерзании воды в емкости (трубе) при охлаждении через стенки.

При математическом описании процесса теплопереноса уравнение теплопроводности для льда и жидкости имеет вид [2, с. 233]:

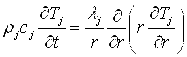,                                       (1)

где:  — плотность,

 — теплопроводность,

 — теплоемкость и  — температура среды,

 — (лед, жидкость).

Для жидкости запишем уравнение неразрывности и линейное уравнение состояния [3, с. 215]:

,                                  (2)

,                          (3)

где  — скорость и давление жидкости, нижний индекс 0 здесь и далее соответствует начальным значениям параметров жидкости,

 — коэффициент теплового расширения жидкости,

 — коэффициент сжимаемости, определяемый скоростью звука в жидкости .

В начальном состоянии (t = 0) жидкость имеет температуру T_l0, давление p₀. С некоторого момента времени на границе с координатой  начинает поддерживаться постоянная температура T_e, которая ниже температуры замерзания жидкости T_s, на оси симметрии емкости  выполняется условие отсутствия тепловых потоков .

На границе между жидкостью и льдом r = r_(s) температура равна температуре образования льда T_i = T_l = T_s , а также выполняются условия теплового баланса и баланса массы:

,  ,                       (4)

где:  — удельная теплота замерзания жидкости.

Линейное уравнение состояния (3) с учетом уравнения неразрывности (2) и теплопроводности (1) примет вид:

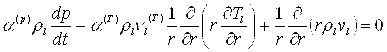,                           (5)

где: .

После интегрирования уравнения (5) по координате с учетом граничного условия и считая, что ,  получим:

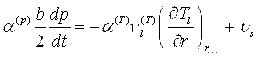
Скорость  выражаем из условия баланса массы (4):

,

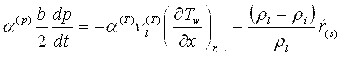.                 (6)

С другой стороны, из условия баланса тепла (13):

,

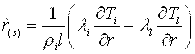подставляя в (6), получаем:

.

Уравнение, описывающее процесс повышения давления в воде, будет определяться равенством:

      (7)

В уравнении (7) первое слагаемое правой части отвечает за термическое расширение, второе — сжатие слоем льда.

Система уравнений (1)–(4),(7) решена методом конечных разностей [4, с. 131]. Разностные аналоги вышеперечисленных дифференциальных уравнений решены методом итераций с применением неявной четырехточечной разностной схемы.

При выполнении численных расчетов использовались следующие параметры [5]: , , , , , , , , , .

На рис. 1 иллюстрируется эволюция давления воды в зависимости от объема емкости, который определяется значением радиуса емкости b.

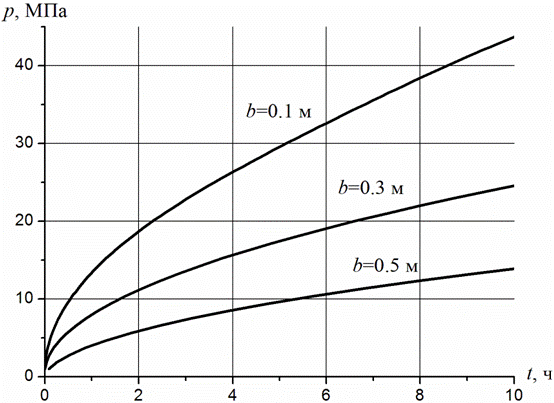
Рисунок 1. Зависимость давления от времени при различных значениях полуширины емкости b

На рис. 2 линиями 1, 2, 3 представлены зависимости температуры от координаты в различные моменты времени t = 1, 5, 10 ч соответственно при полуширине емкости .

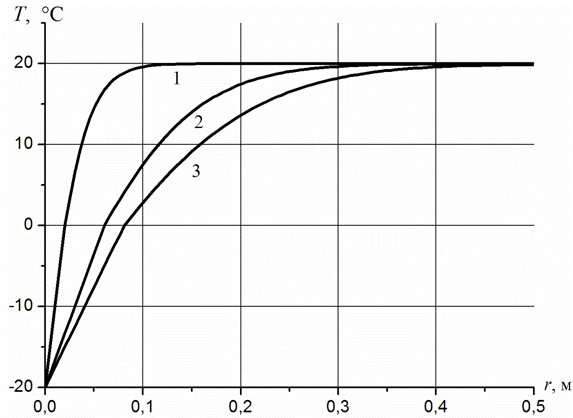
Рисунок 2. Распределение температуры по координате r

Получено аналитическое решение для радиально-симметричной задачи, позволяющей оценить величину повышения давления в трубе при заданных начальных и граничных условиях.

Список литературы:

1.Бабичев А.П., Бабушкина Н.А., Братковский А.М. Физические величины. Справочник. М.: Энергоатомиздат, 1991. 1232 с.

2.Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.

3.Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987. Ч. 1. 464 с. Ч. 2. 360 с.

4.Паундер Э. Физика льда. М.: Мир, 1967. 188 с.

5.Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.