Статья опубликована в рамках: XVIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 20 февраля 2013 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РАСЧЕТ ТЕМПЕРАТУРНЫХ ПОЛЕЙ В ОТРЕЗНОМ ИНСТРУМЕНТЕ
Прохоров Александр Владимирович
канд. техн. наук, филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет) в г. Озерске, г. Озерск Челябинской области
CALCULATION OF TEMPERATURE FIELDS IN THE CUTTING TOOL
Prokhorov Alexander
candidate of technical Sciences, Branch of Federal State State-Financed Educational Institution of Higher Professional Education «South Ural State University» (national research university) in Ozersk, Ozersk of Chelyabinsky region
АННОТАЦИЯ
В статье рассматриваются вопросы аналитического расчета температурных полей в дисковом отрезном инструменте. Проведен расчет температур для стального и вулканитового отрезного кругов.
ABSTRACT
The article deals with the analytical calculation of temperature fields in the disk cutting tool. The calculation of the temperature for steel and vulcanite cutting discs.
Ключевые слова: моделирование; теплопроводность; инструмент; отрезной круг.
Keywords: modeling; thermal conductivity; a tool; a cutting wheel.
На практике часто возникает необходимость определения температурного режима тел, непосредственное измерение температуры которых связано с техническими и методическими трудностями [1, с. 7]. В этом случае представляет практический интерес аналитический метод расчета тепловых процессов, основанный на создании моделей нагреваемых тел и источников.
Традиционно при создании таких математических моделей и построении температурных полей использовались либо численные методы [3], либо суперпозиция точечных источников теплоты [2, с. 10]. Развитие вычислительной техники и сопутствующего программного обеспечения позволяет применять при расчетах более сложные модели и аналитические приближения [6]. В настоящей работе предлагается математическая модель температурных процессов в дисковых телах при их нагреве внутренними источниками тепла, основанная на тезисах, развитых под руководством Пашацкого Н.В. в работах [4, 5, 9], посвященных проблематике приповерхностного нагрева твердых тел. Методика построения модели нагрева дисковых тел внутренними источниками тепла описана в работе [8] на примере электроэрозионной резки твэлов.
При разработке модели были сделаны следующие допущения [8]: теплоотвод с периферийной поверхности дискового тела не учитывается (толщина диска много меньше его радиуса), свойства материала не зависят от температуры (отсутствие фазовых переходов — плавления и испарения материала диска), источники тепла расположены равномерно по окружности дискового тела (это обеспечивается относительно быстрым вращением отрезного инструмента).
С учетом указанных допущений нестационарный процесс теплопроводности описывается дифференциальным уравнением в частных производных для цилиндрических координат:
 .
.
Граничные и начальное условия принимаются следующими:
Функция внутренних источников тепла взята в виде [8]:
где: n учитывает степень смещенности источников тепла к периферии диска.
В результате решения уравнения теплопроводности методом Фурье получено выражение для расчета температурных полей в дисковом теле с учетом сосредоточения источников тепла в периферийной области:
Здесь приняты следующие обозначения: ![]() — температура;
— температура; ![]() — радиус дискового тела;
— радиус дискового тела; 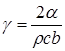 ;
; ![]() — толщина дискового тела;
— толщина дискового тела; ![]() — теплоемкость, плотность, температуропроводность материала соответственно;
— теплоемкость, плотность, температуропроводность материала соответственно; ![]() — коэффициент теплоотдачи с боковой поверхности диска;
— коэффициент теплоотдачи с боковой поверхности диска; ![]() — время;
— время; ![]() — корни функции Бесселя первого порядка
— корни функции Бесселя первого порядка ![]() ;
; ![]() — функция Бесселя нулевого порядка;
— функция Бесселя нулевого порядка; ![]() связано с количеством тепла
связано с количеством тепла ![]() соотношением:
соотношением:
 ,
,
где: t — время подвода тепла.
Для отрезных вулканитового и стального дисков, у которых рабочей (режущей) поверхностью является периферия диска, показатель n должен быть бесконечно большим. Однако, как показали расчеты в пакете MathCad, уже при n>50 температура периферии слабо изменяется с увеличением n. Расчет температурных полей проводился при следующих параметрах: ![]() Дж,
Дж, ![]() м,
м, ![]() м,
м, ![]() с, n=58. Для вулканитового диска были взяты значения
с, n=58. Для вулканитового диска были взяты значения ![]() Дж/(кг×К),
Дж/(кг×К), ![]() кг/м3,
кг/м3, ![]() м2/с; для стального отрезного диска —
м2/с; для стального отрезного диска — ![]() Дж/(кг×К),
Дж/(кг×К), ![]() кг/м3,
кг/м3, ![]() м2/с.
м2/с.
Расчеты температурных полей для вулканитового отрезного диска показали, что с увеличением времени температура на периферии диска неравномерно возрастает и при t=500 c наступает квазистационарное состояние, при котором температура поверхности практически не изменяется и к этому моменту при ![]() Вт/(м2×К) достигает величины около 500°С. Вследствие плохой теплопроводности материала наблюдается резкий спад относительной температуры при уменьшении r, и при r=0,067 м (
Вт/(м2×К) достигает величины около 500°С. Вследствие плохой теплопроводности материала наблюдается резкий спад относительной температуры при уменьшении r, и при r=0,067 м (![]() ) она близка к нулю.
) она близка к нулю.
Анализ температурных кривых на рисунке 1 показывает, что при отсутствии конвекции относительное приращение температуры периферии вулканитового диска достигает 1700°С (кривая 1), что может привести к разрушению инструмента. Кроме того, в отсутствие конвекции расширяется область высоких температур режущем слое. При введении вынужденной конвекции температура периферии значительно снижается, доходя при ![]() Вт/(м2×К) до 100°С (кривые 2 и 3). Использование материала с большими теплопроводящими свойствами (например, стали) также приводит к существенному снижению температуры на периферии (сталь на рисунке представлена кривыми 4 и 5).
Вт/(м2×К) до 100°С (кривые 2 и 3). Использование материала с большими теплопроводящими свойствами (например, стали) также приводит к существенному снижению температуры на периферии (сталь на рисунке представлена кривыми 4 и 5).
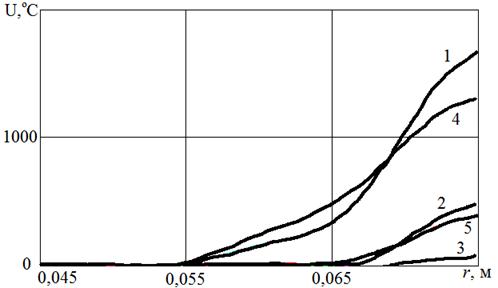
Рисунок 1. Зависимость температуры от интенсивности теплоотдачи: 1 — ![]() , 2 — 50, 3 — 500 Вт/(м2×К), t=500 c; 4 —
, 2 — 50, 3 — 500 Вт/(м2×К), t=500 c; 4 — ![]() , 5 — 50 Вт/(м2×К), t=500 c
, 5 — 50 Вт/(м2×К), t=500 c
Указанная методика расчета температурных полей может быть расширена на другие дискообразные тела с некруглой геометрией режущей кромки и, как следствие, с иным распределением приповерхностных источников тепла (дисковые фрезы, стальные дисковые пилы и др.).
Список литературы:
1.Кулаков М.В. Измерение температуры поверхности твердых тел / М.В. Кулаков, Б.И. Макаров. — М.: Энергия, 1979. — 96 с.
2.Кутателадзе С.С. Основы теории теплообмена / С.С. Кутателадзе. — Новосибирск: Наука, 1970. — 416 с.
3.Осовец С.В. Расчет нестационарного теплового состояния плиты при ее нагреве перемещающимся источником / С.В. Осовец, Е.В. Торопов, А.В. Прохоров, В.Л. Кириллов // Инженерно-физический журнал. — 2000. — Т. 73, № 4. — С. 757—760.
4.Пашацкий Н.В. Тепловые процессы при сварке плоских изделий / Н.В. Пашацкий, А.В. Прохоров // Сварочное производство. — 2000. — № 7. — С. 3—5.
5.Пашацкий Н.В. Тепловые процессы при обработке предварительно нагретой стальной плиты огневой машиной / Н.В. Пашацкий, А.В. Прохоров // Известия ВУЗов. Черная металлургия. — 2001. — № 3. — С. 46—48.
6.Прохоров А.В. Теплопроводность и массообмен в системах с приповерхностными источниками: дис. канд. техн. наук / А.В. Прохоров. — Озерск, 2003. — 122 с.
7.Пашацкий Н.В. Нагрев лезвия проходного резца / Н.В. Пашацкий, А.В. Прохоров, В.В. Закураев, А.А. Шивырев // СТИН. — 2003. — № 4. — С. 21—23.
8.Пашацкий Н.В. Расчет температурных полей дискового электрода при электроэрозионной резке материалов / Н.В. Пашацкий, А.В. Прохоров, В.Ф. Обеснюк // Сварочное производство. — 2003. — № 8. — С. 37—41.
9.Пашацкий Н.В. Аналитический расчет распределения температур при многопроходной сварке дисковых деталей / Н.В. Пашацкий, А.В. Прохоров, С.Н. Кононов // Сварочное производство. — 2006. — № 3. — С. 3—6.
10.Резников А.Н. Теплофизика резания / А.Н. Резников. — М.: Машиностроение, 1969. — 288 с.
дипломов


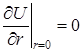

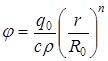
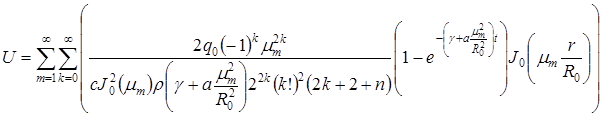
Оставить комментарий